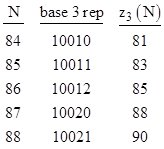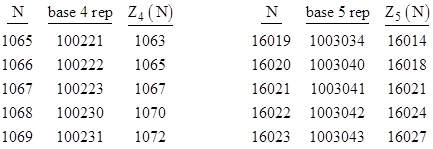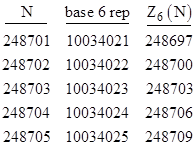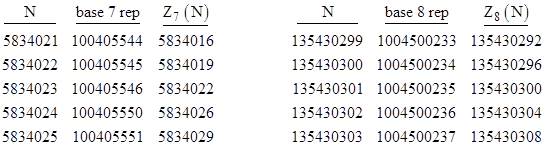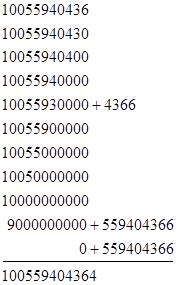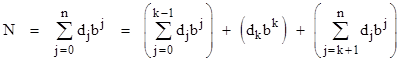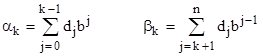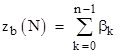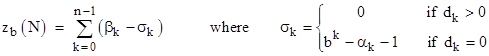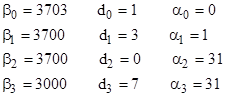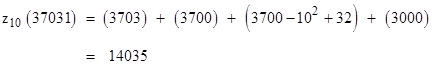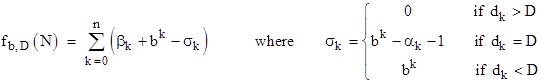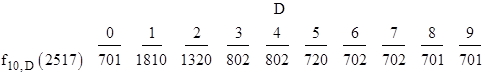Counting Zeros and Crossing Over

I don’t entirely resign.  I may teach the third Gospel

this afternoon.  I haven’t made up my mind.

                                                         John Berryman

Let z_b(N) denote the total number of “0” digits in the base-b representations of the natural numbers from 1 to N (inclusive). For any given b, does there exists a number N such that z_b(N) = N? Clearly with b=2 this condition is satisfied by N=8, because the first eight natural numbers written in binary are 1, 10, 11, 100, 101, 110, 111, 1000, and the total number of “0” digits in these numbers is 8.

In general, for any given b, as we step through the natural numbers, each digit will equal 0 with an asymptotic frequency of 1/b, so the rate of increase of z_b(N) is roughly proportional to the number of digits of N. As a result, z_b(N) initially grows more slowly than N, but eventually grows faster (as the number of digits increases), so it is certain to cross over at some point near N ≈ b^b+1. However, this doesn’t guarantee a solution of z_b(N) = N, because near the cross-over point the value of z_b(N) is typically increasing by more than 2 as N increases by 1, so it may jump from below to above N without ever equaling N. For example, with b=3 there is no solution, because the values near the cross-over point are as shown below.

If we let Z_b(N) denote the total number of “0” digits in the base-b representation of the natural numbers from 0 to N (instead of 1 to N), then Z_b(N) = z_b(N) + 1, and so N = 86 is a solution of Z₃(N) = N. The next few bases also have solutions of Z_b(N) = N but not of z_b(N) = N, as shown in the tabulations below of the cross-over points.

The next two bases have no solution for either the z or the Z function, as can be seen in the tabulation below.

What about the base 10? To answer this, we first look more closely at how the value of z_b(N) can be efficiently computed. This is a well-known exercise for computer programmers, usually accomplished by simply adding the numbers of integers up to N that contain a “0” in the kth digit. For example, the number of integers less than decimal 37231 that contain a “0” in the least significant digit is equal to the number of integers of the form “X0” where X is any sequence of digits from 1 to 3723, so we have 3723 of these. The number that contain “0” in the second least significant digit is equal to the number of integers of the form “X0Y” where X is any sequence of digits from 1 to 372, and Y is any digit from 0 to 9, so we have 3720 of these. Likewise the numbers that contain “0” in the third least significant digit are of the form “X0Y” where X is any sequence of digit from 1 to 37, and Y is any sequence of two digits from 00 to 99. Thus we have 3700 of those numbers. And so on. It follows that the number of zeros in the decimal representations of the integers from 1 to 37231 is 3723 + 3720 + 3700 + 3000 = 14143. This works for any N that contains no zeros.

A slight complication arises when N contains a zero. For example, suppose N = 37031. The integers from 1 to N that contain a “0” in the third least significant digit (where the “0” appears in N itself) are of the form “X0Y”, and if X is any sequence of digits from 1 to 36 then Y can be any sequence of two digits from 00 to 99. However, if X = 37, the possible values of Y are restricted to the range 00 to 31, because in that case we are considering numbers of the form “370Y”, so Y cannot exceed 31. So, the number of integers from 1 to N with “0” in the third least significant digit is 3600 + 32 = 3632. Thus the number of zeros in the decimal representations of the integers from 1 to 37031 is 3703 + 3700 + (3600+32) + 3000 = 14035.

To illustrate this technique, consider the number of zeros in the decimal representations of the integers from 1 to 100559404365. To compute z₁₀(N) we simply sum the values

Since Z₁₀(N) = z₁₀(N) + 1, we see that N = 100559404365 is a solution of Z₁₀(N) = N. In summary, we’ve seen that there is a solution of Z_b(N) = N for b = 2, 3, 4, 5, 6, and 10, but not for b = 7 or 8. (We haven’t examined b = 9.)

One way of formalizing the calculation of z_b(N) is by partitioning the base-b representation into three parts. Letting d_j denote the jth digit of N, we can write

where k is any integer from 0 to n−1, with the understanding that the first expression in parentheses on the right side is zero for k = 0. If we define the quantities

(with the stipulation that α₀ = 0) and if none of the digits of N are zero then we have simply

On the other hand, if we allow for N to have some zero digits, the full expression for z_b(N) is

In our previous example, with b = 10, N = 37031, and n = 4, we had

Thus the formula gives

as expected. For a related discussion, see the note on Geometric Dot Products and Digit Reversals.

Naturally the same reasoning as discussed above can be used to evaluate the number of occurrences of any non-zero digit D in the base-b representations of the integers up to N, which we will denote as f_b,D(N). The main difference is that leading occurrences of non-zero digits are counted, so the summation must be carried out for k = 0 to n, and we must consider the case when d_k < D. This leads to the formula

with the stipulation that β_n = 0. For example, the numbers of occurrences of the digits “0” to “9” in the integers from 1 to 2517 are

Of course, the sum of these numbers equals 9×1 + 90×2 + 900×3 + 1518×4 = 8961. Also, note that if 0 < α < β then f_b,β(N) ≤ f_b,α(N), and equality holds iff α and β have the same ‘greater than’ or ‘less than’ relationship to each of the digits of N.

Return to MathPages Main Menu