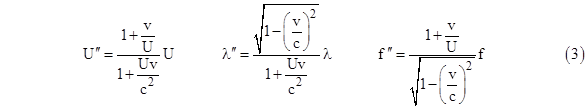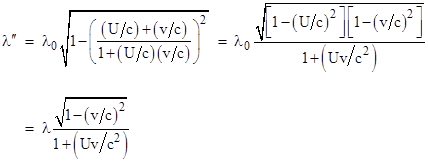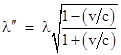Different Wavelengths

Our soul is cast into a body, where it finds number, time, dimension. Thereupon it reasons, and calls this nature necessity, and can believe nothing else.

                                                                                                      Pascal, 1670

Let S denote a system of inertial coordinates, i.e., a system of space and time coordinates x,t in terms of which the isotropic equations of Newtonian mechanics hold good, at least quasi-statically, and consider a wave (or regular sequence of pulses) emanating from a source at rest in S. This wave could be an acoustic sound wave, a light wave, a water wave, or any other kind of wave. Let U, λ, and f denote the speed, wavelength, and frequency of the wave in terms of S. By definition we have U = fλ (There is no ambiguity if we stipulate either ballistic pulses with characteristic speed U relative to the source, or else a wave in a medium at rest in S.)

Now consider a receiver moving with speed v directly toward the source of the wave. Let Uʹ, λʹ, and fʹ denote the speed, wavelength, and frequency of the wave in terms of a system of coordinates Sʹ in which the receiver is at rest, and such that S' is related to S by a Galilean transformation xʹ=x+vt, tʹ=t. Again by definition we have Uʹ = fʹλʹ, and we can easily verify that

These relations are exact for any values of U and v. In particular, they apply to light waves with U = c, where c denotes the speed of light in vacuum. In that case we have

But we can just as well define another system of coordinates, S", in which the receiver is at rest, but such that S" is related to S by a Lorentz transformation xʺ=(x+vt)γ, tʺ=(t+vx/c²)γ where γ=[1−(v/c)²]^−1/2. Letting Uʺ, λʺ, and fʺ denote the speed, wavelength, and frequency of the wave in terms of these coordinates, we have Uʺ = fʺλʺ where

If U and v are both small in comparison with c, then equations (3) are essentially the same as equations (1). However, if the speed U of the wave approaches c, the differences between (1) and (3) become significant. In the case of a light wave, we have U=c, and equations (3) become

These relations differ both qualitatively and quantitatively from equations (2). For example, according to equations (2) the wavelength is invariant and the speed of light is c+v in terms of Sʹ, whereas according to equations (4) the speed of light is invariant and the wavelength is contracted by the inverse of the frequency factor in terms of Sʺ.  It's worth noting that although the frequencies given by (2) and (4) differ only at the second order in v/c, the speeds and wavelengths differ at the first order. 

Which of these descriptions is correct?  The answer is that both are perfectly correct. They describe exactly the same events, merely expressed in terms of two different coordinate systems Sʹ and Sʺ. The receiver is at rest in terms of both of these coordinate systems. Remember that we stipulated the original coordinate system S is an inertial coordinate system, in the sense that the isotropic equations of Newtonian mechanics hold good (at least quasi-statically) in terms of those coordinates, but we did not stipulate that Sʹ or Sʺ were inertial coordinates. Instead, we specified that Sʹ is related to S by a Galilean transformation, and Sʺ is related to S by a Lorentz transformation. As a matter of empirical fact, Sʺ is an inertial coordinate system, and Sʹ is not. By convention and tradition, inertial coordinates are usually regarded as the “true” measures of space and time, so equations (3) are regarded as the “true” speed, wavelength, and frequency of a wave that propagates at any speed U, and in particular this gives (4) for a wave that propagates at the speed U = c.

Much of the confusion over this point is due to the unfortunate fact that there are two different definitions of "inertial coordinate system" in common usage, one that requires only Newton's first law to be satisfied, and another that requires all three of Newton's laws to be satisfied. The inadequacy of the first definition is made clear by the preceding example, because both Sʹ and Sʺ are inertial coordinate systems in the sense of the first definition, but only S" is an inertial coordinate system in the sense of the second definition. Newton’s third law of equal action and reaction is satisfied (at least quasi-statically) in terms of Sʺ, but not in terms of Sʹ. This doesn’t mean that Sʹ is an invalid system of coordinates, but it does mean that we cannot apply Newton’s isotropic equations of mechanics in Sʹ without also introducing fictitious forces (just as we must do when we describe phenomena in terms of a rotating coordinate system). The mistake of anti-relativityists who espouse equations (1) and (2) is not that those equations are “wrong” for Sʹ (they are actually correct), but that they implicitly assume that Sʹ is an inertial coordinate system, in the full sense of the term, which it is not.

When confronted with this explanation, the anti-relativisyist is typically dis-satisfied. Why, he asks, are inertial coordinate systems related by Lorentz transformations rather than Galilean transformations? In particular, why are the planes of simultaneity of relatively moving systems of inertial coordinates skewed relative to each other? The answer is that all forms of energy – including kinetic energy – have inertia. (This corresponds to the fact that E = mc².) This is the key fact that is absent from Newtonian mechanics. Since kinetic energy is frame dependent, and kinetic energy has inertia, it follows that inertia is frame dependent, and hence any synchronization based on inertial isotropy must be frame dependent. The recognition of energy, in all its forms, as a real palpable thing, is what makes Lorentz invariance unavoidable, and implies that inertial coordinate systems must be related by Lorentz transformations with their skewed planes of simultaneity. Of course, this doesn’t imply that we must describe events in terms of inertial coordinate systems. Some people (such as Lorentz) have argued that it is more satisfying to use systems of coordinates that all share the same time coordinates, i.e., that are related by Galilean transformations, so that “one can speak of simultaneity without further specification”. However, this view is inherently hypocritical, since it still requires one to specify the chosen time coordinates in physically meaningful terms, and in practice this is invariably done by selecting a convenient system of inertial coordinates. The tacit assumption that we are free to make this choice, and then apply the isotropic laws of physics (without fictitious forces) to these coordinates, is tantamount to adopting inertial coordinates as the most natural measures of space and time.

Sometimes beginning students in relativity theory question the expression for the wavelength given in (4), because they naively expect that the lengths of the wave in terms of the two coordinate systems moving at relative speed v to be related by what is presented in some elementary texts as the length contraction factor [1 – (v/c)²]^1/2. But that is a simple misunderstanding, because that factor relates the length of an object in its rest frame to the length of the object in a relatively moving frame. (Bear in mind that we define the length of an object for any given system of coordinates as the spatial distance between the end points at the same time coordinate.) In the case we are discussing, the wave is not at rest in either frame. In general, if two successive crests of a wave (or sequence of ballistic pulses) are moving at speed U in terms of S, and if λ₀ is the spatial distance between those crests in terms of the inertial coordinate system in which the wave is at rest (which certainly exists for any U < c), then the wavelength in terms of S is indeed given by the naive contraction factor

The speed of the wave in terms of Sʺ, the system of inertial coordinates in which the receiver is at rest, is given by the first equation in (3), so we can apply the naive contraction factor to give the wavelength in terms of Sʺ as

Therefore, in the limit as U goes to c, we have

in agreement with (4).

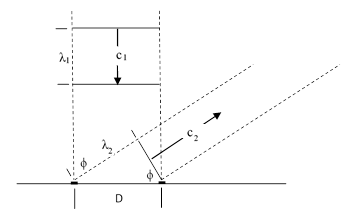
Incidentally, one might think that the annual Doppler effect for stars in the ecliptic plane, as measured by a diffraction grating, provides direct observational proof that the wavelength of light is different for different states of motion of the receiver. However, this is obviously not true. If it were true, we could combine such a wavelength measurement with the frequency (which we can certainly measure, at least for sufficiently low frequencies) to provide an unambiguous measurement of the one-way speed of light without any stipulation of simultaneity. This doesn’t work because a diffraction grating provides an unambiguous measure of the wavelength only if we stipulate that the incident speed of light equals the refracted speed of light, which is not to be expected in an emission theory. (See, for example, Pauli’s 1921 treatise on relativity for comments on the ambiguity in the interpretation of diffraction gratings in a hypothetical emission theory.) In general, the angle of diffraction (for the primary fringe) can be inferred from the figure below.

Here c₁ and c₂ denote the speeds of the incident and diffracted waves respectively. The wavelength of the incident wave is λ₁ and of the refracted wave if λ₂, where the latter equals (c₂/c₁)λ₁. The primary fringe occurs at the angle ϕ such that sin(ϕ) = λ₂/D, so we have

Thus if we know that c₂ = c₁ = c, then we can say λ₂ = λ₁ = λ and sin(ϕ) = λ/D. However, in this context we do not know, a priori, that the speed of light is invariant. For example, in an emission theory of light we may expect the refracted light to have the characteristic speed c, but the incident light may have some different speed c₁ = fλ₁ where f is the given frequency of the light and we are trying to decide if the Doppler shift is due to a change in speed or a change in wavelength. If the Earth is moving toward a distant star with speed v, then a neo-Newtonian emission theory for a given frequency f might say c₁ = c + v and c₂ = c, giving a diffraction angle satisfying sin(ϕ) = (λ₁/D)/(1 + v/c). To the first order, this gives the same angle as in special relativity, although according to special relativity the speed of light is c and the wavelength of the incident light is not λ₁ but rather λ₁/(1 + v/c). Thus a diffraction grating does not give a direct measurement of wavelength if we do not stipulate the invariance of the speed of light, so it can’t be used to distinguish between an emission theory and special relativity. (This is true even if we overcome the effects of extraneous extinction due to the Earth’s atmosphere and interstellar gas, etc., because the diffraction itself represents complete extinction). We should qualify these comments by noting that diffraction itself is problematic for emission theories, so we must make some charitable allowances to even make the comparison. Still, these considerations show that observations of the annual Doppler shift do not represent direct and unambiguous measurements of either wavelength or speeds. The actual emperical basis of special relativity (in addition to the direct measurements, e.g., Alvager, 1964, showing that light speed is independent of the motion of the source) consists of all the experimental confirmations of the inertia of energy, which directly implies that inertial coordinate systems (in the full sense) are related by Lorentz transformations.

Prior to special relativity, most people had a naive conception of space and time, unsupported by any epistemological foundations. They didn't appreciate how our ideas of space and time are based on the phenomena of our experience. Instead, they naively accepted certain high-level conceptual frameworks, such as Euclidean geometry and Galilean spacetime, as a priori elements of thought. One lesson of relativity was that we can't take the metric of either space or spacetime for granted, nor can we assume any a priori structure. We must establish a clear connection between our ideas about space and time and physical phenomena. A careful examination of phenomena led to the discovery of the inertia of energy, which implies Lorentz invariance, which leads to the Minkowskian metric of spacetime as an efficient encoding of the universal effects due to Lorentz invariance. Unfortunately, instead of gaining an appreciation for the epistemological foundations of kinematics and dynamics (and even geometry), most people simply adopted the Minkowskian spacetime just as naively as they had previously accepted Galilean spacetime. In other words, they simply switched allegiances from one naive camp to another. This is why most arguments between anti-relativityists and pro-relativityists are so pointless, because in most such arguments none of the participants understand the basis and justification for their beliefs. Both sides suspect that the other side doesn’t really understand the issues, and they are both right.

To be fair, much of the confusion can be traced back to the way in which relativity was historically introduced and taught. The main problem was (and is) failure to recognize the operational definition of simultaneity already implicit in Newtonian mechanics, based on inertial isotropy and the law of equal action and reaction. This obscures the solid empirical foundation of the theory, and leaves some beginning students with the impression that special relativity is nothing but a set of postulated tautologies with no physical content. Also, the delayed appearance of mass-energy equivalence as a consequence of special relativity, rather than as it’s foundational basis, tends to obscure the underlying motivation for the theory. It would be more satisfactory to take the physically plausible empirical fact (inertia of energy) and then explain why this implies that the speed of light has the same value in terms of relatively moving systems of inertial coordinates, rather than taking the latter proposition as a postulate and deducing the inertia of energy.

Return to MathPages Main Menu