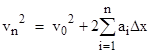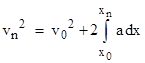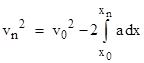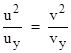Refraction Revisited and Newton’s Gespensterfeld

One of the most intriguing episodes in the history of science is the story of how the “sine law” of optical refraction was discovered and rationalized by various theoreticians. It’s remarkable that the same law of refraction is consistent with seemingly incompatible conceptions of the propagation of light. According to the conceptions of Descartes and Newton the law implies that light propagates more rapidly in denser media, whereas according to the conceptions of Fermat and Huygens the same law implies that light propagates more slowly in denser media.

The “sine law” consists of the fact that, for light rays passing through a plane boundary between two given transparent media, the ratio of the sines of the angles of incidence and refraction (relative to a line perpendicular to the surface) is constant. There is some evidence that this “law” was known to Thomas Harriot around 1602, but he never published it. Johannes Kepler, who had corresponded with Harriot, wrote about refraction in 1611, but didn’t present the sine law. Willebrord Snell is usually credited with the discovery, but didn’t publish it either.

Rene Descartes was the first to publish the sine law, and he also presented a derivation of this law from his principles of physics. Unfortunately, Descartes’ reasoning was somewhat incoherent, since he contended that light propagates instantaneously and yet he “explained” refraction by analogy to the velocity components of a tiny projectile passing through a membrane at the boundary between the two media. He argued that the force (or determination) of light pressure follows the same rules as velocities of moving particles. This is a dubious proposition (even if light were an instantaneous pressure, which of course it is not), and his reasoning relied on other dubious premises as well, many of which were pointed out by Pierre Fermat in 1637.

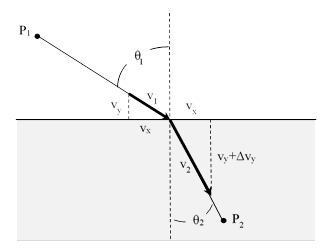
A more coherent explanation of refraction, with some similarity to that of Descartes but based consistently on the projectile model of light, was later given by Newton in Proposition 95 of Book 1 of his Principia (1686), and also in Proposition 6 of Book 1 of his Opticks (1704, but based on his studies in the 1670’s). Newton’s idea was that light behaves as if composed of tiny ballistic corpuscles, and that there are forces of attraction or repulsion between those particles and the material media through which they pass. If a corpuscle of light is moving in a homogeneous and isotropic medium, the forces exerted on the corpuscles will be isotropic (the same in all directions), and therefore the corpuscle will continue by the law of inertia to move at uniform speed in a straight line. However, near the boundary between two media of different densities, the situation is not isotropic, and one expects that there would be a net force on a corpuscle of light in the direction perpendicular to the surface of the boundary. This would cause the speed in the perpendicular direction to increase (when entering a more dense medium) while the transverse speed would remain unchanged, as shown in the figure below.

Newton was equivocal as to why the corpuscle would be accelerated at it entered the denser medium. At times he argued that each corpuscle is subject to a short-range attraction to the substances comprising the media, and is more attracted to denser media. Near the boundary there will be a net attraction toward the denser medium, so the corpuscle will accelerate as it crosses the boundary. At other times Newton speculated that there might exist an aether, and this aether might be more dense in regions of space devoid of ordinary matter, and less dense in regions where ordinary matter is present. This aether might then be thought to impel the corpuscles of light from the region of greater density and pressure to the region of less density and pressure.

Regardless of the cause, Newton supposed that the corpuscles crossing the boundary were subjected to a force perpendicular to the boundary, from which it follows that

The speeds of light v₁ and v₂ in the two media are fixed (for any given pair of media), so the ratio of sines is fixed. Thus Newton has “explained” Snell’s law, based purely on the supposition “that bodies refract light by acting upon its rays in lines perpendicular to their surfaces”. Also, the empirical fact that the angle of refraction is reduced when passing into a denser medium implies (according to this model) that the speed of light is greater in a denser medium. Hence the force on the corpuscles as they cross the boundary must be directed toward the denser medium.

Newton actually gave a more detailed account of refraction (and reflection), by considering the thin region near the boundary, with a finite force being applied over a non-zero distance. In this discussion he asserted the following proposition:

If any motion or moving thing whatsoever be incident with any velocity on any broad and thin space terminated on both sides by two parallel planes, and in its passage through that space be urged perpendicularly towards the farther plane by any force which at given distances from the plane is of given quantities, the perpendicular velocity of that motion or thing, at its emerging out of that space, shall be always equal to the square root of the sum of the square of the perpendicular velocity of that motion or thing at its incidence on that space, and of the square of the perpendicular velocity which that motion or thing would have at its emergence, if at its incidence its perpendicular velocity was infinitely little.

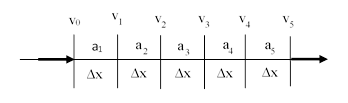
He doesn’t present a proof of this, saying “The demonstration mathematicians will easily find out, and therefore I shall not trouble the reader with it”. Being not as considerate as Newton, we shall trouble the reader with the demonstration. Only the perpendicular motion is involved in this proposition, so without loss of generality we can consider motions in a single dimension. Consider a corpuscle of light entering a region on the left with speed v0 and passing through a series of small regions of width ∆x, in each of which the force (and hence the acceleration) has some arbitrary constant value, as shown below.

For each segment we have the relations

Squaring the expression for v_i, we have

Therefore, given n segments of size ∆x in which the accelerations are a₁, a₂, ..., a_n, we have

In the limit as the spatial increments ∆x go to the infinitesimal dx, the summation can be written as an integral of the acceleration function a(x), so we have

Now, for the hypothetical corpuscle with initial speed u₀ = 0, the square of the exit speed u_n is simply given by the integral term, so we have Newton’s result

Newton also asserted that “the same proposition holds true of any motion or thing perpendicularly retarded in its passage through that space, if instead of the sum of the two squares you take their difference”. This takes some interpretation, because the second square is defined as the speed that a corpuscle would have when it exits the region, given that it has zero speed at the beginning of the region. But if the force in that region acts to retard passage through that space, such a particle would never progress into the space at all, let alone reach the other side. So, to make sense of this assertion, we must either assume that the hypothetical corpuscle is still subjected to a force urging it forward, and only the actual particle is being subjected to a retarding force, of the same magnitude at each point, or else we must assume that the hypothetical corpuscle enters the segment at the opposite end, and exits the segment at the point where the actual particle enters. In either case, we can prove the assertion by simply negating the accelerations a_i in the demonstration above, leading to

where “a” is the magnitude of the retarding acceleration, and then we identify the integral term with the square of the exit speed for a hypothetical particle with initial speed 0 after passing through the region of acceleration. We can do this unambiguously because the sequence in which we encounter the incremental slices doesn’t affect the resulting speed. Thus we arrive at Newton’s expression v_n² = v₀² – u_n² for the case of a retarding force.

Incidentally, notice that if the retarding force is great enough, or the region of deceleration is thick enough, an incident ray striking a surface obliquely will not penetrate the region, but will be turned around, and will exit on the same side that it entered, with the same transverse speed (which is unaffected) and reverse perpendicular speed. Hence the angle of reflection equals the angle of incidence, so Newton’s model gives the correct angular law of reflection as well as refraction.

There is a certain plausibility to Newton’s reasoning. We know that the transverse speed of a particle bouncing obliquely off a surface is unaffected, and only the perpendicular speed is changed. Also, if we imagine a corpuscle of light moving first in one homogeneous and isotropic region, and then passing a boundary into another homogeneous and isotropic region, and that the corpuscle responds mainly to short-range forces between itself and the surrounding medium, it is not entirely unreasonable to suppose that the only time when there is a net force on the corpuscle is when it passes through the boundary region, where the short-range conditions are not isotropic. Furthermore, the anisotropy is purely in the direction perpendicular to the boundary. We still have symmetry in the transverse directions. Hence it is not unreasonable, in the context of a particle theory of theory, to suppose that the transverse component of the corpuscle’s speed is unaffected, and only the perpendicular component of the speed is altered. When it is found that this supposition leads to the correct sine law for refraction, it seems to have even more plausibility. Thus Newton remarked

This demonstration being general, without determining what light is, or by what kind of force it is refracted, or assuming any thing farther than that the refracting body acts upon the rays in lines perpendicular to its surface, I take it to be a very convincing argument of the full truth of this proposition.

However, as noted above, Fermat had already criticized the somewhat similar reasoning of Descartes in 1637, and twenty years later Fermat returned to the subject and proposed a completely different way of understanding refraction. Around 1657 Fermat’s attention was drawn to the fact that the paths of light obeying the law of reflection, i.e., with equal angles of incidence and reflection, are the shortest paths from the source to the destination by way of the reflecting surface. Of course, the usual straight-line paths of light moving directly from one place to another are also the shortest possible paths, since that is a defining property of a straight line. Fermat was impressed by this, and suspected that it might be possible to derive the law of refraction by simply finding the “shortest” paths – but of course this doesn’t work for spatial measures, because the path of a refracted ray is not spatially straight, i.e., it is not the shortest spatial path from emitter to receiver.

Fermat’s great inspiration was the idea that perhaps the actual governing principle is not for the path to go the least distance, but for it to take the least time. This principle of least time would still apply to direct motion, and to reflection, because in those cases the path of least distance is also the path of least time, since the speed of light is fixed in those circumstances. But for refraction, we may suppose that the speed of light is different in different media, and if so, the path of least time will not be spatially straight. Lacking the apparatus of calculus, it was not trivial for Fermat to work out the exact paths, but he eventually succeeded, and discovered to his surprise that the ratio of the sines of the angles of incidence and refraction was constant (for two given media), exactly as in the theory of Descartes and Newton. However, despite this striking agreement, on a deeper level Fermat’s account of refraction was fundamentally different because instead of equation (1) it led to the relation

Thus, where Newton’s equation has the velocities, Fermat’s equation has the reciprocals of the velocities. To be consistent with the empirical fact that the angle of refraction is reduced for denser media, Fermat’s equation implies that the speed of light must be reduced when entering a denser medium, which is the exact opposite of Newton’s conclusion. Indeed by combining equations (1) and (2) we have the relation

where the subscripts N and F denote Newton and Fermat. This shows that the product of the predicted speeds of light for Newton and Fermat’s models is constant, and since we can imagine that every ray of light passed at some point through vacuum, where Newton and Fermat agree that the speed of light is the constant c, then it follows that for all conditions

This is intriguing, because it has exactly the same form as the relationship between the phase velocity and the group velocity of a matter wave in quantum theory, and also for electromagnetic signals propagating in a wave guide. It’s tempting to wonder if the velocity of Newton, and the “determination” or instantaneous pressure of Descartes, actually do correspond to some physically meaningful quantity.

Experiments have shown that the ordinary phase velocity of light matches the velocity in Fermat’s equation rather than Newton’s, and this has usually been taken as proof that Newton and Descartes were simply mistaken, a conclusion that was reinforced by the success of the wave model of Huygens, et al, which gives results consistent with Fermat’s principle and forms the basis of modern optics. Nevertheless, there is a sense in which Newton’s corpuscle conception of light, or at least his skepticism of the naive classical wave model, was partially vindicated by quantum field theory, and it’s interesting to consider whether the Newtonian speed v_N has any physical significance. For example, a pulse of light propagating in a medium with speed less than c possesses a well-defined rest frame and therefore an effective mass, so one might consider viewing it as a matter wave with distinct phase and group speeds.

On the other hand, the group speed of a matter wave is below c and the phase speed is above c, whereas the phase speed of a refracted light ray in a dense medium is below c. Thus if we were to interpret Newton’s speed as a group speed, we would need to invoke some mechanism (e.g., anomalous dispersion) to account for the group speed being above c.

Recall that the governing principle of Newton’s model is that the transverse speed of light is unaffected when passing through a plane boundary between two media. In other words, letting v denote the velocity of the incident ray and u denote the velocity of the refracted ray, and letting x denote the perpendicular direction and y denote the transverse direction, Newton says that u_y = v_y, whereas we can show that Fermat’s model implies u_y/u² = v_y/v², which can also be written as

This is the velocity that is held constant across the boundary. The numerators are the squared speeds of light in the respective media, and the denominators are the transverse components of the ordinary phase velocities in those media.

Fermat’s model turned out to be correct (at least in terms of the ordinary phase velocity), and indeed his “principle of least time” was the first application of a variational principle to physics, an approach that has proven to be immensely useful and far-reaching. However, it was initially greeted with skepticism, as in this comment from Clerselier, a supporter of Descartes:

The principle you take as a basis for your proof, to wit, that nature always acts by the shortest and simplest path, is only a moral principle, not a physical one—it is not and can not be the cause of any effect in nature.

We also note that Fermat’s derivation based on minimizing the integral of n(v)ds would give the same angular result regardless of the postulated relationship between the index of refraction n and the velocity of light v in a given medium. Newton’s mechanistic model implied n(v) = v/c, whereas Fermat assumed n(v) = c/v, but Fermat would have arrived at the same sine law had he selected any other function of velocity for n(v), including Newton’s, and then minimized the integral of n(v)ds, provided only that n is a constant for any given medium. Subsequently Christain Huygens developed a wave model of light, which gave a plausible mechanistic explanation for why light (usually) propagates in conformity with Fermat’s principle of least time, and also was able to account for various interference phenomena.

Incidentally, to account for interference phenomena in his corpuscular theory, Newton found it necessary to hypothesize a hybrid wave/particle theory, as follows:

Every ray of light in its passage through any refracting surface is put into a certain transient constitution or state, which in the progress of the ray returns at equal intervals... Nothing more is requisite for putting the rays of light into fits of easy reflection and easy transmission than that they be small bodies which by their attractive powers, or some other force, stir up vibrations in what they act upon, which vibrations being swifter than the rays, overtake them successively, and agitate them so as by turns to increase and decrease their velocities, and thereby put them into those fits.

This is strangely similar to Einstein’s speculations in the 1920’s about a ghost field (“Gespensterfeld”) associated with each photon, guiding it along its path in such a way as to account for the interference probabilities. This would necessarily be a non-local field, corresponding to the fact that Newton’s ghost field needed to be “swifter than the rays”, i.e., super-luminal. Ironically, in his critique of the classical wave theory, focusing on the effects of what we now call polarization, Newton found that a similar ghost field would be needed. He wrote

It is difficult to explain by these [wave theory] hypotheses how rays can be alternately in fits of easy reflection and easy transmission, unless perhaps one might suppose that there are in all space two aethereal vibrating mediums, and that the vibrations of one of them constitute light, and the vibrations of the other are swifter [i.e., non-local], and as often as they overtake the vibrations of the first, put them into those fits. But how two aethers can be diffused through all space, one of which acts upon the other, and by consequence is re-acted upon, without retarding, shattering, dispersing, and confounding one anothers motions is inconceivable.

Evidently Newton thought the combination of two wave models was less intelligible than a particle model of light combined with a superluminal ghost wave.

Return to MathPages Main Menu