|
Stochastic Sprinkling |
|
|
|
The vacuum of empty space is evidently Lorentz invariant, in the sense that the simple homogeneous and isotropic expressions for the laws of dynamics to which all palpable phenomena conform are the same when those phenomena are described in terms of any two inertial coordinate systems, which are related by Lorentz transformations. Einstein noted that, although this does not preclude the existence of something that might be called an “ether”, such an ether could not consist of any material substance comprised of parts that can be tracked through time, because such an ether would have a definite velocity at any given event, and hence would not be Lorentz invariant. Some possible ways around this argument have been considered. For example, in the 1950’s Dirac suggested an ether consisting of a flux of particles with velocities in all directions at every point, and he argued that this could be Lorentz invariant if the velocity distribution was “uniform” from −c to +c in every direction. However, the distribution would have to be uniform in the Lorentzian sense, which implies that the density would have to go to infinity at the extreme velocities ±c. |
|
|
|
Another proposal for a relativistic ether is to imagine it comprised of individual events, which do not have trajectories in spacetime. An individual event in spacetime is indeed Lorentz invariant in the sense that it doesn’t distinguish a particular frame of reference or state of motion, but it does distinguish a position and time, so to be fully relativistic we must populate all of spacetime with events. If we imagine a continuous manifold of events with some uniform non-zero density, we get a scalar field, which is Lorentz invariant. However, a continuum has a huge number of degrees of freedom, whereas the success of quantum physics suggests that any finite system can be fully characterized by a finite amount of information, and the universe should have at most a countably infinite number of degrees of freedom. This leads us to consider whether spacetime itself could be ultimately a discrete structure with countable degrees of freedom. We might try to represent spacetime as a discrete set or lattice of events instead of a completed continuum. |
|
|
|
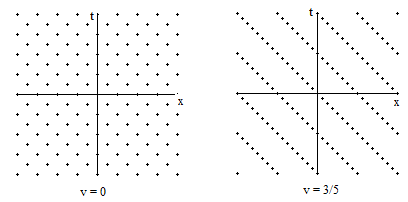
Clearly if we simply populate spacetime with a regular lattice of events, the lattice will not generally be Lorentz invariant. For example, consider the lattice of events in the x,t plane shown on the left below. |
|
|
|
|
|
|
|
The discrete events are placed at regular intervals of the null coordinates r = x + t and s = x – t. The effect of a Lorentz transformation for a velocity v in the positive x direction is to re-scale the r and s coordinates as rʹ = kr and sʹ = (1/k)s where k = [(1+v)/(1−v)]1/2. The right hand plot shows the same pattern of discrete points after being transformed with k = 2, corresponding to v = 3/5. Obviously this set of events is not invariant under Lorentz transformations, since we can easily distinguish between these two configurations. |
|
|
|
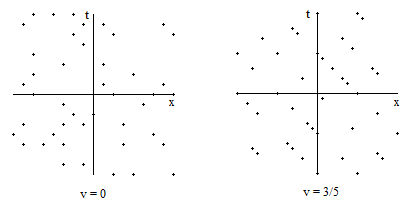
One way of trying to avoid this problem and recover Lorentz invariance is to select only a random sampling of the discrete events comprising the regular lattice. (Of course, the hypothesis that a perfectly random selection can be made is problematic in this context, since it implies a continuum for the range of the random variable, which must always remain conjectural at best.) This is sometimes called a stochastic sprinkling. To illustrate, suppose we take the same set of regular events as above, but we randomly select only one out of four events. In other words, for each event shown above, we toss an honest coin twice, and we include the event if and only if the coin comes up heads both times. This leads to the set of discrete events shown in the figure on the left below. |
|
|
|
|
|
|
|
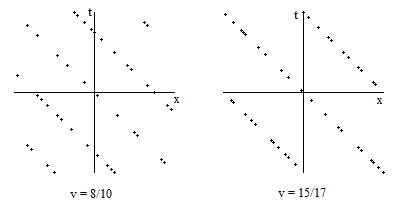
When we apply the same Lorentz transformation as before, with the factor k = 2, we get the distribution shown on the right hand figure. These two figures look roughly similar, and this similarity extends over the entire xt plane. So we might think this randomized selection of discrete events is Lorentz invariant. However, if we examine the same set of discrete events with boost factors of k = 3 and k = 4 (corresponding to velocities v = 8/10 and v = 15/17) we get the results shown below. |
|
|
|
|
|
|
|
As the boost becomes more extreme, we can see more clearly the lack of Lorentz invariance. Each time we double the boost factor, we double the density of the events along the diagonals, and double the distance between those diagonals, making them progressively more recognizable. Clearly for any given non-zero interval size and randomized density, we can increase the boost factor until the failure of Lorentz invariance becomes apparent. |
|
|
|
One might think that we could arrive at perfect Lorentz invariance by letting the interval size for the rs grid approach zero, but this is an example of the limit fallacy. The properties of the elements of a sequence need not be the same as the properties of the limit of that sequence. Again, for any non-zero “cell” size in the rs grid, no matter how small, Lorentz invariance manifestly fails at some sufficiently high boost factor. An array with a cell size equal to zero is the continuum, which is not a discrete structure. For another possibility, we could consider a non-zero cell size but with the selection of events within each cell with real-valued coordinates uniformly distributed within each cell. However, the use of real values with infinite precision represents the introduction of a continuum with infinite amounts of information in the coordinates of each discrete event. Thus if we restrict ourselves to configurations with countably infinite amounts of information, there does not exist a perfectly Lorentz invariant discrete structure for spacetime. |
|
|