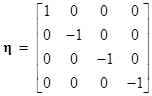Preserving the Intervals

In terms of Cartesian coordinates x,y,z, in flat three-dimensional Euclidean space, the squared length (magnitude) of any interval with the increments dx, dy, dz is

As discussed in the note on Bras, Kets, and Matrices, letting x and x^T denote respectively the column vector and row vector with the incremental components, we can write this as

where I is the identity matrix. (We could omit the identity matrix without affecting the result, but we include it here to show how it generalizes to other metrics later.) Now suppose we apply a linear transformation M to the x vector to give X = Mx. If we want M to represent a rotation, it must leave the magnitude of every vector unchanged, so we must have

Since this must be satisfied for every vector x, it follows that

Consequently if M is a rotation we have M⁻¹ = M^T. This is a necessary but not quite sufficient condition, because a reflection also satisfies this requirement. Recall that the determinant of a product of matrices equals the product of the determinants of the individual matrices, and that the determinant of a transpose equals the determinant of the original matrix. Therefore, taking the determinant of both sides of (2), we find |M|² = 1, which implies that the magnitude of |M| is unity, but doesn’t determine the sign. We distinguish between a rotation and a reflection by the fact that |M| = +1 for a rotation and |M| = −1 for a reflection. As discussed in the note on Eigenspaces, a pure reflection in three-dimensional space leaves invariant the points on one specific plane through the origin, and transposes the points on opposite sides of that plane.

Notice that in the above discussion the identity matrix I represents the metric coefficients defining the Pythagorean spatial line element (1). In special relativity the spacetime line element for rectilinear orthogonal coordinates t,x,y,z has the form

where τ is the proper time along the incremental world line. If we now let x denote the column vector with elements dt, dx, dy, dz, we can write (3) in the form

where

Now suppose we apply a linear transformation L to the x vector to give X = Lx. If we want L to represent a Lorentz transformation (which is a hyperbolic rotation in spacetime), it must leave the magnitude of every vector unchanged, so we must have

Since this must be satisfied for every vector x, it follows that

Consequently if L is a Lorentz transformation we have ηL⁻¹ = L^Tη. This is a necessary but not quite sufficient condition, because a reflection also satisfies this requirement. Taking the determinant of both sides of (4), we find |L|² = 1, which implies that the magnitude of |L| is unity, but doesn’t determine the sign. We distinguish between a restricted Lorentz transformation (i.e., combinations of rotations and boosts) and a reflection by the fact that |L| = +1 for a restricted Lorentz transformation and |L| = −1 for a reflection.

In general relativity we must deal with more general metric tensors, since there does not usually exist a global system of coordinates in terms of which the metric tensor equals η. In fact, the determinant of the metric tensor g need not be unity. In general we have the invariant line element

Just as in the previous cases, we could consider linear transformations that leave the magnitude of every line element unchanged while retaining the given metric tensor g. By the same reasoning as before, it’s clear that such a transformation, A, must satisfy the relation

which can also be written as gA⁻¹ = A^Tg.  However, since the metric g is allowed to be a function of the coordinates, the components of A would also be functions of the coordinates, so the coordinate transformation will be truly linear only in an infinitesimal region in which the metric coefficients are essentially constant.

Return to MathPages Main Menu