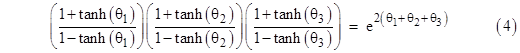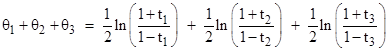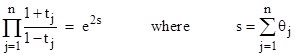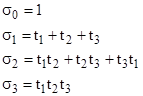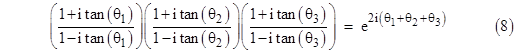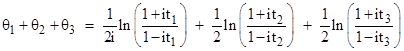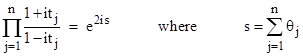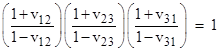Tangential Identities

To the first order, the expressions (1+x)/(1−x) and e^2x both equal 1+2x, although they differ at higher orders. This suggests that an interesting function might be definable in terms of these expressions. Indeed, the hyperbolic tangent can be defined implicitly by the relation

Solving for tanh(θ) yields the more usual definition

This is just the hyperbolic sine divided by the hyperbolic cosine. Putting t = tanh(θ) we have θ = inv tanh(t), and taking the natural log of both sides of equation (1) and dividing through by 2 we get the identity

Several other useful identities follow from these expressions. For example, given any three quantities θ₁, θ₂, θ₃, we see from equation (1) that

Taking the natural log of both sides and dividing through by 2, we have

where t_j denotes tanh(θ_j). If θ₁ + θ₂ + θ₃ = 0 then the right side of equation (4) equals 1, and we can clear the denominator and cancel terms to arrive at

More generally, given any n quantities θ₁, θ₂, ..., θ_n and the corresponding values t_j = tanh(θ_j), we have

Consequently, we can clear the denominator and re-arrange terms to give the identity

where σ_m is the mth elementary symmetric function of the quantities t_j. For example, with n = 3 the elementary symmetric functions are

We stipulate that σ_m = 0 for m > n. In terms of these quantities we have

In other words, the hyperbolic tangent of any sum of quantities equals the sum of the odd elementary symmetric functions of the hyperbolic tangents of those individual quantities divided by the sum of the even elementary symmetric functions. If we consider the n individual quantities as orthogonal coordinates, it’s interesting that this complicated function of the n coordinates in invariant throughout any (n-1)-dimensional subspace with a given sum, such as the diagonal planes in 3-dimensional space.

With n = 2 we have just two quantities θ₁, θ₂ and the corresponding quantities t_j = tanh(θ_j), from which we get σ₀ = 1, σ₁ = t₁ + t₂, and σ₂ = t₁t₂. The above relation then gives the familiar addition rule for the hyperbolic tangent

Analogously to equation (1), the usual tangent function is defined implicitly by the relation

Solving for tan(θ) we get the more usual definition

Putting t = tan(θ), we have θ = inv tan(t), and we can solve equation (5) for θ to give the identity

Given any three quantities θ₁, θ₂, θ₃, we see from equation (4) that

Taking the natural log of both sides and dividing through by 2i, we have

where t_j denotes tanh(θ_j). If θ₁ + θ₂ + θ₃ = kπ for any integer k, then the right side of (8) equals 1, and we can clear the denominator and cancel terms to arrive at

where t_j denotes tan(θ_j). On the other hand, if θ₁ + θ₂ + θ₃ = (k + 1/2)π for any integer k, then the right side of the relation equals −1, and we get

More generally, given any n quantities θ₁, θ₂, ..., θ_n and the corresponding values t_j = tan(θ_j), we have

Consequently, we can clear the denominator and re-arrange terms to give the identity

where σ_m is the mth elementary symmetric function of the quantities t_j. In terms of these quantities we have

This can also be written as

which shows that if s = kπ for any integer k, then the sum of the odd symmetric functions with alternating signs vanishes, whereas if s = (k + 1/2)π then the sum of the even symmetric functions with alternating signs vanishes.

Now consider three arbitrary quantities q₁, q₂, q₃ and let u_ij = q_i – q_j. It follows that

Putting θ₁ = u₁₂, θ₂ = u₂₃, θ₃ = u₃₁, and letting v_ij = tanh(u_ij) we see from equation (4) that we have the relation

Identifying the quantities v_ij as the speed of the spatial origin of inertial coordinate system i in terms of inertial coordinate system j, the quantities u_ij are called the rapidities, and the above expression gives the rule for velocity composition in special relativity.

Return to MathPages Main Menu