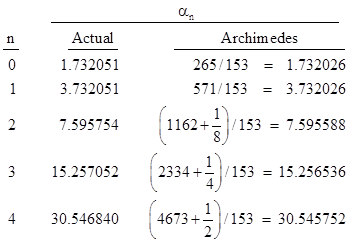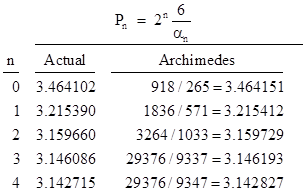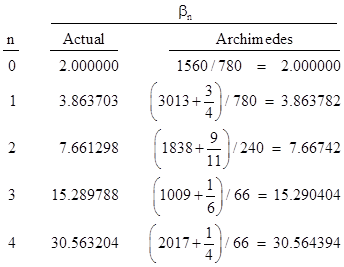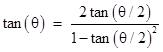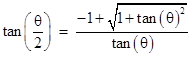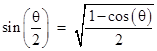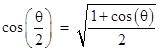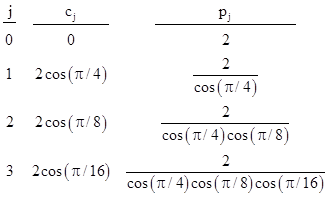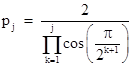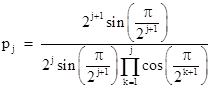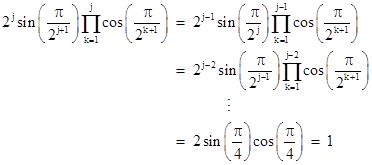Archimedes and Godfrey

To my daughter Leonora, without whose never-failing sympathy and encouragement this book would have been finished in half the time.

                                                                                      P. G. Wodehouse

The Greek mathematician Archimedes of Syracuse, around the year 250 BC, developed recursive formulas giving converging upper and lower bounds on the value of π, in terms of the perimeters of regular polygons, doubling the number of edges on each step of the calculation. Over 2000 years later, someone named John T. Godfrey of Punta Gorda, Florida, wrote a letter to the editor of BYTE magazine (May 1987), describing essentially the same method of calculating π, but with an interesting variation. Before describing Godfrey’s method, we’ll review the calculation of Archimedes.

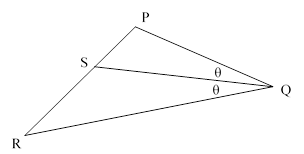
In his calculation, Archimedes made use of an elementary lemma (Proposition 3, Book VI of Euclid’s Elements) stating that for any triangle PQR, if a line through Q bisects the angle PQR and strikes the opposite edge PR at point S, then PS/SR = PQ/QR, as illustrated below.

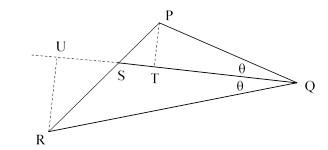
The proof is fairly immediate if we drop perpendiculars from P and R to points T and U on the (extended) bisecting line QS as shown below.

Since QTP and QUR are similar, we have PT/RU = PQ/RQ. Also, since RUS and PTS are similar, we have PS/RS = PT/RU = PQ/RQ, which was to be proven.

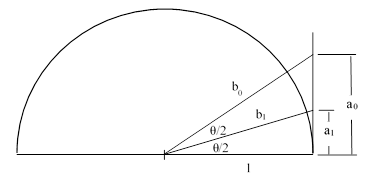
With this result in hand, we can describe Archimedes’ method for calculating upper and lower bounds on the value of π. The figure below was used by Archimedes to calculate the upper bound. Given half the edge length of a regular n-gon circumscribing a circle, it shows his construction of half the edge of a regular 2n-gon circumscribing the circle.

Given the values of α₀ = 1/a₀ and β₀ = b₀/a₀, we wish to compute the values of α₁ = 1/a₁ and β₁ = b₁/a₁. The Lemma implies that b₀ = (a₀ – a₁)/a₁, so it follows that α₁ = α₀ + β₀. Also, by Pythagoras’ Theorem, we have 1 + a₁² = b₁², and dividing through by a₁² gives α₁² + 1 = β₁². The same calculation could then be repeated, given the half edge length for a regular polygon circumscribing a unit circle, doubling the number of sides on each step. Thus Archimedes arrives at the recurrence

In modern trigonometric terms we recognize that α_j = 1/tan(θ/2^j) and β_j = 1/sin(θ/2^j), and the recurrence relations are simply the trigonometric identities

Half the perimeter of a regular n-gon circumscribing a unit circle is P_n = n tan(π/n), which is an upper bound on the value of π. Archimedes took a hexagon as his starting point, so his initial angle was θ = π/6 (= 30°), and hence a₀ = 1/√3 and b₀ = 2/√3, which gives the initial values α₀ = √3 and β₀ = 2 for the recurrence. Using an unspecified method for determining rational lower bounds on square roots (beginning with 265/153 for √3) Archimedes applied the recurrence (1) four times, giving progressively closer lower bounds for α_j, which will give upper bounds for π. If we carry out this calculation with high decimal precision and compare with Archimedes’ results, we get

The corresponding upper bounds on π, which we denote by P_n, are given by 2ⁿ(6/α_n), as summarized in the table below.

It’s interesting that the reduced numerators of Archimedes’ rational approximations for P₃ and P₄ are equal. Also, Archimedes noticed that his P₄ equals 3 + 1335/9347, and if the denominator of the fractional remainder is reduced by just 2 it equals 1335/9345 = 1/7, so he adopted the slightly less tight but more convenient upper bound 3 + 1/7  ≈  3.142857 for π.

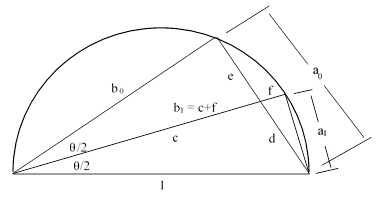
To find a lower bound on π, Archimedes considers regular polygons inscribed inside a circle with unit diameter. In this case each edge is a chord of the circle, such as the segment of length b₀, subtending the angle θ as shown in the figure below. (Note that Archimedes makes use of the well-known fact that triangles inscribed in a semi-circle on the diameter are right triangles, and that the angle subtended by a chord at a point on the perimeter of a circle is half the central angle. For the circumscribed case above he considered the full central angle of a half-edge, whereas for the inscribed case below he considers the half-angle for a full edge. As a result, the initial angle is π/6 in both cases.)

Given the values of α₀ = b₀/a₀ and β₀ = 1/a₀, we wish to compute the values of α₁ = b₁/a₁ and β₁ = 1/a₁. By similar triangles we have b₁/a₁ = b₀/e, and by the Lemma we have b₀ = e/d, and therefore b₁/a₁ = 1/d. This implies b₁/a₁ = (b₀+1)/(e+d) = (b₀+1)/a₀, so we have α₁ = α₀ + β₀. Also, by Pythagoras’ Theorem, we have a₁² + b₁² = 1, and dividing through by a₁² gives α₁² + 1 = β₁². Thus Archimedes arrives again at recurrence (1). Just as in the circumscribed case, we recognize that α_j = 1/tan(θ/2^j) and β_j = 1/sin(θ/2^j), and the recurrence relations are simply the trigonometric identities noted previously.

The perimeter of a regular n-gon inscribed in a circle with unit diameter is p_n = n sin(π/n), which is a lower bound on the value of π. Archimedes took a hexagon as his starting point, so his initial angle was θ = π/6, and hence his initial values for the recurrence were α₀ = √3 and β₀ = 2, just as in the circumscribed case. Again using his unspecified method for determining rational upper bounds on square roots (beginning with 1351/780 for √3) he applied the recurrence (1) four times, giving progressively closer upper bounds for β_j, which will give lower bounds for π. If we carry out this calculation with high decimal precision and compare with Archimedes’ results, we get

The corresponding lower bounds on π, which we denote by p_n, are given by 2ⁿ(6/β_n), as summarized in the table below.

In the light of modern trigonometry, a more natural way of computing the value of tan(θ/2) from the value of tan(θ) would be to simply make use of the identity

This gives

which can be applied recursively. Beginning with a convenient value, such as tan(π/4) = 1, this enables us to compute upper bounds on π by the expressions 2ⁿ tan(π/2ⁿ). Geometrically this corresponds to the half-perimeter lengths of regular 2ⁿ-gons circumscribed on a unit circle. Likewise we have lower bounds given by 2ⁿ sin(π/2ⁿ). We could use one of the well-known half-angle formulas for the sine, such as

but this involves the cosine function. The cosine can be expressed in terms of the sine, but this complicates the formula. Is there a simpler way? Notice that the cosine function has a simple half-angle formula in terms of itself, i.e.,

Multiplying through by 2, this can be written as

So, letting c_j denote 2cos(π/2^j+1) for j = 0, 1, 2, …, we see that these values satisfy the recurrence

Now suppose we define another sequence p_j with the initial value p₀ = 2 and the recurrence

Thus we have

This shows that the values of p_j can be expressed as

Multiplying the numerator and denominator of the right hand side by 2^j sin(π/2^j+1), we get

Making use of the identity sin(2x) = 2sin(x)cos(x), the denominator can be “telescoped” as follows:

Therefore, we have

so these are lower bounds converging on π. Also, recalling that c_j = 2cos(π/2^j+1), we can immediately form the sequence r_j = 2p_j/c_j = 2^j+1tan(π/2^j+1), so this gives the sequence of upper bounds. Conceptually these are identical to the calculations of Archimedes, but equations (2) and (3) differ slightly in appearance, so their equivalence may not be obvious. The latter equations were suggested by Godfrey’s letter to BYTE magazine, responding to an article that had appeared previously in that magazine. The previous article had mentioned only two ways of computing π, one by summing Gregory’s series π/4 = 1 – 1/3 + 1/5 – 1/7 + … (which of course is hopelessly slow), and the other using Machin’s formula. Both of these are purely algebraic, so they seem to have motivated Godfrey to think about a geometrical calculation based on polygons, just as Archimedes had done. It seems that Godfrey was unacquainted with ancient Greek mathematics, because he wrote that he had not seen any simple recursive formulas for computing upper and lower bounds on π in the literature. Even if he had seen Archimedes’ formulas, he might not have recognized them, since the equivalence is obvious only when the terms are expressed as trigonometric functions (which neither Archimedes nor Godfrey employed), and only if we recognize the telescoping. Aside from stating that his sequences are related to the perimeters of inscribed and circumscribed polygons, and that he had derived the recurrence using only algebra and Pythagoras’ Theorem, Godfrey didn’t give any explicit derivation. He also stated that a “suitable average” of the upper and lower bounds is given by (2p_j + r_j)/3, but he provided no indication of the sense in which this is the optimum weighting.

Return to MathPages Main Menu