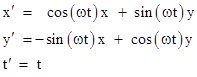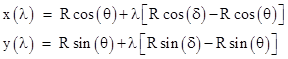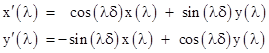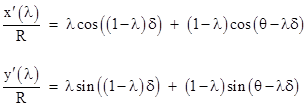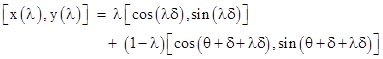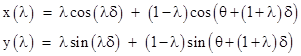Light Paths in Rotating Coordinates

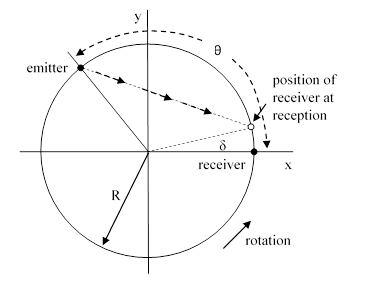
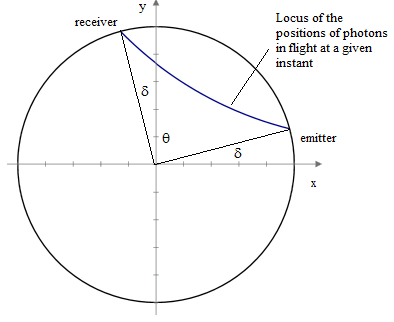
Consider an emitter and receiver attached to different points on the rim of a circular disk of radius R that is rotating about its central axis with constant angular speed ω. The axis is assumed to be at rest in an inertial coordinate system x,y,t, and we assume that the signal propagates at the invariant speed c = 1 in terms of those coordinates. Let θ denote the angle between simultaneous positions of the emitter and receiver, as shown below.

At the time t_e the receiver passes through the point (R,0) and the emitter passes through the point

At this instant the emitter emits a pulse of light, and this pulse (or photon) propagates through vacuum to the receiver, which has moved to the point

at the time of reception, due to the rotation of the disk during the time of flight. Since light propagates along null intervals, we know that

Inserting the expressions for the x and y coordinates of the emission and reception events, and noting that δ = ω(t_r – t_e), this implies

so for any values of ω, R, and θ we can solve for δ.

Needless to say, the light pulse (or photon) in vacuum and flat space-time follows a linear path in terms of any system of inertial coordinates (by conservation of momentum), but what is the shape of the light path in terms of a coordinate system x′, y′, t′ that is rotating along with the disk?  (For example, we might be interested in tracing the path on the disk surface along which the pulse travels from emitter to receiver as the disk rotates.) We choose coordinates given by the transformation

In this rotating system of coordinates the receiver’s position has the constant coordinates [R, 0], and the emitter has the constant coordinates [Rcos(θ), Rsin(θ)]. To determine the light path in terms of the rotating coordinates, we first note that the path from emitter to receiver in terms of the original inertial coordinates can be expressed with a parameter λ ranging from 0 to 1 as

Furthermore, setting t_e = 0, the value of ωt increases from 0 to δ uniformly as the pulse moves uniformly from emitter to receiver, so we have ωt = λδ. Therefore, inserting the x and y coordinates into the transformation equations, we get

Expanding these expressions and simplifying, we get the parametric equations for the path of light in terms of the rotating coordinates in which the disk is stationary

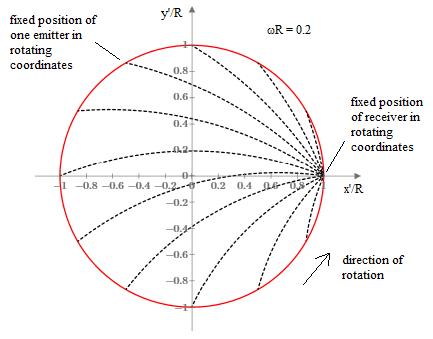
To illustrate, consider a disk of radius R and angular speed ω such that ωR = 0.2.  (This is the speed of a point on the perimeter of the disk.) In terms of the rotating coordinates we place the receiver at [R,0], and we place fixed emitters every π/6 radians around the perimeter. The paths of light from each emitter to the receiver are shown in the figure below.

As expected, the rays have an outward curve (relative to the linear path) for the counter-rotating direction, and an inward curve for the co-rotating direction.

It should be noted that, in applying the parametric formulas to generate these paths for a given value of ωR and various values of θ, the value of δ is a function of θ, since the amount of rotation during the time of flight depends on the position of the emitter relative to the receiver. Therefore, for each emitter position θ we must solve equation (1) for the corresponding value of δ.

Incidentally, people sometimes confuse the actual paths of light from a moving emitter to a moving receiver (in vacuum, flat space-time), which are necessarily linear in terms of any inertial coordinates (as required by conservation of momentum), with the locus of simultaneous positions of all the photons in flight between emitter and receiver at any given instant of coordinate time. The latter is not actually the path of any single inertial entity through time (such as a photon or pulse of light), but rather an instantaneous arrangement of a set of entities, each of which is following a linear path (in terms of inertial coordinates) from the emitter at various points of emission to the receiver at the corresponding points of reception. Naturally such an arrangement may be non-linear, depending on the motions of the emitter and receiver.

For the case of an emitter and receiver attached to the rim of a rotating unit disk, we can easily write down the parametric equations for the locus of photons in flight at a given instant in terms of an inertial coordinate system. Let θ denote the angular separation between emitter and receiver at any instant, and let δ denote the angular travel of the disk during the time required for a photon to propagate from emitter to receiver. If the first photon was emitted at [1,0], it has followed the linear path from [cos(0),sin(0)] to [cos(θ+δ),sin(θ+δ)] and is just arriving at the latter point. Likewise the last photon is just departing from the emitter on the linear path from [cos(δ),sin(δ)] to [cos(θ+2δ),sin(θ+2δ)]. As the parameter λ ranges from 0 to 1, the position of the corresponding photon at the instant when the first photon reaches the receiver is therefore

Separating the individual coordinates, this gives the explicit parametric equations

With θ = π/2 and δ = π/12, a plot of the representative locus of photons in flight is shown below.

It should be emphasized that this is not the path of any photon or pulse of light, it is simply the arrangement of photons in flight at a given instant. The actual paths of light (in vacuum, flat space-time) are always linear in terms of inertial coordinates, and of course such paths are non-linear when expressed in terms of rotating coordinates, as described previously.

Return to MathPages Main Menu