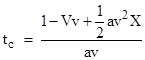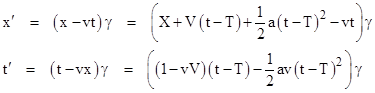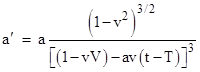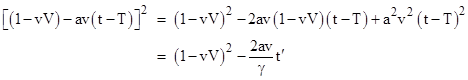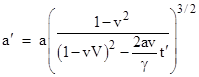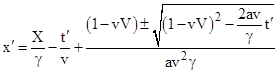Intersecting Loci With Constant Separation

You shall hear I am run away: know it

before the report come. If there be breadth enough

in the world, I will hold a long distance. My duty

to you.

                                                Shakespeare

Consider two inertial coordinate systems S and S′ with the spatially aligned coordinates x,t and x′,t′ respectively.  The spatial origin of S′ is moving in the x direction with speed v in terms of S. Suppose two particles are both moving with constant speed V along the x axis in terms of S, and then at time t′ = 0 of S′ they both begin to undergo acceleration that has a constant value “a” in terms of S.

It is sometimes suggested that this scenario leads to a paradox, because in terms of S′ the spatial distance between the particles remains constant, so the particles never collide, whereas in terms of S the spatial distance between the particles decreases, because they begin to undergo constant acceleration at different times. One might think that, when described in terms of S, the particles must eventually collide, contradicting the fact that they don’t collide when described in terms of S′.

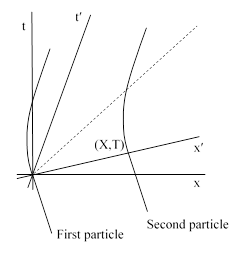
The resolution of the paradox is that the particles do not collide, because with any constant acceleration “a” in S at least one of the particles will reach the speed of light while the particles are still separated. To prove this, note that we can position our coordinates so that in S the acceleration of one particle begins at the origin x=0, t=0, and the acceleration of the other particle begins at x=X, t=T, as shown in the plot below.

Throughout our discussion we use units such that c = 1. Thus x and t both have units of (say) seconds, velocities are dimensionless, accelerations have units of 1/seconds, and so on. The equations of motion of the two particles while they are undergoing constant acceleration are

Since the accelerations begin simultaneously in S′, we have T = vX. Making this substitution and setting the x values of these two trajectories equal, we can solve for the time of collision (assuming the acceleration in S remains constant).  This gives

Differentiating the expression for x of the first particle gives the velocity as a function of t.  Setting t to the time of collision, we find that the velocity of the first particle in terms of S at the time of collision would be

Note that this is independent of V. For any v less than 1 the quantity 1/v exceeds 1, and if avX is positive the second term just increases the sum, so the velocity at the velocity at the time of collision would exceed 1 (the speed of light). One might think we could evade this by setting “a” to a negative value that brings the sum down below 1. However, by the same method we can show that the velocity of the second particle at the time of collision is

Thus, regardless of the sign of avX (which equals aT), at least one of the particles would need to exceed the speed of light at the time of collision.

This disposes of the alleged paradox of the two particles, but one might still wonder about a slightly modified question involving arbitrary loci in spacetime, not necessarily always timelike. In this case we clearly have a point of intersection between the two loci when expressed in terms of S, so there must be a point of intersection between the loci when expressed in terms of S′, and yet the loci are separated by a constant x′ interval in terms of S′. How can the loci intersect if they are separated by a constant distance?

Before answering this question, let us first give the explicit expression for the acceleration of the loci in terms of S′. For any locus with initial velocity V in terms of S and subject to constant acceleration “a” in terms of S beginning at the time t′=0 in terms of S′, we have

with T = vX. Therefore, the transformed coordinates are

where γ = (1–v²)^–1/2. We can derive the acceleration in terms of S′ most economically by making use of the expression

Evaluating the derivatives and simplifying, we get

Notice that the square of the quantity in square brackets is

Therefore we have

This confirms that a′(t′) is the same for every particle or locus that begins its acceleration at t′ = 0 in S′ and that has the initial velocity V and constant acceleration “a” in S. Consequently, the two loci are separated by a constant x′ difference at any given t′. Nevertheless, the two loci intersect, as we know they must, since they intersect in terms of S.

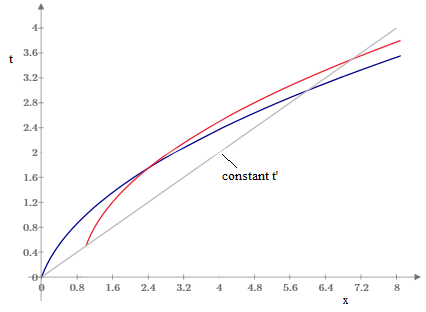
To understand this in detail, consider a specific example, with v = V = 0.5, a = 1, and X = 1. Since v and V are equal in this case, the particles are initially at rest in S′. We can first look at the loci of the two particles plotted in terms of S as shown below. Notice that the loci are single-valued for any given t, and the extend to infinite t.

From this plot the resolution of the puzzle is already obvious. The distance between the two loci is indeed constant along any line of constant t′, and yet the loci intersect (albeit after the worldlines have exceeded the speed of light). To see this even more clearly, we can eliminate t from the expressions for x′ and t′ to give an explicit expression for x′ as a function of t′

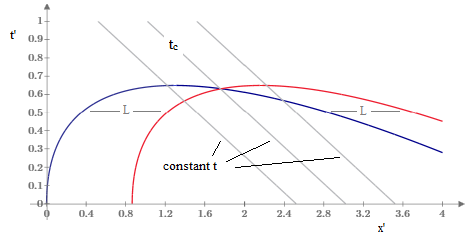
With this we can plot the two loci on a spacetime diagram for x′,t′, as shown below.

This shows that the loci are double-valued for any given t′, and they both have maxima at about t′ = 0.65. We’ve shown lines of constant t, including the time of intersection, t_c. Each locus has two branches, meeting at the maximum point. The intersection occurs between one branch of the first locus and the other branch of the second locus, but corresponding branches are always separated by a constant distance along lines of constant t′.

Incidentally, if we don’t require the accelerations to start simultaneously in some frame of reference but instead allow the accelerations to begin at (0,0) and (X,T) for arbitrary X and T, we can construct interesting puzzles even in a Newtonian context. In this context the time of collision between particles is (X – VT + (a/2)T²)/(aT), and the speeds of the two particles at the time of collision are X/T + (a/2)T and X/T – (a/2)T. Thus the average of the speeds of the two particles at the time of collision is simply X/T, independent of both the initial speed V and the acceleration a. For example, suppose two trains on the same track are initially moving in the same direction at the same constant speed, and then at some instant the trailing train begins to accelerate at a constant rate, and then at some later time the leading train begins to accelerate at the same rate. If the distance between the points where the trains begin to accelerate is X = 100 miles, and the time between when they begin to accelerate is T = 0.5 hours, the average of the train speeds at the moment when they collide is 200 miles per hour.

Return to MathPages Main Menu