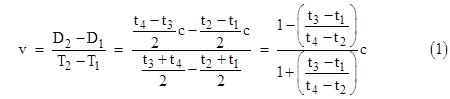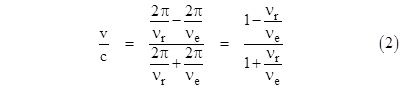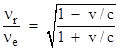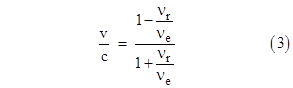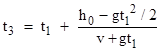LIDAR Speed Guns

The radio is playing some forgotten song…

                                           Golden Earing

There’s a widespread misconception (at least in popular expositions) that LIDAR speed guns do not use the Doppler effect to measure speed. For example, one web site, while acknowleding that radar guns use the Doppler effect, claims that LIDAR speed guns “use a more direct method that relies on the reflection time of light rather than Doppler shift”. That claim is mistaken, based on a fundamental misunderstanding. To understand why, first recall that both radar and LIDAR can be used to measure the distance to a target by evaluating the difference between the time t₁ of the emission of a pulse and the time t₂ of the reception of the reflected pulse, and then computing the distance D₁ = (t₂ – t₁)c/2. However, this does not tell us the speed of the target.

To determine the speed (i.e., the rate of change of the distance), the device must emit another pulse (or wavecrest) at later time t₃, and receive the reflected pulse at time t₄, from which we could compute the distance D₂ = (t₄ – t₃)c/2. But knowing D₁ and D₂ still doesn’t tell us the speed, we also need to know the time interval between those distance measurements. Thus if we know (say) the time interval t₃ – t₁ between the consecutive pulses or wavecrests, we can then compute the rate of change of the distance.

Now, in the frame of the LIDAR or radar gun, D₁ was the distance of the target at the time of reflection of the first pulse (or wavecrest), which was T₁ = (t₁ + t₂)/2, half-way between emission and reception. Likewise D₂ was the distance of the target at time T₂ = (t₃ + t₄)/2. Therefore, the speed v of the target based on these two measurements is

The right hand expression shows that the speed depends only on the ratio of the two intervals t₃–t₁ and t₄–t₂, which are, respectively, the interval between consecutive emissions and the interval between consecutive receptions. It does not depend on the round trip time for a pulse, and hence does not depend on the distance at all. This is equally true for radar wavecrests and LIDAR pulses. Of course, we can make devices (either radar or LIDAR) that measure distances by measuring the round trip time, e.g., t₂–t₁, but that quantity (as well as t₄ – t₃) is irrelevant to the determination of the speed, which depends only on the ratio of the quantities t₃ – t₁ and t₄ – t₂. It’s true that the quantities t₄ – t₃ and t₂ – t₁ appear in the numerator of the third expression in (1), but the denominator involves the corresponding sums, which cannot be inferred from those differences. The information that is both necessary and sufficient to infer the rate of change of the distance is the ratio of (a) the time between consecutive emissions and (b) the time between consecutive receptions. Again, this applies to both radar and LIDAR (not to mention sonar and any other similar kind of device), and it doesn’t matter if the timing is for consecutive wavecrests or consecutive pulses.

To see in detail how this relates to the Doppler effect, note that the difference t₃ – t₁ is the time between consecutive emissions (of consecutive wavecrests in a radar speed gun and of consecutive pulses in a LIDAR speed gun), so the emission frequency is ν_e = 2π /(t₃–t₁). Likewise the difference t₄ – t₂ is the time between consecutive receptions, so the reception frequency is ν_r = 2π /(t₄–t₂). Thus we can write equation (1) as

Recall that the familiar relativistic Doppler formula for a one-way signal is

and for a round-trip signal the Doppler frequency shift is the square of the right-hand expression, so we have

Solving this for v/c gives

which is identical to the formula (2), which is simply a re-writing of formula (1), used in a LIDAR speed gun to determine the speed. Needless to say, the round-trip Doppler shift formula given by equation (3) is also the equation used in radar speed guns. Thus LIDAR and radar both use the Doppler effect to determine the speed of the target, and the result depends only on the ratio of the reception frequency to the emission frequency, not on the distance to the target. Of course, we may build a device (either LIDAR or radar) that also determines distances, in which case the total round-trip time for the reflected signals must be measured, but this is distinct from the determination of the rate of change of the distance.

The mistaken idea that radar uses the Doppler effect but LIDAR does not highlights a more fundamental misconception. Note that the web page cited above said radar sends out a radio pulse, waits for the reflection, and then measures the Doppler shift. Since the Doppler effect involves frequency, the web page is tacitly assuming that an individual “pulse” has some identifiable frequency. Classically this would imply that the “pulse” actually consists of a short burst with a certain frequency, i.e., several wave crests of an electromagnetic wave. The period (i.e., time interval between consecutive wave crests) of the transmitted wave is then compared with the period of the received wave, exactly as in the LIDAR gun. Expressed in terms of frequency, the radar gun uses the Doppler equation (3), just as does the LIDAR gun. The only difference is that a radar gun deals with the frequency of the carrier wave, whereas LIDAR deals with the frequency of a signal wave, as depicted below.

The radar gun in effect measures the period of the waves that comprise a burst, whereas the LIDAR gun measures the period between bursts. But in either case the ratio of the transmitted and received periods is obviously the same, given by the (squared) Doppler factor. Naturally there are different methods of measuring the period or frequency or wavelength of a signal. We could use a tuning analog detector that is excited by a range of frequencies, or a differential circuit that directly responds to the difference between emitted and received frequencies. Alternatively we could measure the time intervals between consecutive wave crests or pulses. Radar guns and LIDAR guns ordinarily use different methods for measuring the frequencies, but for purposes of determining speeds they both rely on determining the ratio of transmitted to received frequencies (or periods) using the standard Doppler formula.

Some of the misunderstanding of this subject is due to the fact that the Doppler effect is almost always defined – even in reputable sources – explicitly as an attribute of “waves”. The word “wave” is somewhat ambiguous, but clearly the Doppler effect applies to any sequence of propagating entities, whether they are wavecrests or pulses or bullets or anything else. The effect is simply a consequence of the tautological fact that at a given speed an entity takes less time to traverse less distance. As such, it provides a clear basis for evaluating the rate of change of distances. Indeed, aside from parallax, it’s difficult to imagine any way of inferring the speed of an object from reflected signals other than by the Doppler effect, i.e., by exploiting the fact that the distance is changing so the rate of reflected pulses is different than the rate of transmitted pulses, because the distance each pulse must travel is changing. So how could anyone even entertain for a moment the possibility that LIDAR guns do not rely on the Doppler effect?

One underlying misconception seems to be the idea that an electromagnetic wave possesses and exhibits a frequency that is somehow different from the frequency of arrival of successive wave crests. The online reference cited earlier described radar in terms of the frequency of a radio pulse, but it would be more accurately described as a burst comprised of a small number of cycles with a characteristic period, as depicted in the figure above. The word pulse tends to suggest a single entity with no internal structure (like a Dirac delta function impulse), and it seems to be vaguely associated in the minds of some people with the concept of a photon in quantum theory. Indeed the well-known expression E = hν gives the relationship between the frequency of light and the energy of the photons comprising that light. Since an individual photon has a certain energy, this leads some people to the mistaken idea that an individual photon has a frequency.  It is true that quantum interference effects are exhibited by individual photons (such as in a two-slit experiment with extremely low intensity source), but this does not imply that an individual photon has a frequency in the temporal sense, and the interference effects can reveal the frequency only by the distribution of many photons.

Needless to say, radar guns do not examine individual photons or quantum interference effects for a sequence of photons. It would be possible in principle to pass a large number of individual photons through a two-slit apparatus until the interference pattern became evident, and then deduce the frequency of the light from that pattern, but this still would not enable us to derive a frequency from timing of a single photon. Alternatively we could measure the energy of a photon and infer the associated frequency from the relation E = hν, but we would find that the ratio of transmitted and received energies is the same as the ratio of frequencies of a classical wave.

In some ways it is more useful to regard a photon as a discrete transfer of energy along a null interval. The phase of the quantum wave function of a pulse of light or photon does not advance at all during transit. (In general, the advance of the quantum wave function of any system passing between two events is proportional to the proper time interval along the path, which is zero for massless energy.) Rather than saying a photon has a frequency it is better to say the source has a frequency. The source (atom) is in null contact with the receiving system (atom), in general via multiple paths through spacetime, and the amplitude for a transfer to occur from any given emitter’s worldline to a given reception point is the superposition of the amplitudes for all possible piece-wise null paths. Thus the frequency over a range of events at the source is imposed on the receiving event, and this accounts for the wave-like interference effects.

The misconception about intrinsic temporal frequencies of individual photons arises in other contexts as well. For example, in discussions of gravitational redshift we sometimes see claims that the difference in frequency is not due to time dilation but rather due to “something happening” to the signals (photons) in transit from one gravitational potential to another. The classical image is of a ballistic particle losing speed as it rises in a gravitational field, and some people vaguely associate this with a drop in frequency, but of course in a stationary situation each particle would slow by the same amount, so this would not affect the frequency of arrival. Likewise the wave crests of a light wave would take the same time to climb, so we cannot attribute the difference in arrival frequency to something that happens to the pulses (or bullets, or wave crests, or whatever). The difference can only be due to time dilation between the locations of different gravitational potential.

To illustrate, consider the following purported explanation of how gravitational redshift follows from the equivalence principle (Michael Fowler):

Suppose a flash of light leaves the ceiling [of an elevator] at the instant the elevator is released into free fall.  If the elevator has height h, it takes time h/c to reach the floor. This means the floor is moving downwards at speed gh/c when the light hits… By the Equivalence Principle, conditions are identical to those in an inertial frame with no fields present, [so] there is nothing to change the frequency of the light [when it hits the elevator floor].  This implies, however, that to an outside observer, stationary in the earth's gravitational field, the frequency of the light will change.  This is because he will agree with the elevator observer on what was the initial frequency f of the light as it left the laser in the ceiling (the elevator was at rest relative to the earth at that moment) so if the elevator operator maintains the light had the same frequency f as it hit the elevator floor, which is moving at gh/c relative to the earth at that instant, the earth observer will say the light has frequency f(1 + v/c) = f(1+gh/c²), using the Doppler formula for very low speeds. We conclude from this that light shining downwards in a gravitational field is shifted to a higher frequency.

The reasoning is invalid, due to the misconception in the first sentence, referring to a “flash of light” emitted at an “instant”, followed by an attempt to reason about the frequency of this instantaneous flash. The reasoning also fails to distinguish between a Newtonian and Einsteinian context. To unravel this, recall first that genuine gravitational frequency shifts correspond to gravitational time dilation between points of different gravitational potential, so they apply to all processes, not just to the frequencies of electromagnetic signals. In particular, we can consider shooting bullets from a gun at a certain rate, and then note that the rate of arrival of those bullets at some other gravitational potential exhibits the same characteristic frequency shift factor that applies to the frequency of light.

Now, the equivalence principle is satisfied by Newtonian mechanics, and yet there is no gravitational redshift in Newtonian mechanics, neither for a stationary car on the Earth’s surface nor for an accelerating car out in space (as we’ve discussed elsewhere). But there is also no frequency shift for a car in freefall. So how does Fowler’s reasoning fail in the Newtonian context? Let t₀ and t₁ denote the times when bullets are fired downward from the top of an elevator car that is released from rest at time t₀, and let v denote the speed of the bullets relative to the car, assumed to be great enough (for the given acceleration) so that the speed doesn’t change appreciably during the time required to traverse the car. Also, let t₂ and t₃ denote the arrival times of the bullets at the initial position of the floor of the car (where the stationary observer is located). The height of the ceiling is h = h₀ – gt²/2 and the speed is dh/dt = –gt. We have t₂ = h₀/v and

Hence we have

In the limit as t₁ approaches zero (i.e., as the time between the firing of the two bullets goes to zero, so we approach a single “pulse”), the ratio of times approaches

Taking v = c, and noting that the frequency is the inverse of the period, this gives to the first order the frequency shift factor 1 + gh/c². But this does not imply gravitational frequency shift, because this entire effect is due to the fact that the second bullet is fired from a slightly lower position and with a slightly greater downward speed, due to the movement and acceleration of the car during the interval between firing, even in the limit as the interval approaches zero. If, on the other hand, we fired two bullets from the top of a stationary car, the same analysis would show that the interval between their arrival times would be the same as between their firing times. In the Newtonian context, there is no frequency shift for a stationary car in a gravitational field, just as there is none for an accelerating car in space. Thus Newtonian mechanics satisfies the equivalence principle, but there is no gravitational frequency shift.

As we’ve discussed elsewhere, the actual frequency shift for an accelerating car in space is due to the non-Newtonian velocity addition formula of special relativity, and the associated time dilation, from which the equivalence principle implies that there must be gravitational time dilation with the associated frequency shifts. In other words, gravitational redshift doesn’t follow from the equivalence principle alone, it follows from the combination of the equivalence principle and special relativity. This is obscured by the confusion that arises from trying to reason about the frequency of a single instantaneous pulse.

Return to MathPages Main Menu