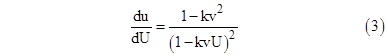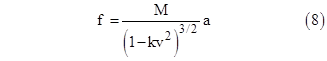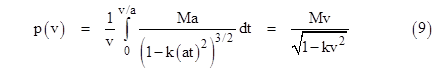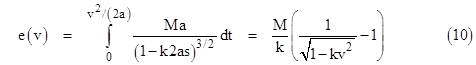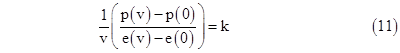Energy Conservation and Lorentz Invariance

One way of expressing Lorentz invariance is in terms of the relationship between relatively moving systems of space and time coordinates, in each of which the equations of mechanics take their simple homogeneous and isotropic form, or, equivalently, “in which the equations of Newtonian mechanics hold good” in the low speed limit. This class of coordinate systems is usually referred to as inertial coordinate systems (not to be confused with the larger class consisting of unaccelerated systems, i.e., systems in which only Newton’s first law is stipulated to hold good).

From the definition, nothing guarantees that even one inertial coordinate system actually exists, because it’s conceivable that mechanical phenomena might not be homogeneous and isotropic in terms of any coherent system of coordinates. However, during the 16^th and 17^th centuries, with the work of Galileo, Newton, and others, it became clear that not only does there exist one system of inertial coordinates, there exist infinitely many. This led to the formulation of the principle of (mechanical) relativity, according to which, for any object in any state of motion, there exists an inertial coordinate system in which the object is instantaneously at rest. Galileo implicitly extended this to all phenomena (not just mechanics), saying that, inside a cabin moving at constant speed in a straight line, it is as if the motion does not exist. In an early draft of the Principia, Newton placed the relativity principle among the “five laws of motions”, but later trimmed them down to three, and derived the relativity of mechanics in his famous Corollary V. This was fairly immediate, noting that his three fundamental laws depend only on acceleration, not on position or velocity.

When electromagnetic phenomena came under study during the 18^th and 19^th centuries, the natural expectation was that they too would satisfy the relativity principle, although there was some uncertainty, because electromagnetic waves (identified with light) evidently do not have mass, so it was unclear if the relativity of mechanics (of massive inertial bodies) would apply.

However, during the same years, the concept of energy came to the forefront of physics. Newton had emphasized momentum as the quantification of motion, but others (notably Leibniz) had highlighted the significance of kinetic energy. Subsequently the equivalence of various other forms of energy, including thermal, potential, and electromagnetic, was established. Ultimately this led to the formulation of the principle of energy conservation, which signifies that energy is a real palpable thing that can neither be created nor destroyed, but that can only move contiguously from place to place, and hence must be subject to dynamical laws.

According to Newtonian physics, the center of mass of an isolated system must move at constant speed in a straight line, but the center of energy did not. This appears as a glaring anomaly in Newtonian physics as soon as the conservation of energy is established. The only remedy is for inertia to be strictly proportional to energy, with a strict identification of mass with an equivalent amount of energy. Thus energy has inertia, and this implies that the dynamical equations of any kind of energy (mechanical, electromagnetic, or any other) must take their simple homogeneous and isotropic form in terms of the very same class of coordinate systems, i.e., the inertial coordinate systems.

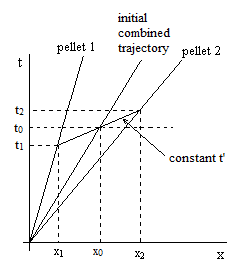
But the proportionality of inertia and energy also tells us more. Not only does it ensure that the principle of relativity extends to all physical phenomena, it singles out the Lorentzian (as distinct from Galilean) form of relativity. It implies that the time coordinates of relatively moving systems of inertial coordinates are skewed, because two identical pellets moving together at speed v and then pushing against each other along the axis of motion so they acquire speeds ±u in terms of their initial frame will not have equal inertial masses in the stationary frame, because of their different kinetic energies – the particle in the forward direction will be going faster than the particle in the rearward direction. (This assumes momentum is conserved.) Hence their speeds will not be v±u in the stationary frame, and yet they must travel equal distances in equal times according to their initial frame, so the time coordinate of that frame must be skewed as depicted below.

To show this quantitatively, first recall that the definition of inertial coordinate systems (if they exist), along with reciprocity and isotropy, implies that any two relatively moving such systems are related by a transformation of the form

for some constant k with units of inverse square speed, and this corresponds to the formula for the composition of speeds

Consider a system of inertial coordinates s, and another such system S with aligned axes moving in the positive x direction with speed v in terms of s, and suppose a particle is moving in the positive x direction at speed U in terms of S. Differentiating the above expression with respect to U gives

At a condition when the particle is momentarily at rest in S (meaning U=0) we have

Also, inverting the coordinate transformation in differential form, we have

so at the condition when U = 0 (and hence dX = 0) we have

Combining this with equation (4), we get the relation between the accelerations of the particle in terms of the two coordinate systems

The quantity  a = du/dt  is the acceleration of the particle with respect to the s coordinates, whereas A = dU/dT  is the acceleration of the particle with respect to the S coordinates (relative to which it is momentarily at rest). Now, by symmetry, a force F exerted along the axis of motion between a particle at rest in s on an identical particle at rest in S must be of equal and opposite magnitude with respect to both frames of reference. Also, by definition, a force of magnitude f applied to a particle of “rest mass” M will result in an acceleration A = F/M with respect to the reference frame in which the particle is momentarily at rest. Therefore, using the preceding relation between the accelerations with respect to the s and S coordinates, we have

The momentum p of a particle of speed v is the integral of f dt over an interval in which the particle is accelerated from rest to the speed v. Likewise the (kinetic) energy e of the particle is the integral of f ds over that same interval. This energy equals the work done on the particle, and the process is reversible, i.e., after we accelerate the particle by doing work on it, the particle can then do an equal amount of work on its surroundings and thereby be decelerated back to its initial state. Hence p and e are state variables for a given speed v, independent of how the particle arrived at the speed v. Thus we can consider the case of constant a, and integrate f dt over the time interval from t = 0 to t = v/a. Likewise we integrate f ds from s = 0 to s = v²/(2a). This gives the results

The inertial rest mass of the particle is simply p(0)/v = M, and the increase of inertial mass due to the speed v is [p(v)–p(0)]/v. The ratio of this to the increase of energy is

This shows that k (an inverse square speed) is the constant or proportionality between energy and inertia. In Newtonian physics it was assumed that energy (to the extent that it was even recognized as a definite entity) had no inertia, meaning k = 0, and so the relationship between inertial coordinate systems would be the Galilean transformation. The realization that inertia is proportional to energy implies a non-zero value of k. It also implies that energy is proportional to inertia, and so the energy of the particle at rest is M/k, and the total energy E of the particle is

From this it follows that

Hence any massless energy (M=0) with non-zero momentum p must propagate at the speed v = 1/√k. This is also the asymptotic speed to which a massive particle approaches as the energy approaches infinity, such as if subjected to a constant force. Letting “c” denote the quantity 1/√k, we complete the specification of the Lorentz transformation, and we also have

Incidentally, we alluded above to the possibility of confusion over the meaning of “inertial coordinate system”. At the grade school level an inertial coordinate system is often defined as a system of coordinates in which Newton’s first law holds good, which is to say, an object not acted upon by any external forces moves at uniform speed in a straight line, but this simplistic definition is both ambiguous and problematic – for several reasons.

First, it doesn’t specify whether it is referring to a system of space coordinates, or a system of space and time coordinates. In the Newtonian context there was just a single absolute time, so the time parameter was typically not even regarded as a coordinate. In that context (which persists to the present day in introductory physics courses) a “coordinate system” referred to just space coordinates. But the assertion of Newton’s first law pertains to motion, which involves time, so it really needs to refer to a system of space and time coordinates.

Second, the meaning of the words “uniform speed in a straight line” is ambiguous, because it doesn’t give any independent criteria for judging the uniformity of speed or the straightness of lines. One might try to remedy this by saying that, in terms of coordinates x,y,z,t the position coordinates x,y,z are each linear functions of the time coordinate t. This is clear, but it isn’t generally true. Newton’s first law, expressed in this unambiguous form, holds good only if x,y,z,t is a coordinate system in which Newton’s first law is holds good (e.g., not an accelerated system). There is some circularity in defining inertial coordinates using Newton’s law, whose definition refers to inertial coordinate systems.

Third, the reference to external forces in Newton’s first law is ambiguous, because we have no a priori way of knowing whether an external forces is being applied other than by checking to see if the object is deviating from uniform speed in a straight line. This is why critics have often pointed out (only half in jest) that Newton’s first law amounts to saying that objects always move at uniform speed in a straight line except when they don’t.

Fourth, specifying a system of coordinates in which Newton’s first law holds good is not sufficient to ensure that all of Newton’s laws hold good, even in the low speed limit. For example, beginning from a coordinate system in which mechanical inertia is homogeneous and isotropic and Newton’s laws hold good in the low speed limit, we can obviously skew (tilt) the time coordinate, and Newton’s first law will still be satisfied, but the law of equal action and reaction will not.

Fifth, referring to “laws” holding good is problematic, because the laws can be conceived as generic relations that can be expressed in terms of arbitrary coordinates by suitably conditioned equations. What we really mean is that the Newtonian equations of mechanics, in their simplest homogeneous and isotropic form, with no “extra” terms, hold good. This limits us to coordinates that are not only unaccelerated and rectilinear, but that also have a time foliation conforming to the isotropy of inertia.

Sixth, even if we refer to all of Newton’s equations, rather than just the first, we must deal with the fact that Newton’s equations are not actually valid in terms of any coordinates, so we need to place a restriction such as “to the first approximation” (as in the footnote in Einstein’s paper) or “in the low speed limit”. Alternatively we can avoid referring to Newton’s equations at all, and simply stipulate that the equations of physics (whatever they may be) take their simple homogeneous and isotropic form. We must also specify reciprocity.

To avoid all these problems and ambiguities, we proceed as above, by first defining “inertial coordinate system” as a system of space and time coordinates in which the equations of Newtonian mechanics in their isotropic and homogeneous form hold good in the low speed limit, and then asserting (principle of relativity) that for any material particle in any state of motion there exists an inertial coordinate system in which the particle is instantaneously at rest. We then further assert (along with reciprocity, memorylessness, etc.) that energy E has inertia E/c² and vice versa.

Return to MathPages Main Menu