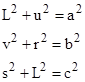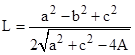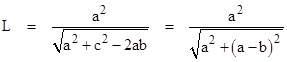|
Triangle in a Square |
|
|
|
So hallow'd and so gracious is the time. |
|
Shakespeare |
|
|
|
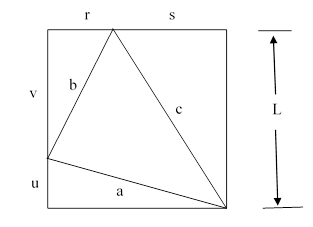
Consider an arbitrary triangle inscribed in a square as shown below. |
|
|
|
|
|
|
|
Given the edge lengths a,b,c of the triangle, we seek the square’s edge length L. By Pythagoras’ theorem we have the conditions |
|
|
|
|
|
|
|
along with the relations u + v = r + s = L. Eliminating u,v,r,s from these expressions, we get the quadratic in L2 shown below: |
|
|
|
|
|
|
|
where A is the area of the inscribed triangle, given by Heron’s formula |
|
|
|
|
|
|
|
Solving the equation for L gives the result |
|
|
|
|
|
|
|
Incidentally, in the special case when a2 + b2 = c2, so that the inscribed triangle is a right triangle, this reduces to |
|
|
|
|
|
For example, with a=4, b=3, and c=5 the edge length of the square is L = 16/√17. Naturally the result in this specialized case can be derived very simply from similar triangles, given that the inscribed triangle is a right triangle, but the general result for arbitrary triangles is much more interesting. This illustrates a common feature of puzzles and artificial problems, namely, that they consist of a general problem whose solution would be somewhat laborious, but the specified parameters are tailored (fine-tuned) to yield a degenerate case with a much easier solution. Other examples of this are the problem of the Swiss triangle and the catenary job interview question. In each case the underlying general problem leads to more interesting results than the specialized question. |
|
|