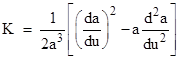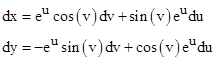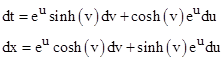Conformal Coordinates

The metric line element on a flat plane in terms of Cartesian coordinates x,y is

Thus the metric tensor g_μν has the components (by row) 1, 0, 0, 1, and of course the Gaussian curvature K of this surface is 0, as can be trivially verified using the formula in the chapter on curvature in Reflections on Relativity, because every term involves a first or second derivative of the (in this case constant) metric components.

Now consider a two-dimensional surface on which we can define a coordinate system u,v such that

where a(u) is some specified function. This is called a conformal metric, because it has a flat “factor”. The components of the metric tensor (by rows) are a(u), 0, 0, a(u), and we can once again use the formula for the Gaussian curvature to find that

In general this is not zero, but if we set a(u) = e^2u we have K=0. This implies that we can construct a system of coordinates on a flat plane such that the metric line element is (2). Indeed if we define the coordinates u and v implicitly from the Cartesian coordinates x,y by the relations

then we have the total differentials

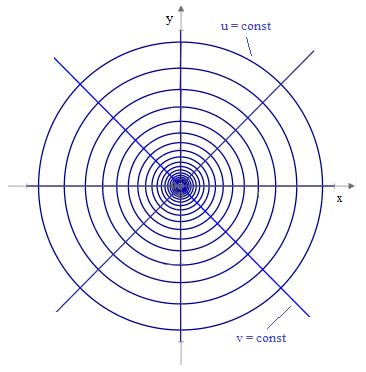
Inserting these into (1) gives (2) with a(u) = e^2u, as was to be shown. The u,v coordinates on the plane are essentially just polar coordinates with an exponentially increasing radial coordinate, as depicted in the figure below.

The analogous relations apply to 1+1 dimensional space-time, which in terms of standard inertia-based coordinates t,x, has the pseudo-metric line element

In this case we define the coordinates u and v implicitly from the Cartesian coordinates x,y using hyperbolic trigonometric functions by the relations

then we have the total differentials

Inserting these into (3) gives

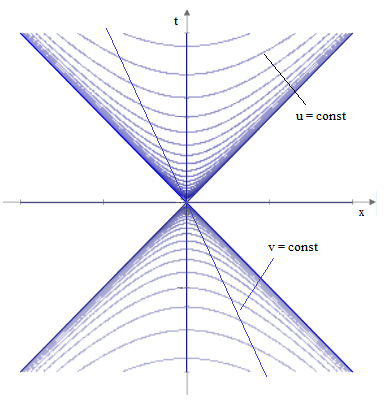
where a(u) = e^2u, as was to be shown. This clarifies why such metrics are called conformal, because null intervals satisfy (du)² – (dv)² = 0, so these coordinates give isotropic light speed, and hence angles physical are preserved. In this case the u,v coordinates are essentially hyperbolic coordinates, as depicted below.

Similar metrics are discussed in the article on The Infinite Wall.

Conformal re-scaling of a metric was applied by Hermann Weyl in his attempt to develop a unified theory of gravity and electromagnetism, although scaling by real factors led to un-physical predictions, such as physical characteristics of a particle being dependent on the history of the particle. However, if we use a complex factor with magnitude 1, meaning a factor of the form e^iθ where θ is the phase angle that may advance as a function of time, we can construct models that actually do represent electromagnetism and other quantum interactions.

Return to MathPages Main Menu