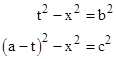Heron’s Coordinates

I do I know not what, and fear to find

Mine eye too great a flatterer for my mind.

Fate, show thy force: ourselves we do not owe;

What is decreed must be, and be this so.

                                                  Shakespeare

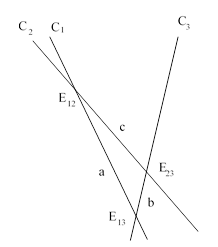
Consider three ideal clocks, C₁, C₂, C₃, in different states of inertial motion along a single line, and let E_ij (or, equivalently, E_ji) denote the event at which C_i and C_j coincide. A typical example is depicted in the figure below.

We also let τ_i,jk denote the elapsed proper time on clock i between E_ij and E_ik. For convenience in the figure above we have denoted the elapsed proper times as τ_1,23 = a, τ_3,12 = b, τ_2,31 = c. Now, given the three elapsed proper times, we wish to know the coordinates of event E₂₃ in terms of the standard inertial coordinate system x,t in which C₁ is at rest and the origin is at E₁₃. We have the following relations

Solving these equations for t gives

Inserting this back into the first relation and solving for x gives

Thus, as we would expect, the “area” (1/2)ax, where a is the base and x is the perpendicular altitude of the “triangle”, equals the area of a triangle with edge lengths a,b,c as given by Heron’s formula. The same relation applies for lines on a Euclidean plane, even though the metric has a different signature.

This nicely illustrates the fact that formal notions of perpendicularity and coordinate systems defined by specified formal metrics or pseudo-metrics don’t actually single out those systems in a physical sense. The reason we regard the Euclidean metric in space, or the Minkowskian pseudo-metric in spacetime, as “correct” in a physical sense is because they match the active behavior of physical entities under changes of position, orientation, or state of motion. This is another way of expressing the form of the physical laws, since those laws govern the physical behavior of entities. We can assert that the equations of physics take their simple homogeneous and isotropic form in terms of every one of a certain class of coordinate systems, and this is essentially asserting that the equilibrium configurations of physical entities are congruent when subjected to changes in position, orientation, or state of motion.

This also shows that we can, in principle, assign standard inertial coordinates x,t in one space dimension to the intersection events of a set of identified clocks, given only the elapsed proper time intervals between their intersection events. Notice that the triples of “edge lengths” for the “triangles” with vertices given by the intersection events for three given clocks do not satisfy the triangle inequality for Minkowski spacetime. If we replace the clocks with odometers in a Euclidean plane, the edge lengths would satisfy the triangle inequality. Hence from the measures of these intervals we can infer the metric or pseudometric, but only with the assumption that the clocks are identically constructed, which ultimately signifies that they could be manufactured at mutual rest and then gently accelerated to different states of motion and allowed to reach equilibrium without suffering any persistent elastic deformation. This could be verified by gently bringing them back to mutual rest and verifying that they still tick at the same rate. Ultimately every demonstration of local Lorentz invariance must involve some active transformation of this kind, since Lorentz invariance is a property of the dynamical laws of physics, not just an artifact of formal kinematics established by decree.

Return to MathPages Main Menu