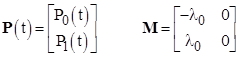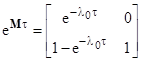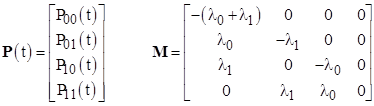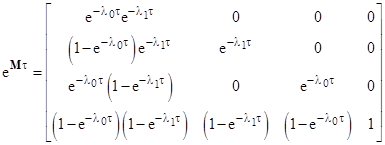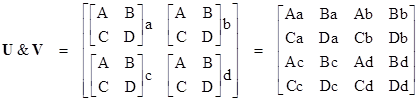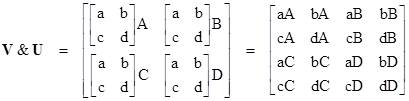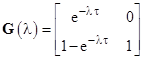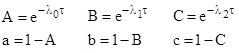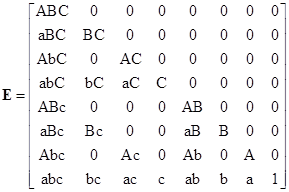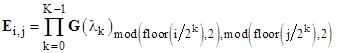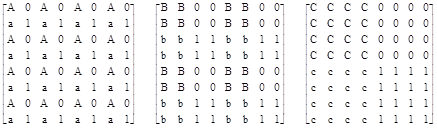|
Tiling Product of Matrices |
|
|
|
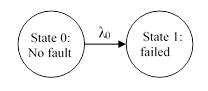
A homogeneous Markov model for failures of a single element with constant failure rate λ0 can be depicted as shown below: |
|
|
|
|
|
In terms of the state vector and transition matrix |
|
|
|
|
|
|
|
the homogeneous differential state equations for the Markov model can be written as |
|
|
|
|
|
|
|
Solving this equations, we see that, beginning at time t with any initial condition P(t), the probabilities of the states at the later time t + τ is given by |
|
|
|
|
|
|
|
Of course, the exponential factor can be computed using the power series |
|
|
|
|
|
|
|
which in this simple one-component example yields the result |
|
|
|
|
|
|
|
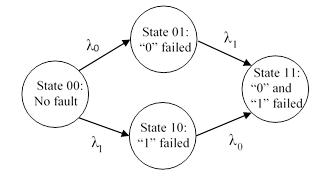
Now we go on to consider the homogeneous Markov model for failures of two independent components “0” and “1” with constant failure rates λ0 and λ1, which can be depicted as shown below. |
|
|
|
|
|
|
|
In this case we have the state vector and transition matrix |
|
|
|
|
|
|
|
The system equation and solution are again given by equations (1) and (2), with the exponential factor |
|
|
|
|
|
|
|
As can be seen, this is produced by what amounts to a tiling product of the individual component exponential matrices. Given two 2x2 matrices |
|
|
|
|
|
|
|
we can create a 4x4 matrix by weighted tiling operation as shown below. |
|
|
|
|
|
|
|
Clearly this operation is not commutative, as shown by |
|
|
|
|
|
|
|
However, if we number the four rows and the four columns in binary as 00, 01, 10, 11, these two results are equivalent is we simply swap the order of the binary bits. In this case it has the effect of swapping the middle two rows and swapping the middle two columns. |
|
|
|
This operation can be used to compute the exponential matrix in the homogeneous solution of the general Markov with K components. For any given time increment τ we first define the matrix function |
|
|
|
|
|
|
|
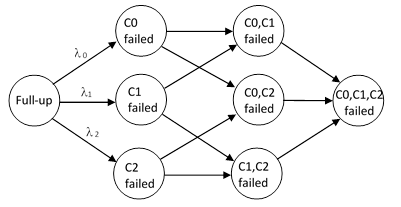
For example, consider a system with K=3 components with the constant failure rates λ0, λ1, λ2, whose Markov model is as shown below. |
|
|
|
|
|
|
|
The homogeneous solution is |
|
|
|
|
|
|
|
where |
|
|
|
|
|
|
|
This is an 8x8 matrix. Thus if we define the symbols |
|
|
|
|
|
|
|
the E matrix for this case is |
|
|
|
|
|
|
|
Carrying out the tiling operations in different orders results in essentially the same solution, merely with some permutation of the rows/columns. The order used above results in the binary numeric ordering, i.e., flipping right to left and letting 0 and 1 denote upper and lower case (healthy and failed) respectively, the ordering is 000, 001, 010, 011, 100, and so on. One way of expressing the E matrix explicitly is |
|
|
|
|
|
|
|
This consists of forming the component-wise product of the matrices |
|
|
|
|
|
|
|
This pattern is reminiscent of Fourier transforms and the Fourier series representations of functions. |
|
|