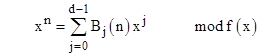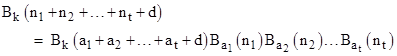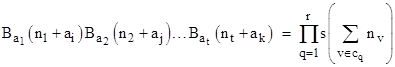|
Identities for Linear Recurring Sequences |
|
|
|
There are several methods for computing the Nth term (mod M) of a linear recurring sequence of order d in log2(N) steps, but most such methods require d2 full multiplications (mod M) per step. The algorithm described below requires only d(d+1)/2 multiplications per step. The algorithm can be described in terms of the basis sequences Bj(k), defined by |
|
|
|
|
|
|
|
where f(x) is the characteristic polynomial of the recurrence. There are several useful identities involving these sequences. In particular, we have |
|
|
|
|
|
|
|
where summation from 0 to d−1 is implied over each of the “a” indices. |
|
|
|
NOTATION: Summation from 0 to d−1 is implied over any index that appears both as a subscript and as an argument in a single term. |
|
|
|
For computing the Nth term of a linear recurrence (mod M), the most useful special case of the above identity is |
|
|
|
|
|
|
|
where r is set to either 0 or 1 according to the binary bits of N. Because of the symmetry of the right hand side, only d(d+1)/2 full multiplications are required per step. |
|
|
|
There is a nice relation between the basis sequences B and the s(n) sequences (i.e., the sums of the nth powers of the roots of f). Let {i,j,..,k} be any given permutation of the integers {1,2,..,t} with the disjoint cyclic components c1, c2,..,cr. Then we have |
|
|
|
|
|
|
|
In the most trivial case, this identity reduces to the fact that s(n) is the "trace" (or "contraction") of the basis sequences |
|
|
|
|
|
|
|
Of course, given the basis sequence elements, we can easily compute the Nth terms of any linear recurring sequence (not just s(n)) with the characteristic polynomial f(x), since every such sequence is a linear combination of the basis sequences. |
|
|