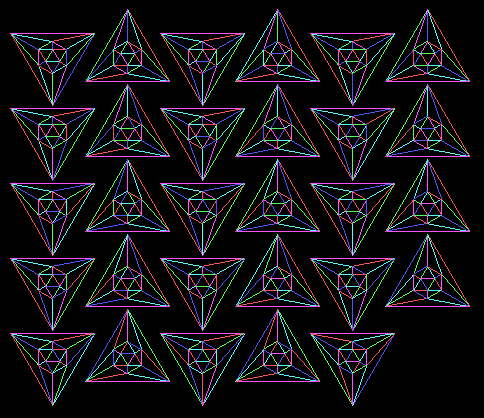Coloring The Edges of an Icosahedron
It's possible to color the edges of an icosahedron in five different
colors such that the colors of the edges meeting at each vertex are
all different. In fact, this can be done in several distinct ways.
The exact number of distinct ways depends on how we define "distinct-
ness". If we fix the orientation of the icosahedron, and assign the
five colors a,b,c,d,e to the five edges that meet at the "top" vertex,
then there are 780 distinct ways of coloring the rest of the edges
such that each color adjoins each vertex. However, if rotation of
the icosahedron is allowed, many of these colorings can be shown to
be equivalent.
One way of defining the "fundamentally distinct" colorings is to
classify them according to the numbers of distinct vertices. We
can characterize each vertex by the cycle of colors that meet at
that point, taken in clockwise order. Two vertices are said to
be equivalent if they have the same cycle of colors. We could then
say that two colorings are equivalent if they have the same numbers
of distinct vertices. On this basis there are just seven distinct
colorings, with the valencies shown below:
coloring 1 2 3 4 5 number
-------- --- --- --- --- --- ---------
#1 5 2 1 0 0 120
#2 6 3 0 0 0 120
#3 0 6 0 0 0 150
#4 8 2 0 0 0 120
#5 7 0 0 0 1 24
#6 12 0 0 0 0 216
#7 0 4 0 1 0 30
--------
total 780
For example, each of the 120 colorings in the 1st set contains 5
unique vertices, 2 sets of two equivalent vertices, and 1 set of
three equivalent vertices.
This shows that there are at least seven truely distinct colorings,
because obviously no rotations of the icosahedron or permutations of
the colors will change the vertex valencies listed above. However,
it's possible that within some (or all) of these seven categories
there are distinct colorings in the sense that, even though they
have the same valencies, they cannot be transformed into each other
by rotations or permutations.
In the preceeding discussion I split the 780 colorings into seven
classes, according to the multiplicities of their vertex equivalence
classes. (Two vertices are regarded as equivalent if they have the
same cycle of colors.) Now I've split each class into sub-classes.
Each coloring in a given sub-class has the same twelve vertex
cycles, up to permutations of the colors.
vertex
multiplicities
class 1 2 3 4 5 total sub-classes
----- - - - - - ----- --------------------------------
#1 5 2 1 0 0 120 60 60
#2 6 3 0 0 0 120 60 60
#3 0 6 0 0 0 150 30 30 30 30 15 15
#4 8 2 0 0 0 120 60 60
#5 7 0 0 0 1 24 24
#6 12 0 0 0 0 216 30 30 30 30 30 30 20 10 6
#7 0 4 0 1 0 30 30
-----
total 780
This shows that there are 23 sub-classes, so there are at least 23
truly distinct colorings that cannot be transformed into each other
by rotations of the icosahedron and permutations of the colors.
By checking every orientation of the icosahedron and every permutation
of the colors it turns out that the 23 sub-classes can be further
divided into 29 truly distinct colorings. The populations of these
29 colorings are shown below:
vertex
multiplicities breakdown of subclasses
class 1 2 3 4 5 total into distinct colorings
----- - - - - - ----- --------------------------------
#1 5 2 1 0 0 120 60 60
#2 6 3 0 0 0 120 60 60
#3 0 6 0 0 0 150 30 30 (15 15) (15 15) 15 15
#4 8 2 0 0 0 120 60 60
#5 7 0 0 0 1 24 (12 12)
#6 12 0 0 0 0 216 30 30 30 30 30 (15 15) (10 10) 10 (5 1)
#7 0 4 0 1 0 30 30
-----
total 780
Incidentally, the coloring in class #6 with just one representative
out of the total 780 is the unique pattern such that all five colors
have an identical arrangement (up to rotation), and not only does
each color adjoin each vertex only once, but each color occurs only
once on the perimeter of the pentagon surrounding each vertex. With
this pattern, the pentagon edge with a given color is always opposite
the "spoke" with that color. It follows that, since no two vertices
have the same color cycle, no two pentagon perimeters have the same
color cycle.
Here's a summary of my classes. Each coloring is represented by a
string of 30 digits in the range 1 to 5, signifying which of the five
colors is applied to the respective edge. The order of the edges in
the strings is as follows (in terms of the vertices numbered 1 - 12)
1 [1,2] 7 [2,6] 13 [4,5] 19 [6,11] 25 [7,12]
2 [1,3] 8 [2,11] 14 [4,8] 20 [6,10] 26 [8,9]
3 [1,4] 9 [2,7] 15 [4,9] 21 [11,7] 27 [8,12]
4 [1,5] 10 [3,4] 16 [5,6] 22 [11,10] 28 [9,10]
5 [1,6] 11 [3,7] 17 [5,9] 23 [11,12] 29 [9,12]
6 [2,3] 12 [3,8] 18 [5,10] 24 [7,8] 30 [10,12]
Icosahedron coloring pattern size of class
1 123453245145245135341253221143 60
2 123453245145245135342153112243 60
3 123453245145245315142351332241 60
4 123453245145245315143251223341 60
5 123453245145524123342151334512 30
6 123453245145524123342153114532 60
7 123453245145524123342511334152 15
8 123453245145524321142353114532 15
9 123453245145542312142351332541 12
10 123453245415125325142353441132 60
11 123453245415125325143254231143 12
12 123453245415215315142353442231 30
13 123453245415215315143252443321 15
14 123453245415512132342513442153 30
15 123453245415521321142353441532 30
16 123453245415521321142533441352 10
17 123453245514124325142353451132 30
18 123453245514124352142533415321 30
19 123453245514214315142353452231 10
20 123453245514214351142533425312 5
21 123453245541124325142353154132 15
22 123453245541142352143522135143 30
23 123453245541241135342153152243 30
24 123453245541241153341522335241 15
25 123453245541241351143522135243 15
26 123453425145542213311542331452 15
27 123453425541142235133452153142 15
28 123453425541142253311542335412 10
29 123454325531142253411532435412 1
As Henk Penning pointed out, the size of each of these equivalence
classes must divide 60, per the orbit/stabilizer theorem. Here's an
illustration of the 29 distinct edge-colorings of the icosahedron
with five colors such that each color touches each vertex:
Return to MathPages Main Menu