Roemer's Hypothesis

Soon after the invention of the telescope, Galileo discovered the four largest moons of Jupiter. Subsequently many astronomers made careful observations of those moons, and already by the 1660's detailed tables of their movements had been developed by Borelli (1665) and Cassini (1668). Naturally these tables were based mainly on observations taken around the time when Jupiter is nearly "in opposition", which is to say, when the Earth passes directly between Jupiter and the Sun, because this is when Jupiter appears high in the night sky. The orbital periods of Jupiter's four largest moons were found to be 1.769 days, 3.551 days, 7.155 days, and 16.689 days, and these are very constant and predictable, like a giant clockwork. Based on these figures it was possible to predict within minutes the times of eclipses and passages (i.e., the passings behind and in front of Jupiter) that would occur during the viewing opportunities in future "oppositions".

However, by the 1670's people began to make observations of Jupiter's moons from the opposite side of the Earth's orbit, i.e., when the Earth was on the opposite side of the Sun from Jupiter. Obviously it's more difficulty to make measurements at these times, because the Jovian system is nearly in conjunction with the Sun, but at dawn and dusk it is possible to observe Jupiter even when it is fairly close to conjunction. These observations, taken about 6 months away from the optimum viewing times, revealed a puzzling phenomenon. The eclipses and passages of Jupiter's moons, which could be predicted so precisely when Jupiter is in opposition, are found to be consistently late by about 17 minutes relative to their predicted times of occurrence. (The early astronomers actually measured up to 22 minutes late, but modern instruments have shown that the "lateness" is slightly less than 17 minutes.) This is not to say that the time intervals between successive eclipses is increased by 17 minutes, but that the absolute time of occurrence is 17 minutes later than was predicted six months earlier based on the observed orbital period at that time. For example, the moon Io has a period of 1.769 days, so it completes about 103 orbits in six months, and apparently it lost a total of 17 minutes during those 103 orbits, which is an average of about 9.9 seconds per orbit. All the other moons seemed to be late by the same amount when observed with Jupiter near conjunction.

Nevertheless, at the subsequent "opposition" viewing six months later, all the moons are found to be back on schedule! It's as if a clock runs slow in the mornings and fast in the afternoons, so that on average it never loses any time from day to day. While mulling over this data in 1675 on a visit to Paris, the Danish astronomer Ole Roemer thought of a beautiful explanation based on a remarkable hypothesis: "sight" is not instantaneous. Light travels at a finite speed, which implies that when we see things we are really seeing how they were at some time in the past. The further away we are from an object, the greater the time delay in our view of that object. 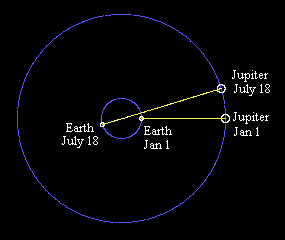Applying this hypothesis to the observations of Jupiter's moons, Roemer considered the case when Jupiter was in opposition on, say, January 1, so the light from the Jovian eclipses was traveling from the orbit of Jupiter to the orbit of the Earth, as shown in the figure below.

The intervals between successive eclipses around this time will be very uniform near the opposition point, because the eclipses themselves are uniform and the distance from Jupiter to the Earth is fairly constant during this time. However, after about six and a half months (denoted by July 18 in the figure), Jupiter is in conjunction, which means the Earth is on the opposite side of it's orbit from Jupiter. The light from the "July 18" eclipse will still cross the Earth's orbit (on the near side) at the expected time, but it must then travel an additional distance, equal to the diameter of the Earth's orbit, in order to reach the Earth. Hence we should expect it to be "late" by the amount of time required for light to travel the Earth's orbital diameter. In the late 1600's there were already some rough estimates of the mean Earth-Sun distance, so this enabled Roemer to estimate the speed of light.

Using modern estimates, the Earth's orbital diameter is about 2.98 x 10¹¹ meters, and the observed time delay in the eclipses and passages of Jupiter's moons when viewed from the Earth with Jupiter in conjunction is about 16.55 minutes = 993 seconds, so we can deduce that the speed of light is about 2.98 x 10¹¹ / 993 » 3 x 10⁸ meters/sec. (For more discussion of Roemer's actual historical estimate and its basis, see Extraordinarily Fast.)

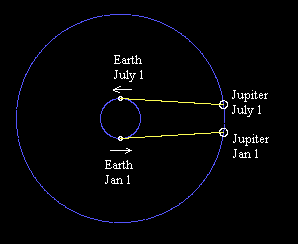
Of course, Roemer's hypothesis implies a specific time delay for each point of the orbit, so it can be corroborated by making observations throughout the year. We find that most of the discrepancy occurs during the times when the distance between Jupiter and the Earth is changing most rapidly, which is when the Earth-Sun axis is nearly perpendicular to the Jupiter-Sun axis. At one of these positions the Earth is moving almost directly toward Jupiter, and at the other it is moving almost directly away from Jupiter, as shown in the figure below.

The Earth's speed relative to Jupiter at these points is essentially just its orbital speed, which is the circumference of its orbit divided by one year. Thus we have

v  =  π(2.98 x 10¹¹) / 365  meters per day

which is equivalent to about 3 x 10⁴ meters/sec. If we choose units so that c = 1, then we have v = 0.0001. From this point of view the situation can be seen as a simple application of the Doppler effect, and the frequency of the eclipses as viewed on Earth can be related to the actual frequency (which is what we observe at conjunction and opposition) according to the formulas

The frequencies are inversely proportional to the time intervals between eclipses. These formulas imply that, for the moon Io, whose orbital period is 1.769 days = 2547.3600 minutes, the time interval between consecutive observed eclipses when the Earth is moving directly toward Jupiter (indicated as "Jan" in the above figure) is 2547.1052 minutes, and the time intervals between successive observed eclipses six months later is 2547.6147 minutes. Thus the interval between observed eclipses is 15.2 seconds shorter than nominal in the former case, and it is 15.3 seconds longer than nominal in the latter case, making a total difference of 30.5 seconds between the inter-arrival times at the two extremes, separated by six months. It would have been difficult to keep time this accurately in Roemer's day, but differences of this size are easily measured with modern clocks.

Incidentally, Maxwell once suggested that Roemer's method could be used to test for the isotropy of light speed, i.e., to test whether the speed of light is the same in all directions. Roemer's method can be regarded as a means of measuring the speed of light in the direction from Jupiter to the Earth. Jupiter has an orbital period of about 12 years, so if we use Roemer's method to evaluate the speed of light several times over a 12 year period, we will be evaluating the speed in all possible directions (in the plane of the ecliptic). The entire solar system is known to be moving with a speed of about 3.7 x 105 meters per second with respect to the cosmic microwave background radiation (i.e., the frame in which the radiation is roughly isotropic), so if we assumed a pre-relativistic model in which light propagates at a fixed speed with respect to the background radiation, and in which frames are related by Galilean transformations, this would in principle provide a means of assessing the "absolute speed" of the Earth. The magnitude of the effect is given by computing how much difference would be expected in the time for light to traverse one orbital diameter of the Earth at an effective speed of c+V and c-V, where V is the presumed absolute speed of the Earth. This gives a maximum difference of about 2.45 seconds between two measurements taken six years apart. (These two measurements each occur over a 6 month time span as explained above.) Of course, in practice it would be necessary to account for many other uncontrolled variables, such as the variations in the orbits of the Earth and Jupiter over the six year interval. These would need to be known to much better than 1 part in 400 to give adequate resolution. As far as I know, this experiment was never performed, because by the time sufficiently accurate clocks were available the issue of light's invariance with respect to inertial coordinate systems had already been established by more accurate terrestial measurements, together with an improved understanding of the meaning of inertial coordinates. Today we are more likely to establish a system of coordinates optically, and then test to verify the isotropy of mechanical inertia with respect to those coordinates.

Return to MathPages Main Menu