Twin Times

Special relativity predicts differences in the elapsed absolute proper time along two different paths between two given events. For example, consider an inertial coordinate systems (x,t) and two objects, A and B. Object A moves inertially from the point (0,0) to the point (0,1). Object B moves inertially from the point (0,0) to the point (v/2, 1/2), and from there it moves inertially to the point (0,1), as illustrated below. (We've chosen units so that c = 1.)

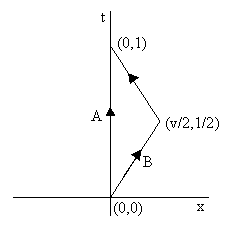
Both objects begin and end together, but their total elapsed proper times differ. The elapsed proper time for object A is simply 1, whereas the elapsed proper time for object B is .

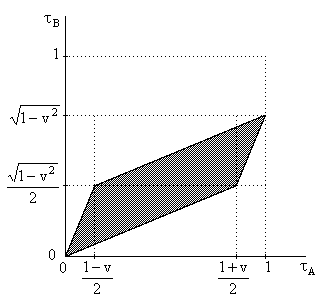
People sometimes wonder how the time of object A varies with respect to the time of object B - and vice versa - throughout the interval. However, this question implicitly assumes that the proper times of the two objects can be placed in a definite one-to-one correspondence with each other, which is not the case. In general, for any point in spacetime, the future consists of the region inside the future light cone, and the past consists of the region inside the past light cone. The region in between the future and past null cones can be called the present instant of that point. Hence if B is spatially separate from A, the present instant of any point on the path of B includes a range of distinct points on the path of A, and vice versa. Letting t_A and t_B denote the proper times of object A and B, the relationship between them is represented by the shaded trapezoidal region in the figure below.

Since the two ordinates of this plot are invariant proper times related by the intersections of light cones with the paths of the objects, this figure is invariant. In particular, this implies that the area enclosed in the "common present" region is invariant, and of course this applies to arbitrary pairs of worldlines in four-dimensional spacetime intersecting at two events. This invariant area has units of sec². In the simple case shown above, the width of the horizontal median line is v, so the enclosed area is

The maximum area occurs with v = ±1/√2, which is ±0.707... If v is either increased or decreased from this value, the enclosed area is reduced. The maximum area is 1/4.

The same quantity can be computed for any two doubly-intersecting timelike curves in spacetime, including the curved spacetime of general relativity. If we regard multiple intersections between entities as the only observable events, it's arguable that this quantity is a viable general measure of the observable relations of spacetime. It's interesting to consider the maximum possible area associated with any two doubly-intersecting plane curves. If the curve A is inertial from t = 0 to t = 1 with respect to its rest frame coordinates, then the invariant area contribution of each incremental interval along the curve B is

If curve B intersects curve A at t = 0 and t = 1, then the total invariant area of this loop is the integral

To maximize this invariant area (or actually to find the path that makes this area stationary), we can apply the calculus of variations. Letting F(t,x,v) denote the integrand in the above expression, Euler's formula gives

Evaluating these differentiations, we have

where a = d²x/dt². Multiplying through by the denominator of the right hand side, and simplifying, we arrive at

If we use x_j to denote the jth derivative of x with respect to t, this can be written as

Differentiating again with respect to time gives

Interestingly, this is a special case of the well-known "separation equation" that describes so many naturally occurring one-dimensional spatial separations (including inertial and gravitational). If we stipulate that x(0) = x(1) = 0, and that v ≤ 1, then we have the simple solution

and the invariant area between the two intersections is

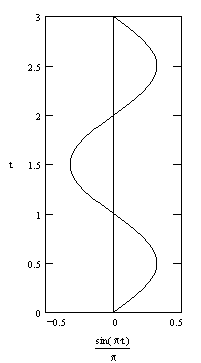
Naturally this relationship between distance and time can be continued to further intersections, so we have the interwoven world-lines shown below.

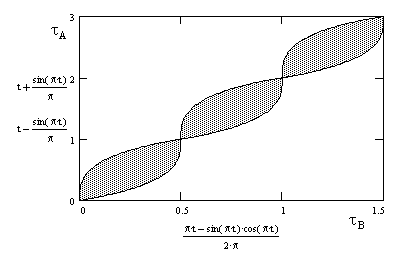
The corresponding plot of proper time relations is shown below.

Notice that the proper time of path B is asymptotically one half of the proper time of path A. (Is there an analogy between this fraction and the relativistic spin 1/2 of particles such as electrons?)

The optimum solution can be compared with other forms. For example, suppose we consider hyperbolic paths of constant proper acceleration. The general form of such a path, passing through x = 0 at t = 0 and t = 1, is

for some fixed parameter k. Solving this for x gives

Inserting this into the invariant area formula and integrating gives

To find the maximum area we differentiate this with respect to k and set the result to zero, giving the condition

Numerically the solution is k = 0.54195612..., corresponding to an invariant area of 0.3098168..., slightly less than the absolute maximum of 1/π = 0.318309...

Return to MathPages Main Menu