The Shape of Coincidence
Two discrete independent events A and B occur during the time interval
t = 0 to T. We can represent their joint occurrence by a point in a
TxT square, where one axis is the time of occurrence of event A and
the other is the time of occurrence of event B. The region of this
square that represents the cases in which A and B occurred within d
of each other is the region surrounding the diagonal, as shown below.
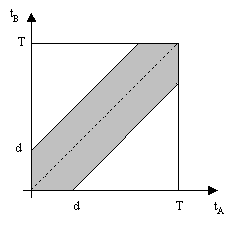 Disregarding the "clipping" at the boundaries, this "region of
coincidence" (within +-d of the diagonal) is simply the region swept
out by a line segment of length d*sqrt(2) normal to the main diagonal.
Therefore, we say the cross-section of the region of coincidences of
degree d is a simple line segment of length d*sqrt(2). We will call
this the "shape" of 2D coincidences.
Coincidences of degree d between THREE events can be represented by
the region near the main diagonal of a TxTxT cube. The region of
coincidences is swept out by a regular hexagon normal to the main
diagonal, so the "shape" of a three-event coincidence is a hexagon,
with edge length d*sqrt(2/3).
In general, given a unit "cube" in n dimensions with n orthogonal
coordinates X1, X2, ...,Xn, we can consider the region of the cube's
content ("volume") consisting of points with coordinates [x1,x2,...,xn]
such that
|xi - xj| < q for all i,j (2)
This can be viewed as the region swept out by a particular n-1
dimensional object as it translates along the diagonal of the unit
cube. Since the solid is in the (n-1)-dimensional "plane" normal to
the diagonal, the coordinates of the solid when it is located at the
origin satisfy
x1 + x2 + ... + xn = 0 (3)
I believe the "volume" of this object is sqrt(n) q^(n-1), although I
have proven it only for the cases n= 2, 3, and 4.
The n-1 dimensional locus satisfying (2) and (3) can be determined
geometrically by considering the vertices. Condition (2) for any
i,j with i!=j implies an n-2 dimensional "face" of the convex poly-
tope, and the absolute value allows two opposite faces for each
such i,j. Thus, the figure has n(n-1) faces. It can also be shown
that the number of vertices for the general n-dimensional case
is 2^n - 2.
Points that lie on more than one face are considered to be on an
"edge", and points that are on a maximal number of faces (meaning
there is no path from such a point to any other face without leaving
one of the faces it is already on) are the vertices of the polytope.
The convexity of the polytope with these vertices is easy to see.
As an example, the six vertices of the sweeping object in the n=3
case can be expressed in terms of multiples of q/n as follows:
[2,-1,-1] [-2,1,1]
[-1,2,-1] [1,-2,1]
[-1,-1,2] [1,1,-2]
By rotating these points into a single 2d plane we arrive at the
regular hexagon. Similarly for the case n=4, the fourteen vertices
correspond to
[3,-1,-1,-1] [-3,1,1,1]
[-1,3,-1,-1] [1,-3,1,1]
[-1,-1,3,-1] [1,1,-3,1]
[-1,-1,-1,3] [1,1,1,-3]
[2,2,-2,-2] [-2,-2,2,2]
[2,-2,2,-2] [-2,2,-2,2]
[2,-2,-2,2] [-2,2,2,-2]
These fourteen vertices can be rotated into a 3d space, showing that
they form the vertices of a solid with 12 identical diamond-shaped
faces. One way of visualizing this solid is to begin with a unit 3d
cube and construct an "Egyptian" pyramid on each face such that the
faces of the adjascent pyramids are flush. The volume of this solid
is 2q^3.
Disregarding the "clipping" at the boundaries, this "region of
coincidence" (within +-d of the diagonal) is simply the region swept
out by a line segment of length d*sqrt(2) normal to the main diagonal.
Therefore, we say the cross-section of the region of coincidences of
degree d is a simple line segment of length d*sqrt(2). We will call
this the "shape" of 2D coincidences.
Coincidences of degree d between THREE events can be represented by
the region near the main diagonal of a TxTxT cube. The region of
coincidences is swept out by a regular hexagon normal to the main
diagonal, so the "shape" of a three-event coincidence is a hexagon,
with edge length d*sqrt(2/3).
In general, given a unit "cube" in n dimensions with n orthogonal
coordinates X1, X2, ...,Xn, we can consider the region of the cube's
content ("volume") consisting of points with coordinates [x1,x2,...,xn]
such that
|xi - xj| < q for all i,j (2)
This can be viewed as the region swept out by a particular n-1
dimensional object as it translates along the diagonal of the unit
cube. Since the solid is in the (n-1)-dimensional "plane" normal to
the diagonal, the coordinates of the solid when it is located at the
origin satisfy
x1 + x2 + ... + xn = 0 (3)
I believe the "volume" of this object is sqrt(n) q^(n-1), although I
have proven it only for the cases n= 2, 3, and 4.
The n-1 dimensional locus satisfying (2) and (3) can be determined
geometrically by considering the vertices. Condition (2) for any
i,j with i!=j implies an n-2 dimensional "face" of the convex poly-
tope, and the absolute value allows two opposite faces for each
such i,j. Thus, the figure has n(n-1) faces. It can also be shown
that the number of vertices for the general n-dimensional case
is 2^n - 2.
Points that lie on more than one face are considered to be on an
"edge", and points that are on a maximal number of faces (meaning
there is no path from such a point to any other face without leaving
one of the faces it is already on) are the vertices of the polytope.
The convexity of the polytope with these vertices is easy to see.
As an example, the six vertices of the sweeping object in the n=3
case can be expressed in terms of multiples of q/n as follows:
[2,-1,-1] [-2,1,1]
[-1,2,-1] [1,-2,1]
[-1,-1,2] [1,1,-2]
By rotating these points into a single 2d plane we arrive at the
regular hexagon. Similarly for the case n=4, the fourteen vertices
correspond to
[3,-1,-1,-1] [-3,1,1,1]
[-1,3,-1,-1] [1,-3,1,1]
[-1,-1,3,-1] [1,1,-3,1]
[-1,-1,-1,3] [1,1,1,-3]
[2,2,-2,-2] [-2,-2,2,2]
[2,-2,2,-2] [-2,2,-2,2]
[2,-2,-2,2] [-2,2,2,-2]
These fourteen vertices can be rotated into a 3d space, showing that
they form the vertices of a solid with 12 identical diamond-shaped
faces. One way of visualizing this solid is to begin with a unit 3d
cube and construct an "Egyptian" pyramid on each face such that the
faces of the adjascent pyramids are flush. The volume of this solid
is 2q^3.
 This 12-faced solid is known as Kepler's Rhombic Dodecahedron. This
fascinating shape has many interesting properties in addition to being
the "shape of coincidence" for four events. If your browser supports
Javascript, you can see an animated view of this polyhedron by
clicking here.
It's interesting that this solid can be said to "duplicate the cube",
reminiscent of the classical Greek problem of constructing a cube with
twice the volume of a given cube. This volume also appears as the
correction term in the case n=3. Note that dimensions 3 and 4 are
the only two dimensions for which the correction term for one is the
sweeping volume for the other.
This 12-faced solid is known as Kepler's Rhombic Dodecahedron. This
fascinating shape has many interesting properties in addition to being
the "shape of coincidence" for four events. If your browser supports
Javascript, you can see an animated view of this polyhedron by
clicking here.
It's interesting that this solid can be said to "duplicate the cube",
reminiscent of the classical Greek problem of constructing a cube with
twice the volume of a given cube. This volume also appears as the
correction term in the case n=3. Note that dimensions 3 and 4 are
the only two dimensions for which the correction term for one is the
sweeping volume for the other.
Return to MathPages Main Menu
 Disregarding the "clipping" at the boundaries, this "region of
coincidence" (within +-d of the diagonal) is simply the region swept
out by a line segment of length d*sqrt(2) normal to the main diagonal.
Therefore, we say the cross-section of the region of coincidences of
degree d is a simple line segment of length d*sqrt(2). We will call
this the "shape" of 2D coincidences.
Coincidences of degree d between THREE events can be represented by
the region near the main diagonal of a TxTxT cube. The region of
coincidences is swept out by a regular hexagon normal to the main
diagonal, so the "shape" of a three-event coincidence is a hexagon,
with edge length d*sqrt(2/3).
In general, given a unit "cube" in n dimensions with n orthogonal
coordinates X1, X2, ...,Xn, we can consider the region of the cube's
content ("volume") consisting of points with coordinates [x1,x2,...,xn]
such that
|xi - xj| < q for all i,j (2)
This can be viewed as the region swept out by a particular n-1
dimensional object as it translates along the diagonal of the unit
cube. Since the solid is in the (n-1)-dimensional "plane" normal to
the diagonal, the coordinates of the solid when it is located at the
origin satisfy
x1 + x2 + ... + xn = 0 (3)
I believe the "volume" of this object is sqrt(n) q^(n-1), although I
have proven it only for the cases n= 2, 3, and 4.
The n-1 dimensional locus satisfying (2) and (3) can be determined
geometrically by considering the vertices. Condition (2) for any
i,j with i!=j implies an n-2 dimensional "face" of the convex poly-
tope, and the absolute value allows two opposite faces for each
such i,j. Thus, the figure has n(n-1) faces. It can also be shown
that the number of vertices for the general n-dimensional case
is 2^n - 2.
Points that lie on more than one face are considered to be on an
"edge", and points that are on a maximal number of faces (meaning
there is no path from such a point to any other face without leaving
one of the faces it is already on) are the vertices of the polytope.
The convexity of the polytope with these vertices is easy to see.
As an example, the six vertices of the sweeping object in the n=3
case can be expressed in terms of multiples of q/n as follows:
[2,-1,-1] [-2,1,1]
[-1,2,-1] [1,-2,1]
[-1,-1,2] [1,1,-2]
By rotating these points into a single 2d plane we arrive at the
regular hexagon. Similarly for the case n=4, the fourteen vertices
correspond to
[3,-1,-1,-1] [-3,1,1,1]
[-1,3,-1,-1] [1,-3,1,1]
[-1,-1,3,-1] [1,1,-3,1]
[-1,-1,-1,3] [1,1,1,-3]
[2,2,-2,-2] [-2,-2,2,2]
[2,-2,2,-2] [-2,2,-2,2]
[2,-2,-2,2] [-2,2,2,-2]
These fourteen vertices can be rotated into a 3d space, showing that
they form the vertices of a solid with 12 identical diamond-shaped
faces. One way of visualizing this solid is to begin with a unit 3d
cube and construct an "Egyptian" pyramid on each face such that the
faces of the adjascent pyramids are flush. The volume of this solid
is 2q^3.
Disregarding the "clipping" at the boundaries, this "region of
coincidence" (within +-d of the diagonal) is simply the region swept
out by a line segment of length d*sqrt(2) normal to the main diagonal.
Therefore, we say the cross-section of the region of coincidences of
degree d is a simple line segment of length d*sqrt(2). We will call
this the "shape" of 2D coincidences.
Coincidences of degree d between THREE events can be represented by
the region near the main diagonal of a TxTxT cube. The region of
coincidences is swept out by a regular hexagon normal to the main
diagonal, so the "shape" of a three-event coincidence is a hexagon,
with edge length d*sqrt(2/3).
In general, given a unit "cube" in n dimensions with n orthogonal
coordinates X1, X2, ...,Xn, we can consider the region of the cube's
content ("volume") consisting of points with coordinates [x1,x2,...,xn]
such that
|xi - xj| < q for all i,j (2)
This can be viewed as the region swept out by a particular n-1
dimensional object as it translates along the diagonal of the unit
cube. Since the solid is in the (n-1)-dimensional "plane" normal to
the diagonal, the coordinates of the solid when it is located at the
origin satisfy
x1 + x2 + ... + xn = 0 (3)
I believe the "volume" of this object is sqrt(n) q^(n-1), although I
have proven it only for the cases n= 2, 3, and 4.
The n-1 dimensional locus satisfying (2) and (3) can be determined
geometrically by considering the vertices. Condition (2) for any
i,j with i!=j implies an n-2 dimensional "face" of the convex poly-
tope, and the absolute value allows two opposite faces for each
such i,j. Thus, the figure has n(n-1) faces. It can also be shown
that the number of vertices for the general n-dimensional case
is 2^n - 2.
Points that lie on more than one face are considered to be on an
"edge", and points that are on a maximal number of faces (meaning
there is no path from such a point to any other face without leaving
one of the faces it is already on) are the vertices of the polytope.
The convexity of the polytope with these vertices is easy to see.
As an example, the six vertices of the sweeping object in the n=3
case can be expressed in terms of multiples of q/n as follows:
[2,-1,-1] [-2,1,1]
[-1,2,-1] [1,-2,1]
[-1,-1,2] [1,1,-2]
By rotating these points into a single 2d plane we arrive at the
regular hexagon. Similarly for the case n=4, the fourteen vertices
correspond to
[3,-1,-1,-1] [-3,1,1,1]
[-1,3,-1,-1] [1,-3,1,1]
[-1,-1,3,-1] [1,1,-3,1]
[-1,-1,-1,3] [1,1,1,-3]
[2,2,-2,-2] [-2,-2,2,2]
[2,-2,2,-2] [-2,2,-2,2]
[2,-2,-2,2] [-2,2,2,-2]
These fourteen vertices can be rotated into a 3d space, showing that
they form the vertices of a solid with 12 identical diamond-shaped
faces. One way of visualizing this solid is to begin with a unit 3d
cube and construct an "Egyptian" pyramid on each face such that the
faces of the adjascent pyramids are flush. The volume of this solid
is 2q^3.
 This 12-faced solid is known as Kepler's Rhombic Dodecahedron. This
fascinating shape has many interesting properties in addition to being
the "shape of coincidence" for four events. If your browser supports
Javascript, you can see an animated view of this polyhedron by
clicking here.
It's interesting that this solid can be said to "duplicate the cube",
reminiscent of the classical Greek problem of constructing a cube with
twice the volume of a given cube. This volume also appears as the
correction term in the case n=3. Note that dimensions 3 and 4 are
the only two dimensions for which the correction term for one is the
sweeping volume for the other.
This 12-faced solid is known as Kepler's Rhombic Dodecahedron. This
fascinating shape has many interesting properties in addition to being
the "shape of coincidence" for four events. If your browser supports
Javascript, you can see an animated view of this polyhedron by
clicking here.
It's interesting that this solid can be said to "duplicate the cube",
reminiscent of the classical Greek problem of constructing a cube with
twice the volume of a given cube. This volume also appears as the
correction term in the case n=3. Note that dimensions 3 and 4 are
the only two dimensions for which the correction term for one is the
sweeping volume for the other.