Golf Tournaments, Polyhedra, and Latin Squares
Suppose we need to schedule 32 golfers into foursomes for five rounds
of a tournament, in such a way that no one is in the same foursome with
anyone else more than once. This is not too hard, because we have
enough players to easily avoid repeated pairings. For example, we can
use the simple pattern shown below, where the first round has the 32
players listed horizontally, the second round has them listed vertically,
and the subsequent rounds skew the successive columns of the vertical
listing by 1, 2, and 3 rows per column, respectively.
Four- Round
some 1 2 3 4 5
----- ----------- ----------- ----------- ----------- -----------
1 1 2 3 4 1 9 17 25 1 16 23 30 1 15 21 27 1 14 19 32
2 5 6 7 8 2 10 18 26 2 9 24 31 2 16 22 28 2 15 20 25
3 9 10 11 12 3 11 19 27 3 10 17 32 3 9 23 29 3 16 21 26
4 13 14 15 16 4 12 20 28 4 11 18 25 4 10 24 30 4 9 22 27
5 17 18 19 20 5 13 21 29 5 12 19 26 5 11 17 31 5 10 23 28
6 21 22 23 24 6 14 22 30 6 13 20 27 6 12 18 32 6 11 24 29
7 25 26 27 28 7 15 23 31 7 14 21 28 7 13 19 25 7 12 17 30
8 29 30 31 32 8 16 24 32 8 15 22 29 8 14 20 26 8 13 18 31
However, suppose we have only 24 players, instead of 32. This is a
bit more challenging, since we have to work harder to avoid repeated
pairings. This is a standard problem in combinatorial design. One
simple approach would be to start with four pair-wise orthogonal
latin squares of size 5x5. (For any prime power N there exist
N-1 pairwise orthogonal Latin squares of size NxN.)
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
1 2 3 4 0 2 3 4 0 1 3 4 0 1 2 4 0 1 2 3
2 3 4 0 1 4 0 1 2 3 1 2 3 4 0 3 4 0 1 2
3 4 0 1 2 1 2 3 4 0 4 0 1 2 3 2 3 4 0 1
4 0 1 2 3 3 4 0 1 2 2 3 4 0 1 1 2 3 4 0
Here we've used the integers (mod 5), and the values of the
kth array for k=1,2,3,4 are given by
A_k(i,j) = k (i-1) + (j-1) (mod 5)
for i,j = 1,2,3,4,5. These arrays are called "latin squares" because
each element appears exacly once in each row and column. They are
said to be "pairwise orthogonal" because if you super-impose one on
top of the other you get all 25 distinct combinations (i,j) with
i,j = 0,1,2,3,4. In other words, each element of one array matches
up with each element of the other array exactly once.
So, if we let the elements of the first array represent the first five
players, and the elements of the second array represent the next five
players, and so on, we can create 25 foursomes from the 20 players
by superimposing the four arrays. Since the arrays are pairwise
orthogonal, we are assured that no one plays in a foursome with the
same person twice.
But we actually need 30 foursomes involving 24 players. This can be
done by mixing in four more players, taking advantage of the fact that
none of the five players in a given array have yet played with each
other. Thus, numbering the players 1 through 24, we have the following
five days worth of foursomes. Each of the 24 players plays once per
day, and no one plays with the same person twice.
Four-
some Day 1 Day 2 Day 3 Day 4 Day 5
---- ----------- ----------- ----------- ----------- -----------
1 1 6 11 16 22 8 14 20 3 10 12 19 4 7 15 18 5 9 13 17
2 2 7 12 17 23 9 15 16 4 24 13 20 5 8 24 19 1 10 14 23
3 3 8 13 18 24 10 11 17 5 21 14 16 1 9 21 20 2 6 15 24
4 4 9 14 19 5 6 12 18 1 22 15 17 2 10 22 16 3 7 11 22
5 5 10 15 20 21 7 13 19 2 23 11 18 3 6 23 17 4 8 12 21
6 21 22 23 24 1 2 3 4 6 7 8 9 11 12 13 14 16 18 19 20
This is good, but we can do even better. It's possible to schedule 24
players into foursomes for SEVEN days in such a way that no two players
are in the same foursome twice. Obviously this means each player is
matched with 21 other players, so he is never matched with 3 of the
others. This partitions the players into eight groups of 3, consisting
of those who never play together. For convenience, let's say these
exclusion groups are i,i+8,i+16 modulo 24 for i=1 to 8. Our arrangement
will be symmetrical in these sets. Now, the players 1, 9, 17 never
play together, so we can put them in foursomes #1, #2, and #3 respectively
on each of the seven days. Then we can fill in the other 21 players
in Foursome #1 in such a way we can create foursomes #2 and #3 simply
by adding 8 (modulo 24) to each player of the preceding foursome.
Then we can create Foursome #4 using just the 21 players, excluding
players 1, 9, and 17, in such a way that (again) Foursomes #5 and #6
are simply the preceding foursome incrementd by 8 (mod 24). The
result is summarized below:
Foursome
Day 1 2 3 4 5 6
--- --------- --------- ---------- -------- ---------- -----------
1 1 2 11 21 9 10 19 5 17 18 3 13 4 7 6 24 8 12 14 15 16 20 22 23
2 1 3 12 22 9 11 20 6 17 19 4 14 5 8 7 18 2 13 15 16 10 21 23 24
3 1 4 13 23 9 12 21 7 17 20 5 15 6 2 8 19 3 10 14 16 11 18 22 24
4 1 5 14 24 9 13 22 8 17 21 6 16 7 3 2 20 4 10 11 15 12 18 19 23
5 1 6 15 18 9 14 23 2 17 22 7 10 8 4 3 21 5 11 12 16 13 19 20 24
6 1 7 16 19 9 15 24 3 17 23 8 11 2 5 4 22 6 10 12 13 14 18 20 21
7 1 8 10 20 9 16 18 4 17 24 2 12 3 6 5 23 7 11 13 14 15 19 21 22
For another interesting problem, suppose you're planning a golf tournament
in which 12 players will each play one round per day for 4 days. You
need to decide how to split up the 12 players into 3 foursomes each
day, and you want to choose the foursomes to minimize the number of
repeated pairings. Ideally you'd like to have each pair of players
placed together in the same foursome only once, but that's obviously
not possible with the conditions of this problem, so the objective
is to minimize the repeated pairings AND to make the schedule as
symmetrical as possible for the 12 players. What's the "best" (most
equally distributed) solution?
In this case it isn't obvious, a priori, how to even precisely
characterize the "best" solution, because minimizing the number
of repeated pairs doesn't necessarily give a symmetrical solution.
One approach is to think of a fairly symmetrical polyhedron with
suitable properties. The rhombic dodecahedron comes to mind,
because it has 12 faces, each of which has 4 neighbors, and there
are 3 dual pairs of mutually exclusive partitions of the 12 faces
into three sets of four. Here's the graph of this solid
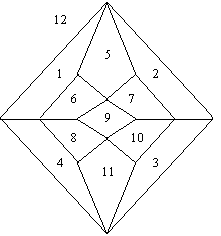 The only pairs of faces whose sets of neighbors are mutually
exclusive are [(1,10),(2,8)], [(3,6),(4,7)], [(5,11),(9,12)].
The largest number of faces that are all mutually non-neighbors
is four, and each face is a member of exactly three such sets.
This gives the partitions
1 2 8 10 1 2 9 11 1 3 7 8
3 4 5 9 3 4 6 7 2 4 6 10
6 7 11 12 5 8 10 12 5 9 11 12
To give a 4th partition, notice that "1" and "10" are each already
paired twice with "2" and twice with "8", and these are the dual sets
of opposite faces [(1,10),(2,8)]. Also, the opposite faces "1" and
"10" are already paired once with each other. Similar pairings exist
for the other two dual sets. This suggests that we create three new
foursomes by combining non-dual pairs. There are eight distinct ways
of doing this. For example, if we combine (1,10) with (4,7), and
combine (2,8) with (9,12), and so on, we have
1 4 7 10
2 8 9 12
3 5 6 11
Using this partition for the 4th round, each player's schedule
includes four "doubles" and four "singles". No two people are on
the same foursome more than twice, and each person plays (at least
once) with exactly 8 (of the 11) other players. Is this the best
that can be done?
The only pairs of faces whose sets of neighbors are mutually
exclusive are [(1,10),(2,8)], [(3,6),(4,7)], [(5,11),(9,12)].
The largest number of faces that are all mutually non-neighbors
is four, and each face is a member of exactly three such sets.
This gives the partitions
1 2 8 10 1 2 9 11 1 3 7 8
3 4 5 9 3 4 6 7 2 4 6 10
6 7 11 12 5 8 10 12 5 9 11 12
To give a 4th partition, notice that "1" and "10" are each already
paired twice with "2" and twice with "8", and these are the dual sets
of opposite faces [(1,10),(2,8)]. Also, the opposite faces "1" and
"10" are already paired once with each other. Similar pairings exist
for the other two dual sets. This suggests that we create three new
foursomes by combining non-dual pairs. There are eight distinct ways
of doing this. For example, if we combine (1,10) with (4,7), and
combine (2,8) with (9,12), and so on, we have
1 4 7 10
2 8 9 12
3 5 6 11
Using this partition for the 4th round, each player's schedule
includes four "doubles" and four "singles". No two people are on
the same foursome more than twice, and each person plays (at least
once) with exactly 8 (of the 11) other players. Is this the best
that can be done?
Return to MathPages Main Menu
 The only pairs of faces whose sets of neighbors are mutually
exclusive are [(1,10),(2,8)], [(3,6),(4,7)], [(5,11),(9,12)].
The largest number of faces that are all mutually non-neighbors
is four, and each face is a member of exactly three such sets.
This gives the partitions
1 2 8 10 1 2 9 11 1 3 7 8
3 4 5 9 3 4 6 7 2 4 6 10
6 7 11 12 5 8 10 12 5 9 11 12
To give a 4th partition, notice that "1" and "10" are each already
paired twice with "2" and twice with "8", and these are the dual sets
of opposite faces [(1,10),(2,8)]. Also, the opposite faces "1" and
"10" are already paired once with each other. Similar pairings exist
for the other two dual sets. This suggests that we create three new
foursomes by combining non-dual pairs. There are eight distinct ways
of doing this. For example, if we combine (1,10) with (4,7), and
combine (2,8) with (9,12), and so on, we have
1 4 7 10
2 8 9 12
3 5 6 11
Using this partition for the 4th round, each player's schedule
includes four "doubles" and four "singles". No two people are on
the same foursome more than twice, and each person plays (at least
once) with exactly 8 (of the 11) other players. Is this the best
that can be done?
The only pairs of faces whose sets of neighbors are mutually
exclusive are [(1,10),(2,8)], [(3,6),(4,7)], [(5,11),(9,12)].
The largest number of faces that are all mutually non-neighbors
is four, and each face is a member of exactly three such sets.
This gives the partitions
1 2 8 10 1 2 9 11 1 3 7 8
3 4 5 9 3 4 6 7 2 4 6 10
6 7 11 12 5 8 10 12 5 9 11 12
To give a 4th partition, notice that "1" and "10" are each already
paired twice with "2" and twice with "8", and these are the dual sets
of opposite faces [(1,10),(2,8)]. Also, the opposite faces "1" and
"10" are already paired once with each other. Similar pairings exist
for the other two dual sets. This suggests that we create three new
foursomes by combining non-dual pairs. There are eight distinct ways
of doing this. For example, if we combine (1,10) with (4,7), and
combine (2,8) with (9,12), and so on, we have
1 4 7 10
2 8 9 12
3 5 6 11
Using this partition for the 4th round, each player's schedule
includes four "doubles" and four "singles". No two people are on
the same foursome more than twice, and each person plays (at least
once) with exactly 8 (of the 11) other players. Is this the best
that can be done?