Smallest Quad With Integer Sides, Perp Diags
What is the area of the smallest quadrilateral whose sides
are all different integers and whose diagonals are perpendicular?
Since the diagonals are perpindicular we can place the
quadrilateral on an xy coordinate system as shown below.
|
|(0,y2)
/|\
/ | \
/ | \
B/ | \A A^2 = x1^2 + y2^2
/ | \
_______/_____|__________\_______ B^2 = y2^2 + x3^2
(x3,0)\ | /(x1,0)
\ | / C^2 = x3^2 + y4^2
\ | /
C\ | /D D^2 = y4^2 + x1^2
\ | /
\|/
|(0,y4)
|
The Pythagorean equations imply
A^2 + C^2 = B^2 + D^2 = x1^2 + y2^2 + x3^2 + y4^2
where A,B,C,D are distinct integers. Thus we need an integer
expressible as a sum of two distinct squares in two ways. By
Fermat's two-square theorem it follows that the smallest occurrance
is the product of the first two primes of the form 4k+1. These
primes are 5 and 13, and the number is 65 = 1^2 + 8^2 = 4^2 + 7^2.
This lets us assign to A,B,C,D the absolute values 1, 4, 8, and 7,
respectively.
Of course, the lengths of the four sides of a quadralateral do
not uniquely determine its shape. Moreover, even if we impose
the requirement that the diagonals are perpendicular, it still
doesn't uniquely determine the shape (and therefore the area).
We essentially have one degree of freedom.
It's also worth noting that the question didn't say the quadri-
lateral had to be convex, so the corners don't all have to bend
outward. Furthermore, the question didn't say the edges of the
quadrilateral can't cross, so it doesn't rule out a "figure 8"
shape. This is important because the definition of the "enclosed
area" of a plane closed curve or polygon reverses the sign when
lines cross. Thus, the absolute area of the figure 8 is zero
(because one loop is positive and the other is negative).
In general the signed area of a quadrilateral with the four vertices
(x1,y1), (x2,y2), (x3,y3), (x4,y4) is given by
1
Area = --- [(x1y2-x2y1)+(x2y3-x3y2)+(x3y4-x4y3)+(x4y1-x1y4)]
2
The vertices of our figure are (x1,0), (0,y2), (x3,0), (0,y4)
so the area is
1
Area = - [x1y2 - x3y2 + x3y4 - x1y4] = (x1-x3)(y2-y4)/2
2
Remember that we have
___________ ___________
y2 = / A^2 - x1^2 y4 = / D^2 - x1^2
so this gives the derivatives
d y2 ___________
---- = - x1 / / A^2 - x1^2 = - x1/y2
d x1
d y4 ___________
---- = - x1 / / D^2 - x1^2 = - x1/y4
d x1
Similarly we have
__________________
x3 = / B^2 - A^2 + x1^2
from which it follows that
d x3
---- = x1/x3
d x1
Therefore, letting apostrophes signify derivatives with respect
to x1, we can different the (double) area with respect to x1 to
give
d Area
2 ------ = (x1-x3)(y2' - y4') + (y2-y4)(1-x3')
d x1
= (x1-x3)( x1/y4 - x1/y2 ) + (y2-y4)(1 - x1/x3)
_ _
| |
= x1 |(x1-x3)(1/y4 - 1/y2) + (y2-y4)(1/x1 - 1/x3) |
|_ _|
= (x1) (2 Area) [ 1/(y2y4) +- 1/(x1x3) ]
We've inserted the +- sign in the last expression to reflect the fact
that we can reverse the signs of any one of the arguments independently
of the others. This derivative vanishes (for non-zero x1 and Area) if
and only if y2y4 = +-x1x3, corresponding to a maximum or a minimum
depending on the signs of the arguments. In either case we have
__________ __________
y2 y4 /A^2 - x1^2 /D^2 - x1^2
x1 = ------- = -----------------------------
x3 _________________
/ B^2 - A^2 + x1^2
Squaring both sides, cancelling terms, and solving for x1 gives
the result
AD
x1 = +- -------------
___________
/ B^2 + D^2
Taking A=1, B=4, C=8, and D=7, we can now compute x1, which then
gives the remaining values
x1 = +-7/sqrt(65)
y2 = +-4/sqrt(65)
x3 = +-32/sqrt(5)
y4 = +-56/sqrt(5)
and then substitute into the area equation (x1-x3)(y2-y4)/2 to give
the result. If we give x1 and x3 opposite signs we have the maximum
possible area for a quadrilateral with sides 1,4,8,7:
|area_max| = (1/2)(60)(39)/65 = 18
and if we give x1 and x3 the same signs we have the minimum possible
magnitude of signed area for a quadrilateral with sides 1,4,8,7:
|signed_area_min| = (1/2)(52)(25)/65 = 10
Notice that this minimum quadrilateral is not convex, and has edges
that cross each other, are shown below
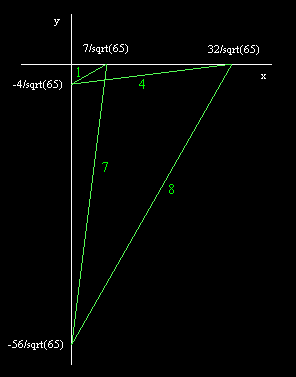The areas of regions enclosed by clockwise and counter-clockwise
paths as we traverse the loop P1,P2,P3,P4,P1 are given opposite
signs, in accord with the definition of signed area. On the other
hand, if we prohibit the corssing of edges, or insist on considering
only unsigned area, then the minimum configurations are when the
shortest edge collapse on one of its neighboring edges, leaving us
with either a 3,7,8 triangle or a 4,6,8 triangle, with areas of
6sqrt(3)=10.39 and 3sqrt(15)=11.62 respectively.
Return to MathPages Main Menu