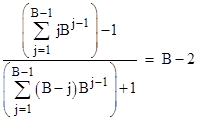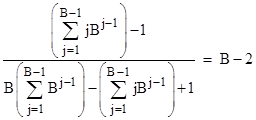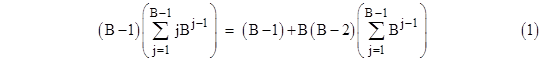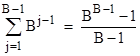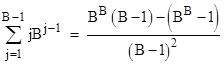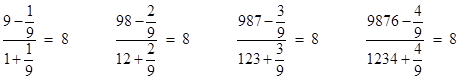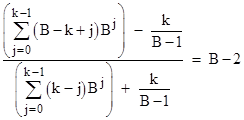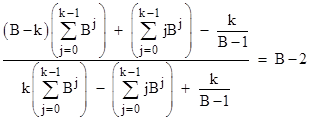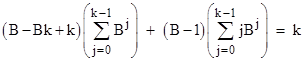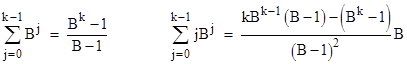|
Ascending and Descending Digits |
|
|
|
He looked so immaculately frightful |
|
As he bummed a cigarette, |
|
Then he went off sniffing drainpipes |
|
And reciting the alphabet. |
|
Bob Dylan |
|
|
|
The decimal number 987654321 is very close to being 8 times the integer 123456789. In fact, we have the exact ratio |
|
|
|
|
|
|
|
The prime factorization of the denominator is (2)(5)(37)(333667). A similar relation holds for any other base. In general, letting B denote the base, we have the algebraic identity |
|
|
|
|
|
|
|
To prove this, we first split the summation in the denominator into two parts as follows |
|
|
|
|
|
|
|
Re-arranging terms, this can be written as |
|
|
|
|
|
|
|
The summation on the right side of (1) is just the finite geometric series, which has the closed-form expression |
|
|
|
|
|
|
|
A closed-form expression for the summation on the left side of (1) can be found by differentiating the finite geometric series, giving the identity |
|
|
|
|
|
|
|
Substituting for the summations in (1) and multiplying through by (B−1), we get |
|
|
|
|
|
|
|
Equality is confirmed by expanding both sides and cancelling terms. |
|
|
|
This type of relation is not limited to complete sequences of digits. We also have identities involving numbers with truncated strings of digits, such as |
|
|
|
|
|
|
|
and so on. Written explicitly for arbitrary base B and letting k denote the number of digits in each number, these relations have the form |
|
|
|
|
|
|
|
Naturally if we set k = B−1 and shift the index of summation we recover the previous relation. Splitting the summations, this more general relation can be written as |
|
|
|
|
|
|
|
Re-arranging terms, this becomes |
|
|
|
|
|
|
|
The summations have the closed form expressions |
|
|
|
|
|
Making these substitutions and multiplying through by (B−1), we get |
|
|
|
|
|
|
|
Expanding the products and cancelling terms, this confirms the equality. |
|
|