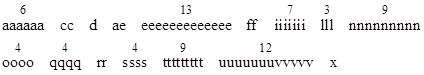|
The Fundamental Anagram of Calculus |
|
|
|
Here's an interesting quote from the correspondence of Isaac Newton: |
|
|
|
|
|
|
|
This is from the 2nd letter that Newton wrote to Leibniz (via Oldenburg) in 1677. He was responding to some questions from Leibniz about his method of infinite series and came close to revealing his "fluxional method" (i.e., calculus), but then decided to conceal it in the form of an anagram. After describing his methods of tangents and handling maxima and minima, he wrote |
|
|
|
The foundations of these operations is evident enough, in fact; but because I cannot proceed with the explanation of it now, I have preferred to conceal it thus: 6accdae13eff7i3l9n4o4qrr4s8t12ux. On this foundation I have also tried to simplify the theories which concern the squaring of curves, and I have arrived at certain general Theorems. |
|
|
|
The anagram expresses, in Newton's terminology, the fundamental theorem of the calculus: "Data aequatione quotcunque fluentes quantitates involvente, fluxiones invenire; et vice versa", which means "Given an equation involving any number of fluent quantities to find the fluxions, and vice versa." Arranging the characters in his Latin sentence in alphabetical order (and assuming he counted the dipthong "ae" as a separate character, and u's and v's are counted as the same character), the number of occurrences of each character are as follows |
|
|
|
|
|
|
|
This agrees with Newton's anagram |
|
|
|
|
|
|
|
except that I count nine t's instead of eight. Possibly Newton's original Latin spelling used one fewer t's, although I can't see which one of them could plausibly be omitted. It could also be that the anagram has been incorrectly copied, but it agrees with the version in both Westfall's and Christianson's biographies, as well as the transcription of Newton's letter contained in Calinger's Classics of Mathematics. Another possibility is that Newton simply mis-counted. This isn't as implausible as it might seem at first, since there is a well-known psychological phenomenon of overlooking the second letter in short connective words (like the f in "of") when quickly counting the number of occurrences of a certain letter in a string of text. It's very easy, when counting the number of t's in Newton's Latin phrase, to neglect the "t" in the word "et". |
|
|
|
Ironically, neither Leibniz nor Newton had published anything on calculus at the time this letter was exchanged, although both are believed to have been in possession of the calculus, so if Newton had just come right out with a complete and explicit statement of his calculus he would have placed Leibniz in a very difficult position, and would have established his own priority beyond doubt (since the letter passed through Oldenburg). Instead, Newton's very protectiveness and secrecy caused him to lose whatever unambiguous claim to priority he might have had (and led to an acrimonious priority dispute that embittered both his and Leibniz's later lives). |
|
|
|
On a very deep level it was natural for Newton to express himself in anagrams, because he seems to have regarded "contrived obscurity" (in Domson's words) as an essential feature of God's design for the world, and Newton adopted this mode of operation in his own work. Recall that he said he had made the Principia "designedly abstruse" (to avoid being baited by "little smatterers" in mathematics). Even more pointedly, Newton spent many years attempting to interpret the prophesies in the Bible, which he believed were presented in deliberately disguised form so that their meaning could only be inferred by solving them like puzzles. Interestingly, he had disdain for people who tried to unravel prophesies of future events. In his view, this was misguided and doomed to failure. He believed the encoded prophesies were intended to be understood only after the fact. In his "Observations upon the Prophecies of the Apocalypse of St. John" he wrote |
|
|
|
The folly of interpreters has been to foretell times and things by this Prophecy, as if God designed to make them Prophets. By this rashness they have not only exposed themselves, but brought Prophecy also into contempt. The design of God was much otherwise. He gave this [Revelations] and the Prophecies of the Old Testament, not to gratify men's curiosities by enabling them to foreknow things, but that after they were fulfilled they might be interpreted by the event, and [that] his own Providence, not the Interpreters, be then manifested thereby to the world. For the event of things predicted many ages before, will then be a convincing argument that the world is governed by Providence. |
|
|
|
We might say that Newton saw the biblical prophesies serving exactly the same function as his anagram on fluxions and fluents, i.e., it is presented in a form that cannot be interpreted to reveal its meaning before the fact, but after the facts have transpired and the solution of the puzzle is found, it can serve as irrefutable evidence of the Providence of the creator. |
|
|