Highly Heronian Ellipses
A triangle with integer edge lengths and integer area is
called "Heronian", after the Greek mathematician Heron.
Such triangles are also sometimes called "rational triangles",
since any triangle with rational edges and area can obviously
be scaled to give one with integer edges and area. Of course,
every ordinary Pythagorean triple (a,b,c) gives a rational
triangle, since the area of this right triangle is simply
ab/2. (For example, the area of the familiar 3,4,5 triangle
is 6.) So, to make things interesting, we usually focus on
triangles that are not right-angled.
Heron noted the example (13,14,15), which has an area of
84. This can easily be computed using Heron's formula for
the area of a general triangle as a function of it's three
edge lengths a,b,c:
1 _____________________________
A = --- /(a+b+c)(-a+b+c)(a-b+c)(a+b-c)
4
It's not hard to find infinite families of such triangles.
For example, in 598 AD Brahmagupta noted that for any integers
a,b,c we have an oblique triangle with edges of length
L1 = (a^2 + b^2) c
L2 = (a^2 + c^2) b
L3 = (a^2 - bc)(b + c)
whose area is A = abc(b+c)(bc-a^2). Gauss (as usual) went further
and found that ALL Heronian triangles have edge lengths that can
essentially be expressed in the form
L1 = 4abfg[a^2 + b^2]
L2 = +-4ab(f+g)(fa^2 - gb^2)
L3 = 4ab[(af)^2 + (bg)^2]
in which case the radius of the circumscribing circle is
R = (a^2 + b^2)[(af)^2 + (bg)^2]
Recall that the area of a triangle is L1*L2*L3/(4R) where R is the
circumscribing radius. Hence the area of Gauss' Heronian triangles
is
A = |16(ab)^3 fg(f+g)(fa^2 - gb^2)|
It may be worth mentioning that if we define
L1 = x + y L2 = x + z L3 = y + z
then from Heron's area formula the triangle is Heronian if an only
if xyz(x+y+z) is a square.
We can also find specialized Heronian triangles. For example,
in 1722 the Japanese mathematician Nakane Genkei gave a recurrence
for an infinite family of triangles with *consecutive* integer
sides and integer areas (although it isn't clear if he completed
the induction).
We'll derive Genkei's result below, but first let's consider
a slightly more general problem, namely, to find the Heronian
triangles whose edges a,b,c are in arithmetic progression, i.e.,
for some integers x and d we have the edge lengths
a = x - d b = x c = x + d
Notice that if x and d have a greatest common factor g, then
g divides each of a, b, and c, which implies that g appears
to the 4th power inside the radical sign in Heron's formula,
so it can be removed from the square root. Thus, g^2 must
divide A, so we need only consider primitive solutions, i.e.,
those with g=1. In other words, we can assume that x and d
have no common factor.
Substituting into Heron's formula gives
____________________
4A = / (3x)(x+2d)(x)(x-2d)
Squaring both sides, we have
(4A)^2 = 3x^2 [(x+2d)(x-2d)]
Since the left side is even, we know that x must be even,
so there is an integer y such that x=2y. Also, by unique
factorization of integers, it's clear from this equation
that the quantity in [] brackets must be 3 times a square,
which means there is an integer m such that
(x+2d)(x-2d) = 3m^2
Since x and d have no common factor, it's clear that the
two factors on the left are coprime except for a possible
common factor of 2 because x=2y. It follows that m must
also be even, so we have an integer n such that m=2n.
With these substitutions we have
y^2 - d^2 = 3n^2
in coprime integers y,d,n, which can be written as
d^2 + 3n^2 = y^2
The general solution of this Diophantine equation is
p^2 - 3q^2 p^2 + 3q^2
|d| = ---------- |n| = pq |y| = ----------
2 2
for odd integers p,q, or double these quantities if p and q
have opposite parity. Therefore, with odd p,q we have
|x| = (p^2 + 3q^2) |d| = (p^2 - 3q^2)/2
For example, with p=q=1 this gives x=4,d=1, leading to the
Pythagorean triangle with edge lengths a=3,b=4,c=5. On the
other hand, if p,q, have opposite parity we have
|x| = 2(p^2 + 3q^2) |d| = (p^2 - 3q^2)
The first example of this type is with p=2,q=1, which gives
x=14, d=1, leading to the original Heronian example a=13,b=14,
c=15. In general, the case with p,q both odd gives
a = (p^2 + 9q^2)/2
b = p^2 + 3q^2 A = 3pq(p^2 + 3q^2)/2
c = 3(p^2 + q^2)/2
whereas if p,q have opposite parity we have
a = p^2 + 9q^2
b = 2p^2 + 6q^2 A = 6pq(p^2 + 3q^2)
c = 3p^2 + 3q^2
Here's a table of all the Heronian triangles with edges in
arithmetic progression and total perimeter less than 1000
given by odd values of p and q:
p q perimeter a b c Area
--- --- --------- ---- ---- ---- ------
1 1 12 5 4 3 6
1 3 84 41 28 15 126
5 -1 84 17 28 39 210
5 3 156 53 52 51 1170
7 1 156 29 52 75 546
-1 5 228 113 76 39 570
7 -3 228 65 76 87 2394
7 5 372 137 124 111 6510
11 1 372 65 124 183 2046
1 7 444 221 148 75 1554
11 -3 444 101 148 195 7326
5 7 516 233 172 111 9030
13 -1 516 89 172 255 3354
11 5 588 173 196 219 16170
13 3 588 125 196 267 11466
13 -5 732 197 244 291 23790
-1 9 732 365 244 123 3294
-5 9 804 377 268 159 18090
11 -7 804 281 268 255 30954
7 9 876 389 292 195 27594
17 -1 876 149 292 435 7446
13 7 948 305 316 327 43134
17 3 948 185 316 447 24174
Notice that, with the exception of the case p=1,q=1, all
the perimeters appear twice. In each case we have (with
an appropriate choice of signs) p + q equal to the same
quantity, and the edge length b is the same for both. These
two solutions correspond to the two roots of the combined
equations p^2 + 3q^2 = b and p + q = n for fixed values
of b and n.
The next solution set with odd p,q has four cases, with a
perimeter of 1092 and b = 364:
p q perimeter a b c Area
--- --- --------- ---- ---- ---- ------
1 11 1092 545 364 183 6006
17 -5 1092 257 364 471 46410
11 9 1092 425 364 303 54054
19 1 1092 185 364 543 10374
This is due to the fact that 1092 is expressible in the form
3(p^2 + 3q^2) in two distinct ways
1092 = 3[(19)^2 + 3(1)^2] = 3[(17)^2 + 3(5)^2]
which is due to the fact that it's divisible by two primes,
7 and 13, congruent to 1 mod 3. These two expressions arise
from the different ways of multiplying out the product
1092/3 = 364 = (2)^2 (91) = 4[7][13]
where
7 = (2)^2 + 3(1)^2 13 = (1)^2 + 3(2)^2
using the ancient product rule for quadratic forms
(x^2 + N y^2)(u^2 + N v^2) = (xu + Nyv)^2 + N(xv - yu)^2
= (xu - Nyv)^2 + N(xv + yu)^2
Thus, each distinct prime factor of the form 3k+1 doubles the
number of distinct solutions (in general). If we divide each
of the perimeters in the above table by 3(4) we find
7 13 19 31 37 43 7^2 61 ...
which are precisely the primes congruent to 1 mod 3 (or
squares of those primes), leading to the two solutions for
each perimeter. When we reach perimeters, like 1092, that
are (12 times) the product of TWO distinct primes congruent
to 1 mod 3, we have 2^2 = 4 distinct solutions. Likewise
when we reach the perimeter 12(7*13*19) = 20748 with THREE
distinct prime factors congruent to 1 mod 3 we expect to
find 2^3 = 8 distinct Heronion triangles with that perimeter,
and in fact we have
p q perimeter a b c Area
--- --- --------- ---- ---- ---- --------
17 47 20748 10085 6916 3747 8288826
79 -15 20748 4133 6916 9699 12293190
83 -3 20748 3485 6916 10347 2583126
37 43 20748 9005 6916 4827 16505034
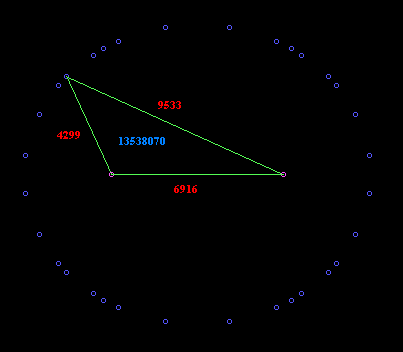
-29 45 20748 9533 6916 4299 13538070
53 -37 20748 7565 6916 6267 20343414
71 25 20748 5333 6916 8499 18413850
73 23 20748 5045 6916 8787 17417946
A geometrical way of looking at this is to imagine a planet in
an elliptical orbit whose eccentricity is 1/2 and such that
the distance between the two foci of the orbit is 6919 units.
If we trace out the locus of points relative to that fixed
line segment such that the sum of the distances from the two
foci is constant, we have an ellipse. Thus we can imagine a
planet following an elliptical path such that the perimeter
of the triangle formed by the planet and the two foci remains
constant at 20748 units. The above solutions are then seen to
determine the locations of 32 "Heronian points" on that ellipse
(because each of the 8 solutions appears in each of the four
quadrants) such that the distances to the two foci are both
integers AND the area of the triangle formed by the foci and
that point is an integer. This is illustrated in the figure
below:
Moving on to the solutions given by values of p,q with opposite
parity, we have the following table of solutions for perimeters
less than 1000:
p q perimeter a b c Area
--- --- --------- ---- ---- ---- --------
2 1 42 13 14 15 84
1 2 78 37 26 15 156
4 1 114 25 38 51 456
2 3 186 85 62 39 1116
5 2 222 61 74 87 2220
4 3 258 97 86 75 3096
1 4 294 145 98 51 1176
7 2 366 85 122 159 5124
8 1 402 73 134 195 3216
5 4 438 169 146 123 8760
2 5 474 229 158 87 4740
8 3 546 145 182 219 13104
4 5 546 241 182 123 10920
7 4 582 193 194 195 16296
10 1 618 109 206 303 6180
1 6 654 325 218 111 3924
10 3 762 181 254 327 22860
11 2 798 157 266 375 17556
5 6 798 349 266 183 23940
8 5 834 289 278 267 33360
2 7 906 445 302 159 12684
7 6 942 373 314 255 39564
4 7 978 457 326 195 27384
In these cases there are half as many solutions as in the
previous cases for any given number of distinct prime divisors
congruent to 1 mod 3, because there is only a single power of
2 in the perimeters. Notice that we get double solutions with
perimeter of 546 and 798, each of which is divisible by two
distinct primes congruent to 1 mod 3. Also, for each perimeter
with a double solution with p+q even, there is a single solution
with half the perimeter with p+q odd.
Anyway, we could specialize still further and consider just
the Heronian triangles whose edge lengths are consecutive
integers (rather than just in arithmetic progression). For
this we need to restrict the value of |d| to be 1. Thus we
have
p^2 - 3q^2 = +-2 if p+q is even
p^2 - 3q^2 = +-1 if p+q is odd
These are Pell equations, and can be solved either by the
continued fraction for sqrt(3) or by recurrences. The give
the infinite families of solutions
p q p q
--- --- --- ---
1 1 2 1
5 3 7 4
19 11 26 15
71 41 97 56
265 153 362 209
etc. etc.
where each sequence of paramaters satisfies the linear
recurrence s[n] = 4s[n-1] - s[n-2]. These sequences give,
alternately, the triangles
p q a b c area
--- --- --- --- --- ---------
1 1 3 4 5 6
2 1 13 14 15 84
5 3 51 52 53 1170
7 4 193 194 195 16296
19 11 723 724 725 226974
26 15 2701 2702 2703 3161340
71 41 10083 10084 10085 44031786
The values of b in this combined sequence satisfy the recurrence
b[n] = 4b[n-1] - b[n-2], and the areas satisfy the recurrence
A[n] = 14A[n-1] - A[n-2].
Return to MathPages Main Menu