Meandering Convergence of a Dirichlet Series
In a previous note we discussed how Leibniz might have anticipated
Euler's summation of the inverse square integers by factoring
the product form of the arctan(1) series. This leads to the
interesting "Dirichlet" series
pi 1 1 1 1 1 1 1 1 1 1
-- = 1 + - - - + - + - + -- - -- - -- - -- + -- + -- + ...
2 3 5 7 9 11 13 15 17 19 21
inf (-1)^f(2j+1)
= SUM ------------
j=0 2j+1
where f(k) is the sum of the exponents of primes congruent to 1
modulo 4 in the prime factorization of k. If we let s(x) denote
the partial sum of this series up to 2j+1 < x we find that it
fairly quickly achieves over 99% of pi/2, but then it meanders
around for a very long time, occassionally coming very close to
pi/2 (from below) and then backing off. (By comparison, the series
for arctan(1) converges FAR more rapidly and uniformly on pi/4.)
Just for fun, I plotted the difference pi/2 - s(x) versus x
for values of x up to 10 million, as shown below:
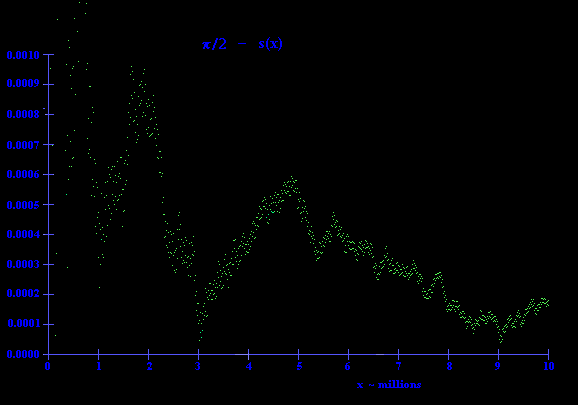 Interestingly, the difference between s(x) and pi/2 dips at about
1/3 million, then again at about 1 million, again at 3 million, and
then again at very close to 9 million. I haven't checked, but it
seems likely that the next near-approach to zero would occur around
27 million, and so on. This seems to suggest that the parity of the
exponents of prime factors congruent to 1 (mod 4) exhibits a distinct
logarithmic periodicity in the sequence of natural numbers.
Is this periodicity genuine? If so, what causes it, and what is
the precise frequency? Also, is it true that pi/2 - s(x) is always
positive? If not, at what value of x does this difference first
go negative?
For another example of this kind of "logarithmic wave" propogating
through the natural numbers, see The Half-Totient Tree.
Interestingly, the difference between s(x) and pi/2 dips at about
1/3 million, then again at about 1 million, again at 3 million, and
then again at very close to 9 million. I haven't checked, but it
seems likely that the next near-approach to zero would occur around
27 million, and so on. This seems to suggest that the parity of the
exponents of prime factors congruent to 1 (mod 4) exhibits a distinct
logarithmic periodicity in the sequence of natural numbers.
Is this periodicity genuine? If so, what causes it, and what is
the precise frequency? Also, is it true that pi/2 - s(x) is always
positive? If not, at what value of x does this difference first
go negative?
For another example of this kind of "logarithmic wave" propogating
through the natural numbers, see The Half-Totient Tree.
Return to MathPages Main Menu
 Interestingly, the difference between s(x) and pi/2 dips at about
1/3 million, then again at about 1 million, again at 3 million, and
then again at very close to 9 million. I haven't checked, but it
seems likely that the next near-approach to zero would occur around
27 million, and so on. This seems to suggest that the parity of the
exponents of prime factors congruent to 1 (mod 4) exhibits a distinct
logarithmic periodicity in the sequence of natural numbers.
Is this periodicity genuine? If so, what causes it, and what is
the precise frequency? Also, is it true that pi/2 - s(x) is always
positive? If not, at what value of x does this difference first
go negative?
For another example of this kind of "logarithmic wave" propogating
through the natural numbers, see The Half-Totient Tree.
Interestingly, the difference between s(x) and pi/2 dips at about
1/3 million, then again at about 1 million, again at 3 million, and
then again at very close to 9 million. I haven't checked, but it
seems likely that the next near-approach to zero would occur around
27 million, and so on. This seems to suggest that the parity of the
exponents of prime factors congruent to 1 (mod 4) exhibits a distinct
logarithmic periodicity in the sequence of natural numbers.
Is this periodicity genuine? If so, what causes it, and what is
the precise frequency? Also, is it true that pi/2 - s(x) is always
positive? If not, at what value of x does this difference first
go negative?
For another example of this kind of "logarithmic wave" propogating
through the natural numbers, see The Half-Totient Tree.