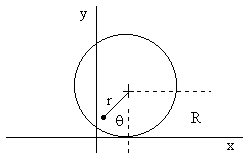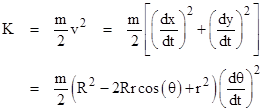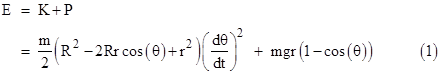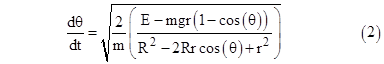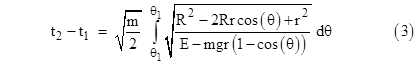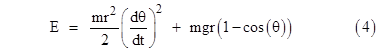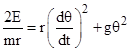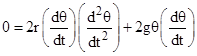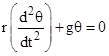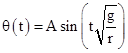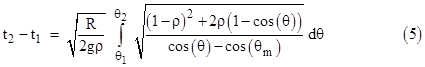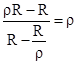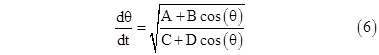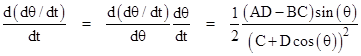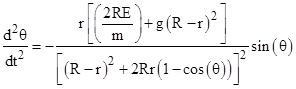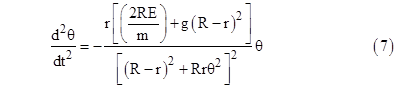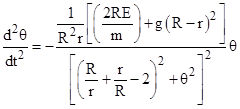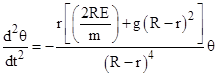Time for a Rocking Chair

Consider a particle of mass m attached at a radial distance r from the center of a massless circular disk of radius R, and suppose the disk is in the xy plane and rolling like a wheel (without slipping) on the x axis, as illustrated below.

The x and y coordinates of the mass particle as functions of the angle θ are

and so the components of the velocity are

Hence the kinetic energy is

Also, the potential energy relative to the configuration at θ = 0 is

where g is the acceleration of gravity (assumed constant).  The total energy

is constant, so we can combine these equations and solve for dθ/dt to give

Thus we have the integral

where ρ = r/R and ε = E/(gmR).  Setting t(0) = 0, we can compute the time required to roll (monotonically) from the position corresponding to θ₁ = 0 to the position corresponding to any desired θ₂ by evaluating this integral.  Of course, if the energy E is small enough, the denominator of the integrand will go to zero for some value of θ.  This means the time required to reach a certain θ goes to infinity, at the point when the disk slows to a stop at its maximum amplitude.  Thereafter it reverses direction.  It follows that the period of one complete cycle is equal to four times the above integral evaluated from θ₁ = 0 to the value of θ₂ = θ_max such that the denominator vanishes, i.e.,

Since the argument of the inverse cosine must be in the range from -1 to +1 (in order for θ_max to be real-valued), this implies that 0 ≤ E/(mgr)  ≤ 2.  In other words, the energy E must satisfy the inequalities 0 ≤ E ≤ 2mgr, which was to be expected, because 2mgr is the potential energy the particle would have at the "12 o'clock" position relative to the potential energy at the "6 o'clock" position.  If the total energy exceeds this value, then it must have some kinetic energy when it reaches the top of the disk, so it will continue to roll, without ever reversing course.

We can consider two generate cases.  First, if r = 0 and R > 0, the integrand in (1) is just a constant, so (setting θ₁ = 0) we immediately have

Since the vertical position is constant in this case, the total energy is just the kinetic energy E = K = mv²/2, so this implies vt = Rθ.  Second, if R = 0 and r > 0, the rolling disk reduces to a stationary pivot point, and the system is a simple pendulum.  In this case equation (1) reduces to

For sufficiently small angular displacements θ, the value of cos(θ) approaches 1 - θ²/2, so we can make this substitution and divide through by mr/2 to give the energy equation of a pendulum for small displacements

Differentiating with respect to time gives

Dividing through by 2(dθ/dt), we arrive at the differential equation

with the solution

which shows that the frequency (for sufficiently small angular displacements) is independent of both the mass and the energy.  The period of the oscillation is

On the other hand, if the angular displacement is not small, we must use equation (4), which can be integrated as shown in equation (3) with R = 0.  For cases when the system's total energy is close to the boundary with non-periodic configurations, the integral is very ill-conditioned (near the top of the disk), but the system can still be evaluated as described in the article on Tilting Pencils.

In the general case, with R > 0 and r > 0, we can define ρ = r/R and ε = E/(mgr), where 0 < ε < 2 in order for the system to be periodic.  For a periodic system the energy parameter ε can be expressed in terms of the maximum angular displacement θ_m as 1 - cos(θ_m), so equation (3) can be written as

Interestingly, this expression is invariant under replacement of ρ with its reciprocal 1/ρ, as can be verified by direct substitution.  This implies that, for a disk of radius R, the time response with a particle of mass m attached at a radius Rρ, when released from a maximum angle θ_m, is identical to the response with the particle attached at a radius R/ρ.

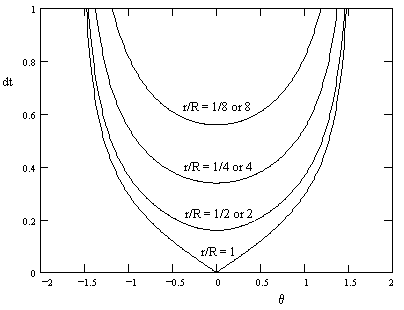
For a disk of unit radius (R = 1) with the mass released from an angle θ_m = π/2, the figure below shows the scaled integrand of (5) as a function of θ, so the time required to rock (and roll) from one angle to another is given by the area under this curve between those two angles.

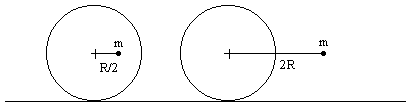
For example, the angular displacement versus time would be identical for the two disks of radius R shown below in their maximum displacement positions.

It may seem surprising that these two systems will rock and roll identically, because the right hand system has four times the potential energy, which means the mass particle must have twice the speed at the "6 o'clock" configuration.  The reason this may be confusing is that the radial arms are in the ration 4:1, so we might think for a given angular speed the right hand particle is moving four times as fast (rather than twice as fast, as required by the energy balance).  However, this confusion is due to overlooking the rolling motion of the disks.  When in the "6 o'clock" positions, the right hand mass particle will indeed be moving at four times the speed of the left hand particle with respect to the disk centers, but the disk centers will be moving in the opposite direction at the geometric mean of those two speeds.  The net effect is that the left and right hand particles will be moving with the total speeds ω(ρR - R) and ω(R/ρ - R) where ω is the angular velocity, so the speed ratio is actually

consistent with the fact that the ratio of potential energies in the static configuration is ρ².

From the plot of dt versus θ we can also determine the period of a complete cycle, equal to the total area under the respective curve.  Therefore, the minimum possible period is for the case ρ = 1, i.e., when the mass particle is on the perimeter of the disk.  In this case the particle actually "bounces" on the rolling surface.

Another approach to this problem is to differentiate the full equation (2) again with respect to time, just as we did in the special case with R = 0, but this time allowing R to be non-zero.  Notice that (2) can be written in the form

where

Differentiating (6) with respect to t gives

Therefore, substituting the expressions for A, B, C, and D, we have

In the small-angle approximation we can substitute θ and θ²/2 for sin(θ) and (1–cos(θ)) respectively, and this becomes

This can be re-written as

which shows that if either R/r or r/R is much greater than 1, the denominator is essentially constant, so we can omit the θ² in the denominator to give the simple harmonic equation

On the other hand, if r and R are of the same order of magnitude, the small-angle motion of such a system is not the same as simple harmonic motion.  For example, if r = R, equation (7) reduces to

which is an "inverse cube" acceleration law, nothing like simple harmonic motion.  In this case the acceleration is infinite at θ = 0, where the impulse "bounce" occurs.

Since the mass component of this system is modeled as just a single point particle, it has no intrinsic angular momentum, but if we spread the mass out over a finite extent, it would have intrinsic angular momentum, which would place limits on the angular acceleration of the disk.  This leads to the well-known problem of the "hopping hoop", in which the massless hoop at some stage pivots around the mass while the mass is still above the surface, so that the hoop effectively "hops".

Return to Table of Contents