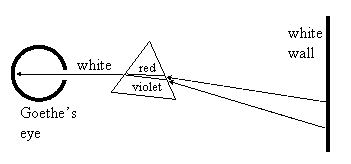Zur Farbenlehre

Every act of seeing leads to consideration, consideration to reflection, reflection to combination, and thus it may be said that in every attentive look on nature we already theorize. But in order to guard against the possible abuse of this abstract view… we should theorize without forgetting that we are so doing, we should theorize with mental self-possession, and, to use a bold word, with irony.

Johann Wolfgang von Goethe is widely regarded (at least among people who read German) as one of the greatest authors and poets of all time, but he himself is said to have valued his scientific work – especially his Theory of Colors – even more highly than his literary creations. Nearly a century before Goethe was born, Isaac Newton had made what he (Newton) described as “the oddest if not the most considerable detection which has hitherto been made in the operations of Nature”. This was Newton’s discovery of the heterogeneity of white light, and the differential refrangibility of its components, i.e., the spectrum of visible colors. At first Newton’s theory of colors engendered spirited opposition and debate among such men as Robert Hooke, Christian Huygens, and others. Indeed, the bitterness that Newton felt at having his treasured discovery publicly challenged led him to eschew any further publication for almost twenty years, and to defer any more publications on optics for even longer. Nevertheless, Newton’s analysis of light and color eventually came to be almost universally accepted, partly on its merits, and partly due to his great prestige as the author of the Principia and the Opticks.

Prior to Newton, the leading theory of colors was “modificationism”, which held that light is modified by passing through a prism. Based on this concept it might be natural to expect that light of any color could be modified (by passing through a glass, for example) into some other colors. Newton’s observations (and theorizing) led him to a different conception of colors. He seems to have been the first person to connect the angular and the chromatic aspects of refraction. He noticed that if a single circular beam of white light is passed through a prism and projected onto a wall, the image is not circular, but elongated, and instead of being white, it is a range from colors, with red at one end and violet at the other. The fact that the circular beam is spread out implied (to Newton) that different parts of the light had been refracted through different angles. The fact that each angular position was a different color suggested to Newton that each of these “spectral” colors was contained within the original white light, and they were separated due to having different “refrangibilities”. Red undergoes the least amount of angular refraction, and violet the most.

After pondering the implications of these observations, Newton thought of a way of testing his thesis. If his conception of color and refraction was correct, then passing a sliver of the spectrum through a second prism should not result in any elongation or color change. The pure spectral color should be refracted by the same amount that it underwent in the first prism. Newton called this the experimentum crucis, because he regarded it as the crucial experimental test of whether a prism produces colors by modification, or by separating pure spectral constituents based on their different refrangibilities. The outcome of this experiment was as Newton expected, i.e., the pure spectral beam did not undergo any elongation through the second prism, its color did not change, and it’s angle of refraction was the same as it had been through the first prism. From this Newton concluded that white light must be composed of all the “pure colors” of the spectrum, and these can be separated by a prism because each color of light has its own “refrangibility”, meaning that each color undergoes a slightly different amount of refraction when passing through a prism. A simplified schematic of Newton’s experiment is shown below.

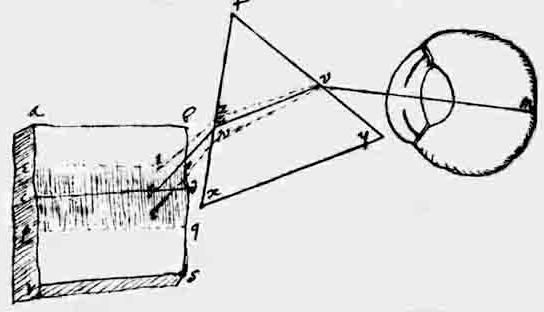
Ironically, the very first recorded evidence of Newton’s concept of differential refrangibility is (according to Westfall) a drawing from 1665 (when Newton was 23 years old), which depicts rays of light emanating from different points on a wall passing through a prism and being refracted differently so they emerge along a single ray, which then enters the eye. In other words, it was the reverse of the observation with which he began his 1672 exposition. The drawing from his notebook is reproduced below.

This reversal would be ironic enough, but the surpassing irony is that the “reverse” situation is precisely the one that, nearly a century later, was also Goethe’s very first observation in the field of colors. And the crowning irony is that this observation led Goethe to exactly the opposite conclusion! In other words, it was this very observation that convinced him that Newton’s theory of colors was completely wrong.

Recall that, in addition to being a great writer, Goethe was also an accomplished painter, so it’s not surprising that he took an interest in colors, although we might have expected his interest to be limited to the psychological and representational aspects of color perception, rather than the physical aspects. Nevertheless, some time around the year 1790 (when he was 41 years old), Goethe began to think about the physics of color.

Like everyone in the world I was convinced that all the colors were contained in light; I had never been told otherwise, and I had never had the slightest reason for doubting it, since I had taken no further interest in the matter… As I was now thinking about approaching colors from the perspective of physics, I read in some compendium or other the customary account, and, since I could not derive anything for my purposes from the theory as it stood there, I undertook at least to see the phenomena for myself…  [Goethe recalled having looked at a prism in his youth, and] I remembered well that everything appeared many-colored, but in what manner was no longer present to my mind. At that very moment I was in a room that had been painted completely white; I expected, mindful of the Newtonian theory as I placed the prism before my eyes, to see the light that comes from there to my eye split up into so many colored lights. How astonished I was, then, when the white wall, observed through the prism, remained white just as before; that only there, where darkness adjoined on it, did a more or less determinate color appear…It did not take much deliberation for me to recognize that a boundary is necessary to produce colors, and I immediately said to myself, as if by instinct, that the Newtonian teaching is false.

This instinctive conviction set Goethe on a campaign to discredit Newton’s optical works. Soon after the epiphany described above, in the early 1790’s, he began work on “Beitrage zur Optik” (Contributions to Optics), in which he presented with very little comment a long series of experiments and observations (such as the one described above) that he evidently believed were de facto refutations of Newton’s theory of colors.

In another ironic turn, Goethe’s main dictum was to spurn theorizing and hypothesizing (activities he associated with Newton), and to adhere scrupulously to the facts of experience. This gives Goethe’s “Beitrage” the sense of being a mere catalogue of experiences rather than a scientific theory. The irony is that, in the previous century, Newton was known for adopting the very same methodological stance, as when he famously asserted “I feign no hypotheses”. Indeed it was the response to his first publication on optics and color that pressed Newton into adopting this policy, although in his case it was perhaps partly a rhetorical facade to shield his hypotheses from criticism, by claiming that they were not hypotheses but demonstrated facts. Of course, one of Goethe’s concerns was precisely the difficulty of distinguishing aspects of our mental representations of things from facts about the things themselves. In a letter to Schiller he wrote

Everyone holds that the separation of hypothesis from fact is extremely difficult, but it is even more difficult than one usually thinks, because every presentation itself, every method, is already hypothetical. You as a third party… will better divide the hypothetical from the factual than I henceforth will be able to, because certain ways of conceiving things have indeed become inveterate with me and, as it were, facticized.

In any case, it does seem that Newton genuinely believed he was reporting proven facts, not advocating hypotheses. When the French Jesuit, Ignace Gaston Pardies, responded to Newton’s paper on colors with a comment on what he (Pardies) called Newton’s “hypothesis” of colors, Newton bristled at the word, and replied

I am content that the Reverend Father calls my theory an hypothesis if it has not yet been proved to his satisfaction. But my design was quite different, and it seems to contain nothing else than certain properties of light which, now discovered, I think are not difficult to prove, and which if I did not know to be true, I should prefer to reject as vain and empty speculation, than acknowledge them as my hypothesis.

Exchanges such as this not only prompted Newton to hone his rhetoric, they also caused him to be very cautious and circumspect about publishing speculative ideas as to the true nature of things – but of course he didn’t let this stop him from forming powerful conceptual models expressed in mathematical terms. Goethe too engaged in forming mental models, although he sought to gain a multiplicity of Vorstellungsarten rather than just one “true” model, and of course he was much less inclined to mathematize than was Newton. In fact, Goethe has the reputation for disdaining mathematics in general, an antipathy that has often been attributed at least in part to an awareness of his own lack of mathematical ability. He often wrote disparagingly about mathematics, as in the following famous epigram:

Mathematics has the completely false reputation of yielding infallible conclusions. Its infallibility is nothing but identity. Two times two is not four, but it is just two times two, and that is what we call four for short.  But four is nothing new at all. And thus it goes on and on in its conclusions, except that in the higher formulas the identity fades out of sight.

This criticism seems somewhat confused, because it begins by challenging the fallibility of mathematical conclusions, but then immediately replaces the charge of being fallible with the charge of be tautological. Now, tautologies actually are infallible, so the second sentence in that passage contradicts the first. Furthermore, the usual reason for regarding tautologies with disdain is that they are trivial (i.e., obvious, self-evident), but by admitting that, in the “higher formulas” of mathematics, “the identity fades out of sight”, Goethe is stipulating that the tautologies of mathematics are not trivial. Thus the quote does a respectable job of arguing that mathematics actually deserves its reputation of yielding infallible (and, by the way, non-trivial) conclusions, even though this is the opposite of what Goethe was (presumably) trying to say.

Goethe continued to develop his ideas about color, and his dislike of Newton, throughout the 1790’s, and eventually much of this was incorporated into his 1500 page book, Zur Farbenlehre (On the Theory of Colors), which he published in 1810. The first part of this book consists of an elaborate verbalization of Goethe’s “theory”, which is to say, his qualitative thoughts and observations of colors. These are presented as 920 numbered paragraphs, most consisting of just one or two sentences each, such as

155

If the darkness of infinite space is seen through atmospheric vapours illumined by the daylight, the blue colour appears.  On high mountains the sky appears by day intensely blue, owing to the few thin vapours that float before the endless dark space: as soon as we descend in the valleys, the blue becomes lighter; till at last, in certain regions, and in consequence of increasing vapours, it altogether changes to a very pale blue.

156

The mountains, in like manner, appear to us blue; for, as we see them at so great a distance that we no longer distinguish the local tints, and as no light reflected from their surface acts on our vision, they are equivalent to mere dark objects, which, owing to the interposed vapours, appear blue.

157

So we find the shadowed parts of nearer objects are blue when the air is charged with thin vapours.

158

The snow-mountains, on the other hand, at a great distance, still appear white, or approaching to a yellowish hue, because they act on our eyes as brightness seen through atmospheric vapour.

Toward the end of this part of the book, Goethe comments on the relationship of this subject to mathematics.

In the middle ages, mathematics was the chief organ by means of which men hoped to master the secrets of nature, and even now, mathematics in certain departments of physics is justly considered of paramount importance. The author can boast of no attainments of this kind, and on this account confines himself to departments of science which are independent of mathematics… The theory of colors… has suffered much, and its progress has been incalculably retarded by having been mixed up with optics, a science which cannot dispense with mathematics… The author of the present inquiry has endeavored throughout to keep the theory of colors distinct from the mathematics…

As an aside, it’s interesting that Goethe thought mathematics was predominant in physics during the “middle ages”, because historians of science today usually assert that the emphasis on mathematical thinking in physics began with Galileo and his contemporaries. In any case, Goethe then he goes further, and begins to reveal – for the first time in his published writings – the main object of his disapproval, although at this point he still doesn’t explicitly name the culprit.

Besides this, there was an additional evil. A great mathematician was possessed with an entirely false notion on the physical origin of colors; yet, owing to his great authority as a mathematician, the mistakes which he committed as an experimentalist long became sanctioned in the eyes of a world forever fettered in prejudices.  [We will] return to this point hereafter, on an occasion where it will be necessary to speak with less reserve.

The relatively subtle and understated approach he had taken in Beitrage zur Optik (which he mostly continued in the first part of Zur Farbenlehre) had not been successful in dislodging the false “Newtonian teaching”, so in the later section of Zur Farbenlehre Goethe decided to sharpen his attack and “speak with less reserve”. He wrote a lengthy and often vitriolic polemic against Newton and all the misguided physicists who have made careers out of repeating and defending Newton’s errors. Not surprisingly, it was not well-received by physicists. (Thomas Young, founder of the wave theory of light, said Zur Farbenlehre was “a striking example of the perversion of the human faculties”.)

It’s hard to imagine that no one ever explained to Goethe why the white wall still appeared white when viewed through the prism, and why it was perfectly consistent with Newton’s conception of differential refrangibility. The explanation can basically be read directly off of Newton’s 1665 drawing, or by simply reversing the directions in the basic projection schematic, as shown below.

According to Newton, every ray of light emanating from the white wall consists of a mixture of all the spectral colors, but only the red component of the upper ray is refracted into the ray entering Goethe’s eye, and only the violet component of the lower ray is refracted into that ray. (The other components of the upper and lower rays are refracted at different angles, and hence do not emerge from the prism along that particular ray leading to the eye.) In effect, the final ray of white light entering Goethe’s eye is composed of all the spectral colors gathered from different points on the wall. It might seem miraculous that it should work out this way – until we realize that it’s just the reversal of the original experiment, the one that projected the spectrum of colors onto the wall.

Of course, this also explains (in Newtonian terms) why Goethe saw colors near boundaries. If, for example, we darken the part of the wall where the violet and blue components originate, then the ray entering the eye will no longer be white. Indeed, we could make the wall appear red by darkening or blocking all except the rays coming from the wall at the angle that refracts red light through the prism. (This is reminiscent of diffraction gratings.)

So, not only does Newtonian theory account for Goethe’s observations, it immediately suggests new phenomena, and ways of manipulating the elements of the experiment to produce specified results. This interesting explanation, although perhaps not intuitively obvious (as it obviously wasn’t to Goethe), follows mathematically from Newton’s conception of light and differential refrangibility. It’s tempting to say that Goethe’s observation is tautological from Newton’s premises, and yet Goethe interpreted the observation as a self-evident disproof of those premises. (Does it require a mathematical mind to grasp the reverse phenomenon?) Surely, one thinks, someone must have explained it to him. And yet, to the end of Goethe’s long life, there is no evidence that he ever heard or understood this explanation, nor that he ever changed his mind about how a single glance through a prism had been sufficient to prove that “Newtonian teaching is false”.

Goethe’s greatest achievement is usually considered to be his re-shaping of the Faust legend in the form of a great epic poem. (Interestingly, like Faust, both Newton and Goethe were at one time students of alchemy, and Newton in particular has been called the last of the Magi, which places him squarely in the Faustian tradition – although this aspect of Newton’s life was not well known in the 18th century.) At the conclusion of Part II, which Goethe completed just months before his death, Faust attains salvation through the pursuit of knowledge and truth. This theme of redemption was evidently adapted from fragments of a projected Faust play by Gotthold Lessing, published posthumously in 1784. (Lessing was often credited by the physicist Albert Einstein for the fine saying that “The search for truth is more precious than its possession”.) Goethe incorporated his vast knowledge of many different fields, including science, into his Faust. In the first act of Part II he appeals to images of light and color to convey what he sees as the essential pluralism of life, urging us to resist the (Newtonian?) tendency to narrow ourselves down to one single way of thinking about things.

The rainbow mirrors human aims and action.

Think, and more clearly wilt thou grasp it, seeing

Life is but light in many-hued reflection.

One of Goethe’s main motivations in his Farbenlehre was a desire to assert the inviolability of the colors of experience, including white light, and to reject any analysis or mechanization of these primitive experiences. It is sometimes said that Goethe’s ideas were more consonant with studies of how light and colors are perceived, as opposed to the physics of light as an objective phenomenon, but it isn’t clear that Goethe could have accepted (for example) the subsequent understanding of color perception in terms of just three types of color receptors in the human eye. This actually provides an even more mechanistic and analytical view of colors, since not only is it based on what Goethe regarded as the “reductionist “ frequency interpretation of light, it goes even further by reducing the sensory input to just three distinct types of stimuli (i.e., three different frequency ranges). It seems unlikely that Goethe could ever have embraced these ideas.

One of Goethe’s main objections to Newton’s work on colors was that Newton conflated his own conceptual interpretations of events with the actual experiences. Indeed, even by referring to “rays” of light, Newton was imposing a conceptual framework onto the subject, and thereby (as Goethe would say) prejudicing the interpretation of the raw experiences. We can always imagine different ways of conceptualizing our sensations, and Goethe thought Newton was, at best, insufficiently imaginative to recognize these alternative conceptual frameworks, or, at worst, cynically trying to suppress every interpretation other than the one he had capriciously selected with no apparent justification. In this respect, Goethe failed to appreciate the extent to which a great scientist like Newton is actually a great artist. He does indeed make choices, and the reasons for those choices may not be clearly articulated. They may be motivated by some intuitive sense for what conceptual framework is most capable, in the present state of knowledge, of capturing and representing the phenomena. This is a profoundly creative act, something that Goethe seems not to have appreciated. In the concluding comments of Zur Farbenlehre, Goethe remarked on what he regarded as an important difference between art and science:

When we consider art in its higher character, we might wish that only masters had to do with it … that amateurs might feel themselves happy just to reverentially approach its precincts. For a work of art should be the effusion of genius, the artist should evoke its substance and form from his inmost being, treat his materials with sovereign command, and make use of external influences only to accomplish his powers. But … the man of science has every motive to be more indulgent, since the amateur here is capable of contributing what may be satisfactory and useful. The sciences depend much more on experiment than art...

It could be argued that this paragraph would be more apt if the words “art” and “science” were everywhere transposed. Ironically, Goethe seems to have grasped, on some level, the necessity for a great scientist to deploy the full range of intellectual and spiritual resources, although he imagined that this necessity had never before been recognized, let alone fulfilled. He wrote

Just as art always presents itself as complete in every single artwork, so should science always show itself whole in every single thing it treats. But to come close to meeting such a demand we must not exclude any of the human powers from scientific activity. The abysses of intuition, a sure view of the present, mathematical depth, physical precision, sublimity of reason, sharpness of intellect, agile, yearning fantasy, loving joy in the sensuous: Nothing can be foregone if there is to be a lively, fruitful seizing of the moment, through which alone a work of art, whatever its content may be, can arise. Even if these required elements may seem to be, where not contradictory, yet nonetheless opposed to one another in such a way that even the most excellent spirits could not hope to unite them: They nevertheless still reside manifestly in the whole of humanity and can emerge at any moment...

Here Goethe was expressing a conception that might be called the heterogeneity of life. The wholeness of humanity (white light) contains implicitly within it the different “colors” of intuition, reason, fantasy, sensuality. So, for one last irony, it appears as if the Newtonian concept of heterogeneous white light being composed of all the colors of the rainbow – the concept that Goethe had despised and combated for so many years – came to be the metaphor for his own sublime conception of art, science, and life. When Goethe died in 1832 at the age of 82, his last words were “More light!”

Return to MathPages Main Menu