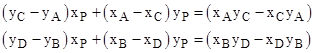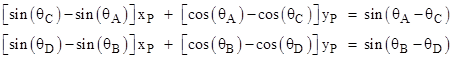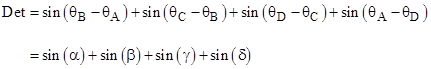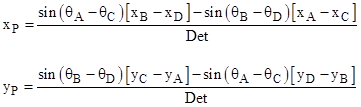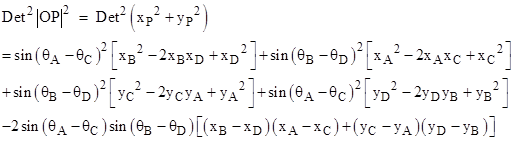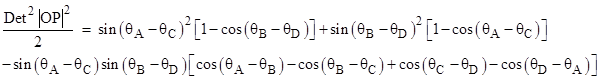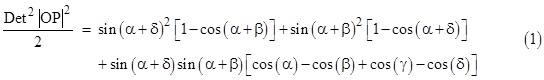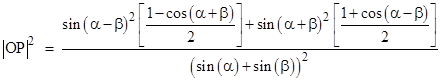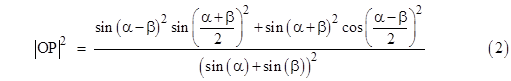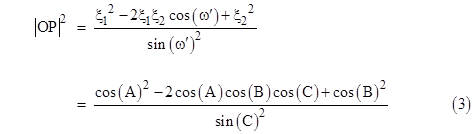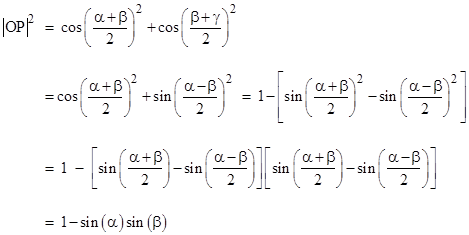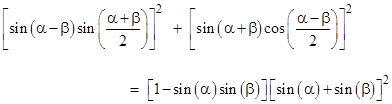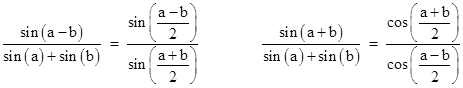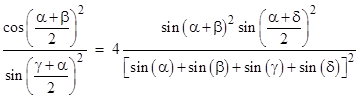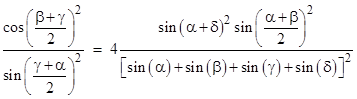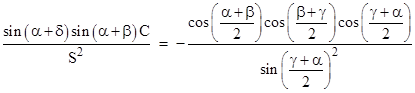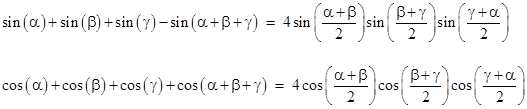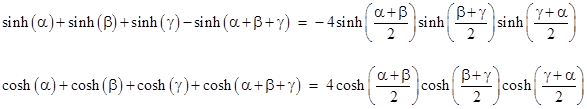Cyclic Quadrilaterals Revisited

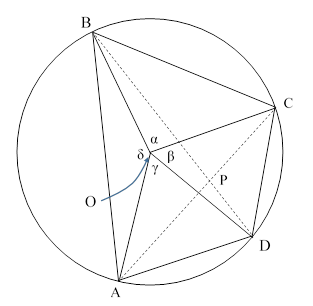
Consider a quadrilateral ABCD inscribed in a unit circle, as shown below.

The point O is the center of the circle, and the point P is the intersection of the diagonals. As discussed in another note, in terms of a system of Cartesian coordinates x,y with origin at O, the coordinates of P are related to the coordinates of A, B, C, and D by the two equations

Thus we have

Letting θ_A denote the (counter-clockwise) angle between the positive x axis and the radial segment OA, and similarly for the other angles, this system of equations can be written as

The determinant is

and the coordinates of the intersection point P are

The squared distance from the origin to the point P satisfies

Consolidating terms and re-arranging, this reduces to

Replacing the differences with the sums of the central angles, this can be written as

Naturally we can eliminate one of the central angles using the relation α + β + γ + δ = 2π.

We note that the diagonals are perpendicular just if a + c = π/2, which is true if and only if α + γ = π, which is equivalent to the condition β + δ = π. In this special case we can eliminate two of the angles, say, γ and δ, and write the distance equation as

This can also be written as

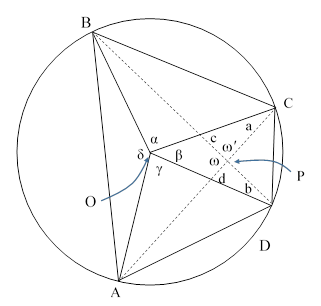
For a more direct solution, leading to more succinct expressions, consider the general quadrilateral shown below with the angles a,b,c,d surrounding the diagonal intersection point as marked.

We have the following relations

and also π – c = π – (β+b), from which we have c = β + b. We can regard the dashed diagonals as the axes of an oblique coordinate system at an angle ω′ given by

The perpendicular distances from the diagonals to the origin O are

Using the line element for an oblique coordinate system as shown in Figure 3 of the note on “Tensors, Contravariant and Covariant”, we have

where

Recalling that the diagonals are perpendicular just if α + γ = π, we see immediately that the distance |OP| in the orthogonal case satisfies

Equating this to the previous expression (2) gives the interesting trigonometric factorization of a sum of squares into three linear factors

This can be derived algebraically from (2) making use of the identities

The individual terms of equations (1) and (3) correspond to each other, so we have

and both of these reduce to

The remaining corresponding terms of (1) and (3) are

where C is the sum of the cosines with alternating signs, and S is the sum of the sines. From this we get

We can eliminate δ from these equations, and replace β with β+π in the cosines, and arrive at the interesting identities

Recall from the note on a quarky volume formula that the volume of a parallelapiped can be expressed simply using the products of three sines of the angles between the edges and between the faces. It can be shown that similar identities (except for one sign) apply to the hyperbolic functions

We also have the identity

The independence of the left side from the value of b can be verified by noting that the derivative with respect to b vanishes.

Return to MathPages Main Menu