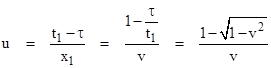Slow Clock Transport

Einstein’s 1905 paper on special relativity describes a method of synchronizing clocks based on the proposition that the speed of light is isotropic (the same in all directions). The method he described was equivalent to flashing a light bulb at the midpoint of a rod, and assigning the same time coordinate to the arrivals of the pulses at the ends of the rod, so those events are simultaneous in terms of these coordinates in which the rod is at rest. In later writings (see, for example, his 1910 “The Principle of Relativity and its Consequences in Modern Physics”), Einstein noted that we can equally well use any other kind of isotropic signal, such as sound waves that propagate through a medium that is at rest with respect to the end points. Most simply of all, we can place two identical material particles at rest at the midpoint of the rod and let them repel each other, and assign the same time coordinates to their arrivals at the end points of the rod. The latter is basically the definition of simultaneity for an inertial coordinate system, i.e., a system in terms of which mechanical inertia is homogeneous and isotropic (meaning the inertia of an object is independent of location, time, or orientation). The essential empirical content of special relativity derives from the fact that these methods yield the same simultaneity.

Einstein did not explicitly state this obvious fact in his 1905 paper, but it’s clearly implicit, as in the very first sentence of Section 1, where he says “Let us take a system of coordinates in which the equations of Newtonian mechanics hold good (to the first approximation)”. Note that he defines this class of coordinates, which we will call inertial coordinates, not just by Newton’s first law, but by all of Newton’s laws, which signifies that, as above, identical particles repelling each other from rest will reach equal distances in equal times. This was not a novel idea… Galileo himself stated that if we jump with equal force in any direction we will reach equal distances in equal times. The fundamental symmetries of homogeneity and isotropy are, and always have been, the defining attributes of inertial coordinate systems. Thus the full definition of “inertial coordinate system” entails a definite simultaneity that can be established by purely mechanical means. Also, the proposition that, for any material particle, there exists such a coordinate system in which the particle is instantaneously at rest expresses what’s needed from the principle of relativity to derive the relationship between such systems.

Unfortunately, Einstein didn’t emphasize the inertial definition of simultaneity in his original 1905 paper, and a mistranslation in the English reprint made matters worse. Perrett and Jeffery translated a key passage as

We have so far defined only an A-time and a B-time. We have not defined a common time for A and B, for the latter cannot be defined at all unless we establish by definition that the time required by light to travel from A to B equals the time it requires to travel from B to A.

A correct translation (as found in Einstein’s Collected papers, for example) has this passage as

Thus far we have only defined an A-time and a B-time but not a time common to A and B. The latter can now be determined by establishing by definition that the time needed for the light to travel from A to B is equal to the time it needs to travel from B to A.

The mistranslation claims that simultaneity can be established only by defining the speed of light to be isotropic (which is absurd), whereas the correct translation merely says we can establish a common time coordinate with this definition. However, even with the correct translation, Einstein’s statement is still somewhat misleading, because he actually defined a common time coordinate for A and B previously, by stipulating at the very beginning “a system of coordinates in which the equations of mechanics hold good in the first approximation”. As explained above, this suffices to establish the time coordinate and distant simultaneity. Part of the difficulty is that Einstein was still often using the term “coordinate system” to refer only to the spatial coordinates, referring to time as a separate parameter, but the stipulation that all the equations of Newtonian mechanics hold good (in the low speed limit) implicates the time coordinate as well, and fixes the unique temporal foliation that (as he later explicitly recognized) yields isotropic mechanical inertia.

The lack of clarity in the early expositions led to decades of pointless and misguided debate about whether simultaneity is conventional and/or merely a matter of arbitrary definition, and so on. Also, the fact that Einstein’s 1905 paper (with or without the mistranslation) placed so much emphasis on the use of light signals has led to the mistaken idea that the invariance of the speed of light in terms of inertial coordinates is circular. There are professional physicists even today who deny that inertial synchronization of time can be established purely by mechanical means based directly on the definition of inertial coordinates. The decision to express things in terms of inertial coordinate systems is, of course, a free choice, i.e., a convention (although far from an arbitrary one), but there is no ambiguity as to the temporal foliations of inertial coordinate systems.

For example, it is meaningless to say “the speed of light is always c”, but it is both meaningful and empirically true that “the speed of light is c in terms of any system of inertial coordinates”, with the understanding that inertial coordinates are defined not just by the requirement to be unaccelerated, but by the requirement for mechanical inertia to be homogeneous and isotropic in terms of those coordinates.

Another contributor to the confusion is the two different definitions of inertial coordinate systems, the incomplete one based purely on the requirement to be unaccelerated (Newton’s first law), and the complete one that also requires inertia to be isotropic so we have equal action and reaction. As a remnant of pre-relativistic days, many people think inertial coordinate systems are completely defined by the requirement to be in free fall (unaccelerated), meaning that Newton’s first law is satisfied, but then they immediately assert that the others equations of mechanics (in homogeneous and isotropic form) are satisfied in terms of those coordinates, which is not generally true. If we start with an inertial coordinate system, i.e., a system in which all of the equations of Newtonian mechanics are satisfied (in the low speed limit), and tilt the temporal foliation, then in terms of these new coordinates the spatial points are still in free-fall (unaccelerated) and the trajectories of free objects are all still linear (“first law”), but the equations of Newtonian mechanics are no longer satisfied.  So there are certainly coordinate systems for which the spatial points are in free-fall, but in terms of which inertia is not isotropic.

Of course, nothing requires us to use inertial coordinate systems, with either the full definition or the partial definition. There are infinitely many other coordinate systems with other synchronizations, but inertial coordinate systems (full definition) are particularly useful, because, as Copernicus and Newton discovered, physical phenomena take a particularly simple form when expressed in terms of such coordinates. Special relativity asserts that the speed of light is c in terms of any such system of coordinates, which is not a circular assertion.

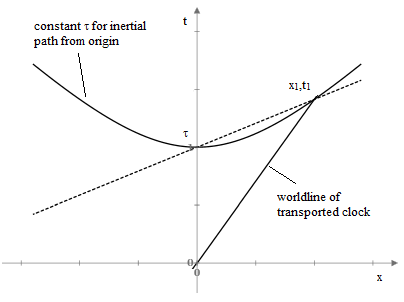
One technique that is sometimes mentioned for synchronizing distant clocks is known as “slow clock transport”. This is actually a derived result (ultimately based on the invariance of physical laws in terms of inertial coordinates) for what can be called ideal clocks, which are defined as devices that indicate elapsed proper time. Synchronization by slow clock transport is more complicated than some might think, and problematic for foundational purposes. The figure below shows a simple diagram of the world line of a clock transported from the origin to the event x₁,t₁ at some speed v = x₁/t₁.

The Minkowski line element in terms of inertial coordinates x,t is

so in our situation we have τ² = t₁² – x₁² (using units so c=1 for convenience). From the slope of the time axis, we see that the inertial coordinates in terms of which the transported clock at x1,t1 and the “stationary” clock at 0,τ are simultaneous (both reading τ) is the system moving to the right at the speed u given by

For small v this is approximately v/2. Hence, the stationary and transported clocks are not synchronized in terms of the stationary coordinates, but rather in terms of a coordinate system moving with about half the speed of the transported clock. To distinguish between the inertial coordinate systems with mutual speed V, it is necessary for the clock transport speed to be small, not just in comparison with c, but in comparison with V. Thus clock transport as an operational process is inherently approximate, and can only approach exactness as the clock transport speed approaches zero, corresponding to infinite transport time for any non-zero distance.

Moreover, slow clock transport relies on treating the high-level and somewhat ambiguous concept of a “clock” as a primitive element, which is already unsatisfactory. As Einstein noted, “measuring rods and clocks should emerge as solutions of the basic equations, not, as it were, as theoretical self-sufficient entities”. A variety of things can be called “clocks”, such as sun dials, etc., so at the very least we need to invoke an “ideal clock”, but the definition of an ideal clock is essentially one that indicates proper time, based on the principle of relativity, i.e., for any state of motion of a material particle there is a system of coordinates in terms of which the particle is at rest and the equations of physics take their standard (homogeneous and isotropic form). A practical embodiment of an ideal clock is not trivial. If we use “light clocks” to measure the speed of light we can be suspected of circular reasoning. If we use atomic clocks we are invoking the probabilistic decay times for hyperfine transitions between quantum energy levels – on which the effect of relative motion is hardly self-evident. Ultimately, the only cogent applicability is for processes based on mechanical inertia itself (e.g., mass-spring systems), but then we don’t even need the high-level “clock”, we just invoke the primitive isotropy and homogeneity of inertia, which is after all the defining attribute of the subject coordinate systems.

Historically, Eddington invoked slow clock transport in his “The Mathematical Theory of Relativity” (1923), and he actually used it as a primitive postulate in his derivation (or rather, plausibility argument) for the Minkowski metric. He begins by suggesting (somewhat vaguely) that the metric ought to be quadratic, and since time is different from space, the coefficient of time should be fundamentally different from space, so he proposes to assume that time and space are mutually “imaginary” (i.e., the units are related by an imaginary factor), and hence he says the general quadratic line element would be of the form

(I’ve converted his spacelike interval to a timelike interval, and simplified a bit.) He then uses slow clock transport to “prove” that α must equal zero. It should be noted that if we make the coordinate substitution t′=t+kx, x′=√(1-k²) into the standard line element (1) for inertial coordinates we get

which is perfectly valid and physically equivalent to the standard line element, merely expressed in terms of different coordinates. Note that, in terms of these coordinates the equations of mechanics are not isotropic, because the locus of simultaneity is skewed relative to inertial simultaneity. This doesn’t prove that α in (2) must equal zero, it simply shows that α equals zero if and only if x,t is a system of inertial coordinates (which we already know from the definition of inertial coordinates, although Eddington apparently didn’t realize this).

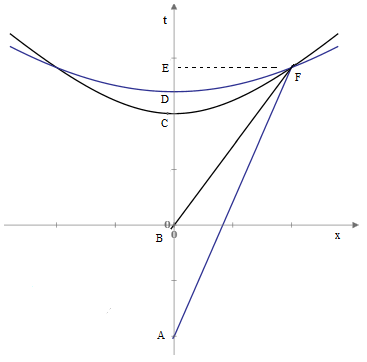
Obviously a choice of coordinates doesn’t affect the behavior of clocks. Eddington’s premise (although he doesn’t express it this way) is really that we should choose coordinates such that for any locus of constant τ for inertial world lines from the origin we have dt/dx = 0 at x=0. In other words, the hyperbola of constant τ must be tangent to the space axis of our coordinates at x=0. This is necessary and sufficient to ensure that, for a range of sufficiently small transport speeds, the locus of simultaneity for proper time approaches alignment with the locus of simultaneity for coordinate time. Note that the difference between the elapsed proper times and coordinate times goes to zero at x=0, even if the axes are skewed, so this is not a sufficient condition. We require that the slopes approach alignment, in order for the coordinates in which the clocks are exactly simultaneous to approach the “stationary” coordinates. The figure below illustrates this requirement.

The hyperbola through C represents the locus of events with the same elapsed proper times from event B for inertial world lines emanating from B. Likewise the hyperbola through D represents the locus of events with the same elapsed proper times from event A for inertial world lines emanating from A. An ideal clock transported from B to F will differ from the coordinate time at F by the amount t_E – t_C, whereas an ideal clock transported from A to F (hence at a lower speed than the previous clock) will differ from the coordinate time at F only by the lesser amount t_E – t_D. Pushing the starting point for the transport further and further into the past, resulting in slower and slower transport speed, the amount by which the reading on the clock at F differs from the coordinate time can be made arbitrarily small as the hyperbola becomes flatter and flatter.

But if we superimpose the x′,t′ coordinates defined above, the x′ axis is tilted relative to the asymptotically flat hyperbola, so the proper time will always differ from the coordinate time by the amount proportional to the spatial distance due to the tilt of the axis. This tilt of the x′ axis corresponds to using the non-standard simultaneity, i.e., a simultaneity different from that which is based on isotropy of inertia. In other words, x′,t′ is not an inertial coordinate system, as shown by the fact that two identical particles initially at rest at the origin and repelling each other would not have equal magnitudes of dx′/dt′. Thus, slow clock transport is superfluous, as well as being epistemologically problematic.

Eddington himself seems to have been unsure if slow clock transport was really a valid fundamental premise:

I do not know how far the reader will be prepared to accept the condition that it must be possible to correlate the times at different places by moving a clock from one to the other with infinitesimal velocity.

To his credit, he recognized (to some degree) that neither of the two statements

(1) A clock moved with infinitesimal velocity from one place to another continues to read

      the correct time.

(2) The forward velocity of light along any line is equal to the backward velocity.

has empirical meaning. However, his appraisal of the situation is expressed in a somewhat problematic way. He writes

Neither statement is by itself a statement of observable fact, nor does it refer to any intrinsic property of clocks or light; it is simply an announcement of the rule by which we propose to extend fictitious time-partitions through the world.  But the mutual agreement of the two statements is a fact which could be tested by observation…

What he ought to say is that the two statements are simply meaningless without defining the word “correct” in the first and “velocity” in the second, but if we stipulate that these words refer to any system of coordinates in terms of which the equations of physics take their standard form (i.e., inertia is homogeneous and isotropic), then both of those statements are empirically true. The early focus on conventionalism was a red herring, although perhaps useful to emphasize the necessity of giving operational meanings to our statements. As Einstein later remarked

With the given physical interpretation of coordinates and time [still not referring to time as a coordinate, even in 1949], this is by no means merely a conventional step but implies certain hypotheses concerning the actual behavior of moving measuring rods and clocks, which can be experimentally confirmed or disproved.

Again, it’s meaningless to say “the speed of light is always c”, without specifying a system of coordinates, but it is an empirical fact that the speed of light (in vacuum) is c in terms of every system of inertial space-time coordinates, and this is not a trivially circular statement, because such coordinates are fully defined by the isotropy and homogeneity of mechanical inertia, not by the isotropy of light speed. Admittedly, the fact that all forms of energy (mechanical, electromagnetic, etc.) have inertia is an underlying common cause, but this universality ensures that relativity and Lorentz invariance encompass all phenomena, which doesn’t make them circular – although to a sufficiently elevated awareness one might argue that it makes them tautological (within any sufficiently coherent context), which is hardly objectionable.

Perhaps influenced by early writers like Eddington, who presented just two alternative means of establishing the inertial synchronization of separate clocks – neither of which simply employs the defining characteristic (i.e., isotropic inertia), may later writers seem to have assumed that these were the only two methods, and ignored not only the problematic aspects of slow clock transport but also the most simple and fundamental method. For example, Taylor and Wheeler give only those two methods, and even Ohanian’s criticism of “Einstein’s mistake” just invokes slow clock transport as the alternative to isotropic light speed, overlooking that Einstein himself later clearly explained the general method based on any isotropic signal for which “we have no reason whatsoever to think the phenomena of signal transmission would differ in opposite directions”. Einstein explicitly noted that, for example, striking a uniform solid rod at the midpoint would result in sound waves reaching the ends simultaneously in the rest frame of the rod. Likewise Wald notes that

An inertial observer can have a clock placed at each grid point and can synchronize each clock with his by a symmetrical procedure, e.g., by making sure that a given clock and his give the same reading when they receive a signal sent out in a symmetrical manner by an observer stationed halfway between the two.

Thus he does not make the mistake of thinking the signal must be light pulses, although he doesn’t quite explain that the defining attributes of an inertial coordinate system (with the full definition) already entails a specific operational definition of simultaneity.

To be clear, the “isotropy of mechanical inertia” means that (for example) if two identical material particles, released from rest at the midpoint of a rod, repel each other, they will reach the ends of the rod simultaneously in terms of space-time coordinates in which the rod is at rest and in which the equations of Newtonian mechanics hold good in the low speed limit (the latter condition being the definition of an inertial coordinate system). Of course, this just establishes inertial coordinates (including temporal synchronization) intrinsically for any state of motion, it doesn’t imply how such systems are related to each other. However, if we perform this same procedure for a rod in motion in terms of a given system of inertial coordinates, we find that the resistance to acceleration (inertia) of the forward-going particle is greater than the rearward-going particle, in proportion to the difference in their kinetic energies in this frame, so they do not reach the ends simultaneously in terms of these inertial coordinates, even though they do in terms of the inertial coordinates in which the rod is at rest. Hence simultaneity is relative and the inertia of a body depends on its energy content. The Lorentz transformation and all of special relativity follow from this. This is why, regarding the relation between inertial mass and rest mass, Feynman wrote that, for purposes of solving problems (i.e., the empirical content of the theory), “That is all there is to the theory of relativity – it just changes Newton’s law by introducing a correction factor to the mass”.

Indeed, given the existence of inertial coordinate systems, by the very definition of such systems the transformation between any two of them must map straight world-lines to straight world-lines (and finite to finite), so it must be linear, and then by isotropy (which implies reciprocity) simple algebra suffices to show that the transformation must be of the form T=(t–kvx)γ, X=(x–vt)γ where γ = 1/√(1–kv²) for some constant k. Now, let u and U be the speeds of a particle in inertial coordinates x,t and X,T, respectively. We have u=(v+U)/(1+kvU), and hence du/dU=(1–kv²)/(1–kvU)², so when the particle is momentarily at rest in X,T we have du=(1–kv²)dU. Also, at U=0 (meaning dX=0) the transformation gives dT=dt √(1–kv²) so we have du/dt = (1–kv²)^3/2 dU/dT.  Now, as the particle is instantaneously at rest in X,T, the instantaneous acceleration is dU/dT= F/M where M is the rest mass. By symmetry, the force (parallel to the motion) in terms of x,t is the same as in X,T (see below), but the acceleration is du/dt, so we have F = [M/(1–kv²)^3/2] du/dt.  The quantity in square brackets is what used to be called the “longitudinal mass”. Noting that du/dt=dv/dt at constant U=0, we have F=dp/dt where p=v[M/√(1–kv²)] and the quantity in square brackets is called the inertial (or relativistic) mass. This if we know that the inertial mass of a particle is M√(1 – v²/c²), we know that k=1/c², and hence inertial coordinate systems are related by Lorentz transformations. (If k was equal to zero, they would be related by Galilean transformations, and if k was negative they would be related by Euclidean transformations.)

Regarding the transformation of force, note that the force in this scenario is parallel to the motion, for which, by symmetry, the force exerted by A on B in the rest frame of A equals the force of B on A in the rest frame of B.  Naturally this is consistent with the transformation of 3-force under Lorentz transformations, but we do not need to invoke the Lorentz transformation of forces to assert this symmetry; it is implied by isotropy and the existence of inertial coordinate systems.

On a related point, people are sometimes confused by Einstein’s comment that the general theory of relativity showed that the law of invariance of the speed of light does not have unlimited validity. In the context of general relativity we know that global systems of inertial coordinates do not exist (because of intrinsic curvature), and hence in every global system of coordinates the speed of light is variable. Einstein wasn't denying that we can still define, around any event, local inertial coordinates in which the speed of light is c, he was pointing out that we can't define a global system of coordinates in which light speed is invariant, and this has physical consequences, such as deflection of light rays.

For example, in a spherically symmetrical gravitational field, the most convenient systems of coordinates (e.g., Schwarzschild or isotropic) use the essentially unique time coordinate t for which the metric coefficients are independent of t, and the speed of light varies from place to place.  Sure, we could use local free-fall coordinates in any particular region, in terms of which the speed of light is c, but those are limited to a small time and place, and they tend to crash into the gravitating mass very quickly. So we almost always use stationary coordinates (when possible), and in terms of such coordinates the speed of light varies from place to place, and rays of light are curved, etc. (In Schwarzschild coordinates the speed also depends on the direction of the ray.)

Oddly enough, while acknowledging that the speed of light can have any value we choose in terms of a suitable system of coordinates (as Einstein said, “it is not so easy to free one’s self from the idea that coordinates must have direct metrical significance”), they maintain that any such coordinates are somehow “perverse”, and do not represent “physical reality”. Needless to say (or so one would have thought), that is absurd. For example, Schwarzschild coordinates are not "perverse".  They have a very clear operational definition, and they (or the related isotropic coordinates) are actually used quite commonly, and for good reason. In most practical situations we use a "global" stationary coordinate system, not a local free-falling transitory coordinate system. This doesn’t mean the speeds in terms of the global coordinates are "not physical reality". Yes, local free-falling inertial coordinates (Riemann normal) are physically distinguished, but so are coordinates in which time is a Killing vector (e.g., Schwarzschild coordinates). Yes, local free-fall coordinates are important for understanding the equivalence principle, but this doesn’t make them uniquely "true" or "physically real". The physical reality is independent of coordinates, but speed just happens to be a coordinate-dependent quantity.

In summary, relativity does not assert the speed of light is c in terms of every system of coordinates, it asserts that the speed of light is c in terms of every system of inertial coordinates, defined as coordinates in which all the equations of Newtonian mechanics (not just the first law) hold good in the low speed limit. These coordinate systems are defined without reference to the behavior of light, so the assertion is not circular. Naturally in terms of accelerating coordinates and/or global coordinates in the presence of gravitating bodies, the speed of light need not be – and generally is not – equal to c, but it is always c in terms of the local free-falling inertial coordinates.

Return to MathPages Main Menu