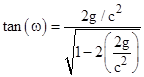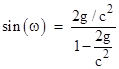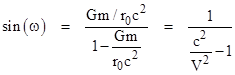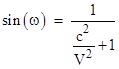Soldner’s Deflections

All nature consists of bodies and of void

In which they're set, and where they're moved around.

There's naught of which thou canst declare

It lives disjoined from body, shut from void -

A kind of third in nature.

                Lucretius, De Rerum Natura, I, 420

Isaac Newton explained how to determine the trajectory of a particle moving in a central gravitational field, showing that the path is a conic section, i.e., an ellipse, parabola, or hyperbola, depending on the initial conditions. A simple example of this is for a particle moving relative to a gravitating body of mass m in a hyperbolic path at a certain high speed v, which could be specified as the particle’s asymptotic speed far from the gravitating body, or its speed at the point of closest approach. Using Newton’s method it is straightforward to show that, in either case, the angle ω between the direction at closest approach at distance r₀ and the asymptotic out-going (or in-coming) direction is, to the first order, ω = Gm/(v²r₀), and hence (according to Newton) the total deflection angle between the in-coming and out-going asymptotes of the path is 2ω = 2Gm/(v²r₀) as shown below.

Historically, an unpublished (and undated) comment of Henry Cavendish, possibly written as early as 1784 (prompted by the letter John Michell sent to him in 1783 on the idea that light might not be able to escape from a sufficiently massive body, if light behaved like particles), noted that if we naively regard light as tiny material particles moving at the speed c (at infinite distance), then Newton’s laws imply, to the first order, that light would be deflected by ω = Gm/(c²r₀) radians from one asymptote to the tangent point. When viewing stars near the edge of the Sun during a total eclipse, this implies that the rays reaching the Earth would be deflected by about 2ω = 0.875 arc seconds. (Cavendish’s note actually said that if V denotes the speed of a circular orbit at radius r₀, then the sine of the half deflection angle ω equals 1/[1+(c/V)²], which to the first order is equivalent to the given expression, noting that V²/r₀ = m/r₀² for a circular orbit.)

Around 1801 a self-taught astronomer’s assistant named Johann Georg von Soldner – whose only formal schooling was two years of grammar school as a boy – performed the same fairly trivial exercise in elementary Newtonian mechanics, perhaps at the urging of Johann Bode, to determine whether the effect was large enough to be appreciable in astronomical observations on Earth, and this was published in 1804. The paper drew little attention at the time, although a century later it received some notoriety when it was re-published by Philipp Lenard in 1921 for the purpose of comparing it with Einstein’s prediction of light deflection in general relativity. Unfortunately, Soldner’s paper contains several peculiarities that need to be carefully taken into account in order to understand what he actually said.

First, Soldner frequently speaks in terms of “decimal seconds” (an innovation in the spirit of the French Revolution), by which the day consisted of 10 decimal hours, each of which consisted of 100 decimal minutes, each consisting of 100 decimal seconds, so there were (10)(100)(100) = 100,000 decimal seconds in a day, whereas there are (24)(60)(60) = 86,400 seconds in a day. Hence each decimal second is 0.864 seconds.

Next, it was conventional in the German technical literature at that time to use the symbol “g” to refer to the distance an object would fall from rest in one unit of time, which is half of the acceleration of gravity. Recall that Galileo had discovered that the distance, s, an object falls from rest is proportional to the square of the time, t, and some people expressed this as s = gt² where the constant of proportionality “g” was called the acceleration of gravity. Of course, in modern terminology, the actual acceleration is defined by the linear relation v = gt, which is integrated to give s = (1/2)gt². So, what Soldner called “g” is what we call g/2. This is confirmed by the numerical value that Soldner quotes for g at the Earth’s surface, which he gives as “3.66394 meters”, tacitly per decimal second squared, which is 4.90818 meters per second squared, thus exactly half of 9.816 meters/sec².

A third source of potential confusion is that Soldner chose to use a different unit of distance for each problem, equal to the radius of whatever astronomical body he was discussing. He did this ostensibly to “simplify” the expressions, but it obscures both the dependence of the deflection angle on the distance of closest approach and the dimensional relations. For example, in his ad hoc units of distance, he says the radial acceleration of a unit mass at a distance r from the center of attraction is 2g/r², but what he calls “r” is really the dimensionless ratio r/r₀ in arbitrary units, in which case g has the consistent units of acceleration on both sides of the equation, i.e., distance/time².

Now, with all these things in mind, we can review Soldner’s actual expressions. By an unnecessarily lengthy and elaborate sequence of steps, in which he refers to Laplace for some trivial facts (perhaps a drawback of being a self-taught calculator), Soldner finally arrives at his result, which he expresses as

By a simple trigonometric identity this is equivalent to

Accounting for the fact that Soldner’s g is actually g/2 where g is what we call the acceleration of gravity, his quantity 2g/c² in modern terminology is g/c², which has units of distance⁻¹, so to make it a dimensionless angle (radians) we must multiply by Soldner’s ad hoc distance unit, which is r₀. Hence in modern terminology and arbitrary units Soldner’s expression 2g/c² is actually gr₀/c². The acceleration of gravity per unit mass at the surface of a body of mass m and radius r₀ is g = Gm/r₀², so Soldner’s result in ordinary units is

where V is (again) the speed of a circular orbit at radius r₀. We see that this differs from Cavendish’s result

only by the sign in the denominator, due to the fact that Cavendish takes the speed of the light particle to be c at infinity (and therefore slightly greater than c at perigee), whereas Soldner takes the speed of the light particle to be c at the perigee (and therefore slightly less at infinity). These expressions also agree with the results for both cases in Bending Light. Since c²/V² is many orders of magnitude greater than 1, and since the angle ω is so small, both cases are essentially just ω = (V/c)², which is to say that, according to Newtonian physics, the half-deflection is ω = Gm/(c²r₀), and for the full deflection (between in-coming to out-going asymptotes) is 2ω = 2Gm/(c²r₀). We should emphasize that there is nothing new here. Newton in 1687 has already explained how to determine the hyperbolic trajectories of particles passing a spherical gravitating body, and of course he had noted the possibility that light follows trajectories like material particles. Neither Cavendish in 1784 nor Soldner in 1801 was adding anything new.

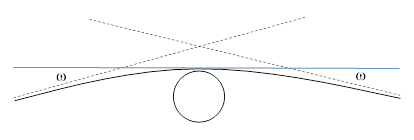
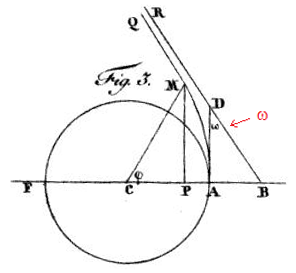
Soldner’s drawing, indicating the half-deflection ω, is shown below. We note that Soldner speaks interchangeably of light moving from A to Q or from Q to A, since the branches are symmetrical.

For his numerical results, he first considered the deflection of light due to the Earth’s own gravitational field, by viewing light from the horizon, i.e., for rays tangent to the Earth’s surface. One further erratum in Soldner’s paper is that he somehow used an erroneous value for the speed of light in this calculation. He says light requires 564.8 decimal seconds to go from Sun to earth, which implies a speed of about (3.07)10⁸ meters/sec for the 93 million miles, after converting from decimal to standard seconds.  This is only about 2.4% off, so it isn’t too bad, but then he says this implies light travels 15.562085 earth radii per decimal second, which is very erroneous. He says the earth’s radius is 6369514 meters, which is close to the modern value of 6378000 meters, so that isn’t the source of the error. His claim corresponds to a speed of light equal to only about (1.147)10⁸ m/sec, which is low by a factor of 2.615. The deflection is proportional to the reciprocal of the square of this speed, so Soldner’s numerical value of ω = 0.0009798″ for the half-deflection of light near the Earth is too large by the factor 6.84. With the correct speed of light he would have gotten 0.0001432″. Strangely, his erroneous value of c doesn’t seem to have been used in his later calculation of deflection by the Sun.

Soldner then went on to consider the full deflection, 2ω, between in-coming and out-going asymptotes for light grazing the Moon as viewed from the Earth. He doesn’t actually give any numerical calculation or results, but he reports (not surprisingly) that this, too, was far too small to detect, since the Moon’s gravity is so slight.

Lastly, he considered the deflection for light rays near the surface of the Sun, although in lamentably ambiguous terms. In his own (translated) words, here is how he described the three cases (Earth, Moon, and Sun):

We [first] want to give an application of this formula [for the half-deflection angle ω] on earth, and investigate, to what extent a light ray is deflected from its straight line, when it passes by at the surface of earth…  If we want to investigate by the given formula, to what extent a light ray is deflected by the moon when it passes the moon and travels to earth, then we must double the value that was found by the formula [i.e., we must use 2ω], because the light ray that passes the moon and falls upon earth, describes two arms of the hyperbola…  If we substitute into the formula the acceleration of gravity on the surface of the sun, then we find ω = 0.84 arc seconds. If it were possible to observe the fixed stars very nearly at the sun, then we would have to take this into consideration.

His value of 0.84” corresponds roughly to the actual Newtonian ballistic value of 0.875” for the full deflection (2ω) passing the Sun, but he labels it as ω, meaning the half-deflection. Even Lenard agreed that, according to Soldner’s own formula, the value Soldner quotes is actually 2ω, which would be consistent with the assumption that he was referring to the full asymptotic deflection when he says “observe the fixed stars very nearly at the sun”. This can be interpreted to mean that we are observing, on Earth, the starlight grazing the Sun, just as he has described for light grazing the Moon. Soldner say this isn’t practical, presumably due to the brightness of the Sun, but it apparently didn’t occur to him that stars close to the Sun could be viewed during a total solar eclipse. If, however (as some have suggested), Soldner was really referring to the half-deflection as seen by some hypothetical Sun-dwelling creature, then his numerical value is too high by a factor of two. The Newtonian ballistic prediction is unambiguously ω = Gm/(v²r₀) = 0.437 arc seconds, but Soldner’s paper states that ω = 0.84 arc seconds, which is flatly erroneous. To correct the statement, he either needs to say ω = 0.42″ or else 2ω = 0.84″.

Indeed there is a manuscript copy of his paper in which someone has penciled in a “2” in front of Soldner’s designation of the solar deflection angle. When Lenard re-published the paper in the 20^th century he attributed the discrepancy to a misprint, assuming that Soldner was trying to give the full deflection between in-coming and out-going asymptotes. Others maintain that Soldner really mean ω as written, not 2ω, in which case his numerical result is just a mis-calculation from his equation.

There are also individuals who like to imagine that Soldner’s calculation actually gives ω = 0.84″, which would mean the full two-sided deflection is 2ω = 1.68″, very close to the relativistic value, but that is simply erroneous, because Soldner’s own derivation, as repeated by countless others, shows unambiguously that ω = 0.437 (slightly more than half Soldner’s value, due to his inaccurate values for the radius of the earth and acceleration of gravity, and whatever he used for the speed of light in his solar calculation, which he doesn’t say, but which obviously was not the grossly inaccurate value he used in his Earth calculation).

Incidentally, regarding Soldner’s value for the acceleration of gravity, many readers have been puzzled by his comment about a particular latitude. He says

If we take under the geographical latitude its square of the sine ⅓ (that corresponds to a latitude of 35° 16'), the earth radius by 6369514 meters, and the acceleration of gravity by 3.66394 meters (s. Traité de mécanique céleste par Laplace, Tome I, pag. 118): then, expressed in earth radii, g = 0.000000575231. I use this arrangement, to take the most recent and most reliable specifications of the size of earth's radius and the acceleration of gravity…

He is apparently attempting to account for the variation in the Earth’s radius and acceleration of gravity depending on the latitude. For example, due to the combined effect of the Earth’s oblate shape and its rotation, the local acceleration of gravity is about 0.5% less at the equator than at the poles. He claims to be using data for the latitude λ = 35° 16', which happens to be the angle for which sin(λ)² = 1/3, but one would probably need to consult Laplace to find out the significance of this choice. It may just be a latitute for which the radius and acceleration of gravity are easy to compute. In any case, it doesn’t appear to have much significance.

At the conclusion of the paper, Soldner says a few words acknowledging that some might question his treatment of light as consisting of material ballistic particles, referring to stellar aberration which, he says, is only possible if light rays consist of material particles. Presumably he’s alluding to Bradley’s account of aberration in terms of particles (like running in the rain). Soldner can perhaps be forgiven for not recognizing the difficulty that a classical ballistic theory has with the phenomena of interference, since Young was conducting his famous experiments at the very same time that Soldner was writing. Soldner concludes his defense by asserting that “we cannot think of things that exist and act on our senses without those things having the properties of matter” (which is obviously not true), and in support of this he cites Lucretius, who held that there is nothing but particles and the void.

Ironically, considering all the subtle factors of 2 lurking in Soldner’s calculation (which if done correctly is, after all, nothing but a simple exercise in Newtonian mechanics), it turned out that when developing general relativity Einstein first predicted in 1911 a deflection numerically equal to the Newtonian ballistic deflection (noting that “as the fixed stars in the parts of the sky near the Sun are visible during total eclipses of the Sun, this consequence of the theory may be compared with experience”), and then in 1915 discovered that taking the spatial curvature into account the full theory actually predicts twice the Newtonian ballistic value. As a result, modern anti-relativity enthusiasts have tried to exploit the ambiguities and idiosyncrasies in Soldner’s paper to suggest that Newtonian theory actually predicts the larger (observed) value. However, even Lenard, the advocate of Deutsche Physik and the person who championed Soldner, admitted that Newtonian ballistic theory – as confirmed by Soldner’s own equations – actually predicts the smaller value (which Lenard expected to be confirmed experimentally, despite Dyson’s and Eddington’s report), so either Soldner’s paper has a misprint or else Soldner was confused. It’s also ironic that Soldner was put forward as a victim of plagiarism, considering that Cavendish may have preceded Soldner, and Newton certainly preceded them both. There was nothing new in Soldner’s paper – aside from his mistakes. Also, it’s clear that only general relativity predicts the larger value. Furthermore, the classical ballistic concept of light had serious problems, which is why the Newtonian ballistic prediction of light deflection had not been considered viable. Indeed, the only nominally viable alternative to general relativity by 1919 was Nordstrom’s scalar theory, which predicted no deflection at all.

Return to MathPages Main Menu