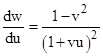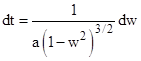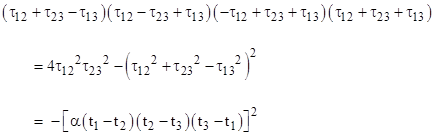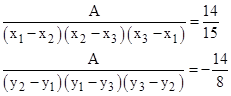Hyperbolic Motion and Parabolic Chords

“Now, gentlemen cosines, will you cease to throw parabolas and hyperbolas at each other’s heads? I want to understand the only interesting question in the whole affair. We shall follow one or the other of these curves? Good. But where will they lead us to?”  “Nowhere,” replied Nicholl.

                                                                                             Jules Verne

Let S be a standard system of inertial coordinates x,t, and let S′ denote another such system of coordinates x′,t′ moving at speed v in the positive x direction in terms of S. A particle p moving at speed u in terms of S′ is moving at speed w = (v+u)/(1+vu) in terms of S. From this we get

At a moment when the particle is at rest in S′ we have u = 0 and w = v, from which we get dw = (1 − v²)du.  Dividing both sides by dt gives dw/dt = (1 − v²)du/dt. Recalling that (dτ)² = (dt)² – (dx)² along the particle’s path, and that at this moment we have v = w = dx/dt, it follows that dτ/dt = √(1 – w²), so we have

The quantity dw/dt is the acceleration of the particle in terms of S, and the quantity du/dt is the acceleration of the particle in terms of the standard inertial coordinates in which the particle is momentarily at rest. The latter is called the proper acceleration, which we will denote with “a.

For constant proper acceleration a from rest at the origin, the above relation implies

Integrating this for a trajectory of constant proper acceleration “a” beginning from rest at the origin gives

Recalling that w = dx/dt, we can square both sides and re-arrange terms to give

Integrating this relation leads to the equation

and hence we have the equation of the hyperbolic path

This relation is identically satisfied if we put

for some path parameter τ. From this we get

and thus

which shows that the parameter τ is the proper time.  It’s also easy to see that every point on the hyperbolic locus is a constant proper distance of 1/a from the fulcrum event at x = −1/a, t = 0.

As a side note (related to curved paths and linear segments), consider the parabolic locus of events representing the trajectory of a path of constant coordinate acceleration α (noting that this is a realistic trajectory of a material particle only up to the speed of light). For any two events e_i and e_j on the parabola x = (α/2)t² the absolute interval between them has magnitude τ_ij that satisfies

For any three events e₁, e₂, e₃ on such a locus we can verify that

The quantity on the left side is just 16A² where A is Heron’s expression for the ordinary area of the triangle in the x,t plane with edge lengths τ₁₂, τ₂₃, and τ₁₃, Thus we have

An example is depicted in the figure below.

This formula is consistent with the simple expression for the (imaginary) area of a triangle in terms of the coordinates of its vertices

This has the requisite imaginary value if we take t as imaginary relative to x. If we substitute the parabolic expression t² for each x, we have the factorization

In the discussion above, the edge lengths τ_ij are evaluated using the Minkowski metric, but if we apply the Euclidean metric so that the edges are the ordinary lengths, we get the same results, except the sign of 16A² is positive, and hence the area is real-valued instead of imaginary, but with the same magnitude.

Every set of three events can be fit to a parabola with some parameter α and suitable origin, so these relations apply to any three events in Minkowski spacetime, and the analogous relations apply to any three points on the Euclidean plane. Of course, given the x,y coordinates of three points on the plane, we could fit then two a parabola with axis paralell to the x axis, or parallel to the y axis, i.e., to loci of the form x = (α_xy/2)y² or y = (α_yx/2)x². Thus, since the pairwise differences of the coordinates are invariant under translation, and the triangular area is the same, we have the signed area given by

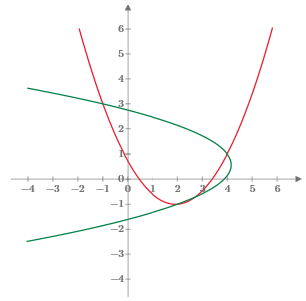
To illustrate, consider the three points in the Euclidean x,y plane with (x,y) coordinates (-1,3), (2,-1), and (4,1). The two parabolas are

Since we define the quadratic coefficient as α/2, we have α_xy = 14/15 and α_yx = -14/8. These parabolas are plotted in the figure below.

The area of the triangle with those three vertices is A = 7, and we have

Note that we transposed 1 and 2 indixes in the secong expression because we reverse clockwise and counter-clockwise (and hence the sign of the area) when we transpose x and y.

Return to MathPages Main Menu