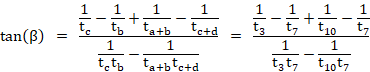|
Advent Calander |
|
|
|
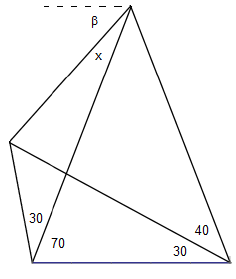
Consider the quadrilateral with diagonals shown below. |
|
|
|
|
|
|
|
The angles across the bottom are marked in degrees, and our objective is to determine the value of the angle denoted by ‘x’. The angle denoted as β is the angle made by the upper-left edge with the dashed line parallel to the base edge. This particular quadrilateral has special symmetries leading to some simple solutions, e.g., it contains the isosceles triangle with base angles of 70 degrees, and the other two specified angles are both 30 degrees. (On the other hand, the diagonals are not perpendicular, so this isn’t in the special class of adventitious quadrilaterals.) We won’t take advantage of any of these special symmetries, we will determine the solution using the fully general trigonometric method described in Angular Angst and in Adventitious Solutions. |
|
|
|
All the angles are multiples of 10 degrees, which is α = π/18. For convenience we will let t denote tan(α), and we will denote by t2, t3, … the values tan(2α), tan(3α), ... respectively. In these terms we can write the well-known trigonometric identities |
|
|
|
|
|
|
|
and so on. In each case, the coefficients in the numerator and denominator are every second binomial coefficient with alternating signs. Letting a,b,c,d denote the angles 30, 70, 30, 40 respectively across the base, and using the formula from Angular Angst, the value of the angle β is |
|
|
|
|
|
|
|
Numerically, taking the inverse tangent, we can calculate that β equals 50 degrees, at least to the precision of our calculations, which implies that x is 20 degrees (since the 70 degree diagonal cuts the two parallel lines, base and dashed). To prove that this is the exact solution, we can algebraically evaluate |
|
|
|
|
|
|
|
As discussed in the note on linear fractional transformations, the quantities tan(kπ/18) for k=1,3,5,… are the roots of the polynomial with coefficients taken from the 9th row of the binomial coefficients, every second coefficient, with alternating signs, i.e., |
|
|
|
|
|
|
|
The value of tan(π/18) is a root of the right-hand factor, so the preceding expression vanishes, meaning that tan(β) = tan(50°), which was to be shown. |
|
|
|
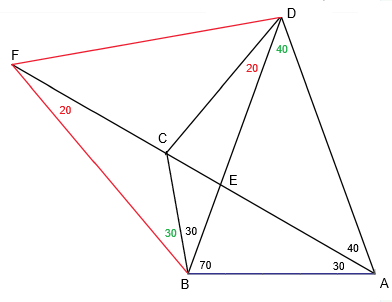
As noted above, this particular example has symmetries that enable a simpler solution. Suppose we construct an equilateral triangle on the segment BD, with the other vertex at F, as shown below. |
|
|
|
|
|
|
|
Since ADB is isosceles, AD equals BD, and since BDF is equilateral, DF equals BD, so AD equals DF, and therefore ADF is isosceles. Hence the base angles of ADF are [180 – (40+60)]/2, which equals 40 degrees, proving that AC and AF lie along the same line. Since angle DFB is 60 deg, and angle DFC is 40 degrees, it follows that angle BFC equals 20 degrees. Also, BCD and BCF are similar triangles, so angle EDC is 20 degrees, which was to be found. |
|
|