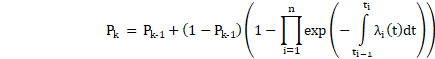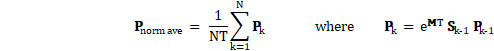Changes in Appendix F of AC 25.1309-1B

In December 2022 the FAA issued a Notice of Proposed Rulemaking (NPRM) that was accompanied by a draft update to Advisory Circular (AC) 25.1309 for public comment. One of the key parts of this AC is Appendix F, which defines the normalized average probability that is to be compared with the specified quantitative thresholds to determine compliance with the regulation. The intent was to harmonize with the calculation in the 2002 Arsenal draft AC and the EASA AMC 25.1309 that have been in use for over 20 years. Indeed, the description of the calculation in the NPRM draft that was circulated for public comment was essentially identical to the corresponding sections of those earlier versions (with the exception of a parenthetical statement in the NPRM draft related to normalization, which we discuss in another article).

However, in the published version of AC 25.1309-1B, released in August of 2024, the description of the probability calculation in Appendix F was extensively re-written, particularly Section F.4, rendering it incoherent. If it was a computer program, it wouldn’t compile. For example, a recurrence expression with a free index is treated as if it has some definite value, so it doesn’t even parse mathematically. This and other inconsistencies make it impossible for applicants to determine the “Average Probability per Flight Hour” by following the steps in the published Appendix F as written.

We’ll describe the problems with the published Appendix F below. For context, in Part I we review the original calculation of normalized average probability (also called “Average Probability per Flight Hour”) as described clearly and correctly in the 2002 Arsenal draft, the EASA AMC, and the 2022 NPRM draft, which are all essentially identical (aside from the misconceived statement about normalization in the NPRM draft). In Part II we describe the re-written version of Appendix F in the published AC.

I.  Review of Arsenal, EASA, and NPRM AC 25-1309 Calculation

For definite citations in this section, we’ll refer to the Arsenal draft. The process of calculating the quantity referred to as "Average Probability per Flight Hour" for a Failure Condition is described in Appendix 3 of the Arsenal as a four-step process, based on the assumption that the life of an aircraft is a sequence of "Average Flights".  (It’s worth noting that the name of the quantity being calculated was intentionally presented in the Arsenal in quotation marks, to signal that it is the label of a specially defined quantity, which is an important fact that was lost sight of in the NPRM draft.) These four steps are described below.

Step 1: Determination of the "Average Flight"

This is described in sub-paragraph “a”.  The applicant should estimate the average flight duration and average flight profile for the fleet of aircraft to be certified.  The duration of each flight phase (e.g. takeoff, climb, cruise, descent, approach and landing) in the "Average Flight" should be based on the average flight profile.  The applicant then determines the failure rate function for each element of the system during each phase (which may be different).

Step 2: Calculation of the probability of a Failure Condition for a certain "Average Flight"

This is described in sub-paragraph “b”.  This section gives the formula for the probability of a given fault being present at some time on the kth flight recursively in terms of the probability at the start of that flight.  The probability at the start of the kth flight equals zero for an element that is checked good at the beginning of the flight, and otherwise equals the probability at the end of the (k−1)th flight. The Arsenal AC gives these as two separate formulas, but they are both entailed (for a single element) by the recursive formula

where P_k is the probability of the failure condition of this element being present by the end of the kth flight (called “a certain flight”), and λ_i(t) is the failure rate function during the ith of n phases. (For the derivation of this standard formula, see “The Failure Rate Function”.) If the element is checked and (if necessary) repaired prior to the kth flight, then the prior probability P_k−1 is set to 0, so this formula represents both formulas given in this section of the Arsenal description.  This formula can be written in vector notation (for the two states, healthy or failed, of a single element) as

where P_k denotes the kth probability state vector (representing the probabilities of the states of the cutset), M is the mean failure rate matrix, S_k is the kth repair transition matrix, and T is the average flight time.  (See “The Arsenal Companion” for a detailed explanation of this correspondence.) The same equation applies to a model with any number of states, representing an entire failure condition (cutset), with each element treated as specified. Note that this Arsenal calculation is nothing but the standard solution of dP/dt = MP for a given combination of failures, as discussed in Section I.4.10 and I.6 of ARP 4761A, as well as in innumerable textbooks.

Step 3: Calculation of the "Average Probability per Flight" of a Failure Condition

This is described in sub-paragraph “c”.  The average of the probabilities on each of the N flights, which we will denote as P_ave, is given (again in vector notation) by

The Arsenal gives this formula for just the scalar value of the fully-failed component of the state vector, but it’s convenient to compute the probabilities for all the states.

Step 4: Calculation of the "Average Probability Per Flight Hour" of a Failure Condition

This is described in sub-paragraph “d”.  The normalized average probability is defined as the average probability divided by the average flight length T, so

The relevant component of the state vector is the one representing the joint failure of all the elements in the combination (cutset), i.e., the probability that the cutset is satisfied.  The probability of the union of multiple cutsets is given by inclusion-exclusion, or just simple summation for rare events.  As stated in the Arsenal, the resulting quantitative value should be used in conjunction with the hazard category/effect established by the hazard analysis to determine if it is compliant for the Failure Condition being analyzed.

In summary, following these four steps, the quantity “Average Probability per Flight Hour” (i.e., the normalized average probability) for any given cutset is defined in the Arsenal AC and the EASA AMC and the FAA’s 2022 NPRM draft AC as

with M and S denoting the mean failure rate matrix and the inspect/repair transition matrix respectively, T is the average flight duration, and N is the number of flights in the life of the airplane. This accounts for all scheduled inspection/repair strategies (including latencies), phase dependencies, required sequencing, etc. More background and some example calculations are provided in the articles on “Normalized Average Probability”, “Probability for Regulatory Requirements” and “Latencies and Periodic Repairs”.

II.  Review of AC 25.1309-1B Appendix F, Post NPRM

One of the public comments on the 2022 NPRM draft AC was a request to include worked examples of the calculation defined in Appendix F, particularly the steps in F.3 and F.4, to “prevent confusion on how to correctly apply the equations”. This was not a request to change the calculation, let alone to change what was being calculated (which has been stable for decades and is unobjectionable), but merely to carry out the steps of the Arsenal calculation on some simple examples.  This was admittedly a somewhat obtuse comment, since it didn’t identify any particular aspect of the calculation or wording that was perceived to be unclear.  In response, the FAA declined to provide any worked examples of the steps of the Arsenal calculation (on the grounds that ARP 4761 contains such examples - which it does not, as explained in another article), but instead substantially re-wrote the section, changing not only how the calculation is to be performed, but what it is attempting to calculate, and in the process, mangling the section so it no longer defines a coherent calculation of anything. This drastic and extensive alteration of the key section of the AC that is supposed to define the fundamental compliance criteria for 25.1309 was introduced without any public comment.

Note: In this article we confine ourselves to discussing the problems with the actual published AC, which has been rendered incoherent by the re-write.  In another article we discuss the problems with what may have been the intended change, which would also have been fundamentally wrong, but for a different reason.

The overview in the published F.1 is essentially the same as in the corresponding sections of the Arsenal, EASA, and NPRM versions, describing the calculation in terms of the same simple four-step process described in Part I of this article. However, the description of the third step in F.4 of the published AC has been drastically altered, and the alteration was mangled, such that it no longer parses as a meaningful mathematical calculation. The change is not subtle, as can be seen from the screen cap of the NPRM version and the published version of the most affected section below.

The title of the third step presented in F.4 is still given in the overview section (F.1) as

Calculate the average probability per flight of a failure condition.

But, as shown in the extract above, in the published AC this is now inconsistent with the title of this step in F.4, which has been changed to

Calculation of the “Probability per Flight” of a Failure Condition over a period of N flights.

The word “average” has been removed from the title of this step, and from some parameter names as well, even though, in the Arsenal, the entire purpose of this step is simply to compute the average of the probabilities of the failure condition being present on each of the N flights. (See the related article for a discussion of the English meanings of the word “occur”.) The recurrence relation for computing the probability of the failure condition for each flight is provided in Section F.3, and the text of F.4 says “the probability of the failure condition for each flight … should be calculated, summed up, and divided by the number of flights during that period”.  As explained in detail below, with the drastic changes introduced (post-NPRM) in the published AC, the section doesn’t even claim to be doing anything like this.

Step 3 in the published AC has been split into two parts, depending on whether “the element is checked operative at the beginning of each flight”.  However, the individual elements have already been treated in Step 2 of the Arsenal, whereas Step 3 of the Arsenal is dealing with the overall failure condition (or cutset), which in general consist of multiple elements, some of which may be latent and others active.  It is not generally possible to classify a failure condition as either checked operative or not checked operative at the beginning of each flight. Neither the Arsenal/NPRM draft nor the EASA AMC are dealing with individual elements in this step, they simply compute the average of the probabilities of the entire failure condition for the N flights, as explicitly stated in the original title and text of the section. The published AC is doing something completely different in this step, contrary to the original title and purpose of the step.

The next part of Step 3 in the published AC is mathematically incoherent. Recall that the recurrence relation provided in Step 2 for the probability of elements that comprise the overall failure condition gives P_k as a function of P_k−1. The average of these is found by summing the P_k values for k = 1 to N, and dividing by N.  The published AC still does this as well -- but only for “active elements”. For the “latent” case (again, overlooking that this is an unintelligible bifurcation for overall failure conditions to be addressed in this step) it replaces the calculation of the average of the P_k values with the following expression (where we have denoted P_prior by P_k−1)

This is mathematically senseless, because the left side is a definite value whereas the “k” on the right side is a free index, meaning it has no definite value. For any given flight, for which the probability of the failure condition is P_k, the value of P_k−1 is the probability of the failure condition at the end of the prior flight (reset for repairs), but this doesn’t specify which two consecutive flights it is referring to. It is a generic recursive relation, and k represents an unspecified index in the range from 1 to N. The recurrence relation, given in Step 2, enables us to compute all the values P₁, P₂, P₃, …, P_N, and we can then compute the average of these values, as prescribed in the Arsenal, NPRM, and EASA versions of the calculation. (Refer to the description in Part I above.) Choosing just one of these probabilities, without specifying which one, and dividing it by N, is both underspecified and nonsensical. Even if the published AC were revised, say by specifying a particular value of k such as (say) k = N, this would still not equal the average of the probabilities, which is what the Arsenal, NPRM, and EASA versions are calculating in this Step, and what even the published AC itself claims (in the overview) to be computing in this Step.

It should be emphasized (again) that, in general, the re-written “calculation” described in Appendix F of the published AC cannot even be carried out, because it isn’t an executable expression. (Contrast this with the expression in Step 3 in the Arsenal, as described in Part I above, in which the free k index is summed from 1 to N to yield the required value.) Also, the section that, in the Arsenal, is taking the average of the probabilities of the overall failure condition, has been changed so that it just gives another (nonsensical) pseudo-operation involving the individual elements, whose evaluation has already been fully explained in the previous section. Note that this step of the published AC cannot be dealing just with elements (despite what it says), because the computed quantity from this step, after simply dividing by average flight duration in Step 4, is the final result for the overall failure condition.

Hence the published AC is incoherent on multiple levels, and can’t be used to make any compliance showings at all.  The only way to “fix” it would be to revert to the Arsenal/NPRM/EASA version, which (as described in Part I above) gives a simple, straightforward, and correct calculation of the normalized average probability in all possible circumstances, for both active and latent faults, with any possible repair strategies, phase dependencies, etc.  Harmonizing on this calculation was the ostensible purpose of the new rulemaking activity in the first place.

Although the published AC is strictly unusable, an advisory circular is generally regarded as a means, but not necessarily the only means, of showing compliance. Applicants may propose to continue to use the correct mathematical expressions for normalized average probability given in the draft Arsenal (and the NPRM) advisory circular and the EASA AMC until the mistakes introduced in the released version of AC 25.1309-1B are fixed.  As discussed in another article, the AC can be repaired simply by restoring the Arsenal calculation.

Return to MathPages Main Menu