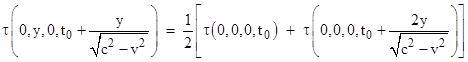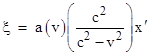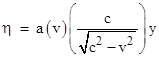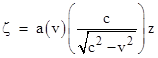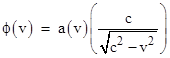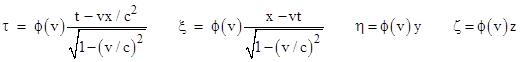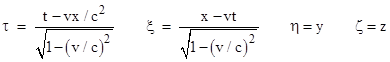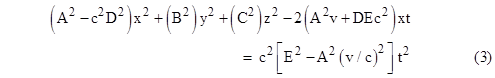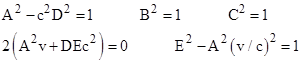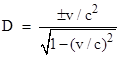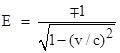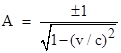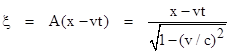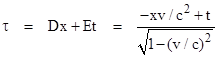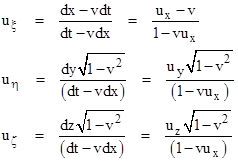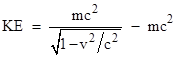|
1.6 A More Practical Arrangement |
|
|
|
It is known that Maxwell’s electrodynamics – as usually understood at the present time – when applied to moving bodies, leads to asymmetries which do not appear to be inherent in the phenomena. |
|
A. Einstein, 1905 |
|
|
|
In the first section of his 1905 paper "On the Electrodynamics of Moving Bodies" Einstein noted that we could assign to each event the time reading of a clock resting at the origin of a system of spatial coordinates when light from that event reaches the clock, but this has the disadvantage of making the time coordinates dependent on the choice of spatial origin. The same would be true if we assigned the reading of the clock to each event when light from the clock reaches that event. These methods give time coordinates that are offset – either leading or lagging – by the light transit time to or from the origin. We could eliminate the dependence on the choice of spatial origin by taking the average of the two, i.e., assigning the origin clock time to each event that is temporally half-way between the leading and lagging events at any fixed spatial location. However, this is valid only if the speed of light (or, more generally, the signal) is isotropic in terms of those coordinates. According to Lorentz, this would apply only for a system of coordinates at rest in the ether, and he regarded the time coordinate of this system as the “true” time coordinate for all other systems as well, even though his theory implied that those other systems would not constitute inertial coordinate systems, because mechanical inertia would not be isotropic in terms of those systems. In his 1905 paper, Einstein said "We arrive at a much more practical arrangement by means of the following considerations". |
|
|
|
Einstein argued that what Lorentz regarded as artificial coordinate systems (in terms of which Maxwell’s equations are invariant) are none other than the actual inertial coordinate systems, meaning they are the systems of coordinates in which the equations of Newtonian mechanics hold good “to the first approximation” (i.e., in the low speed limit). To deduce the relationship between such coordinate systems he proceeded quite differently from Lorentz, basing his argument on much simpler and more fundamental principles. |
|
|
|
First he described an operational way of establishing an inertial coordinate system, including the time coordinate (although he originally referred to time verbally as a separate parameter rather than as a fourth coordinate). As discussed in Section 1.3, the inertia-based coordinate systems of Galileo and Newton had always included an operational definition of the time coordinate, necessary to make mechanical inertia isotropic (equal action and reaction), but too little attention had been paid to this. Einstein contributed to the eventual clarification of this fact, although he did so by using light signals to synchronize separate clocks, which made it easily confused with Poincare’s earlier comments about the correspondence between Lorentz’s local time and the time given by light synchronization. This by itself is circular, because Lorentz’s local time is defined as the time necessary for Maxwell’s equations to hold good, which automatically entails that light speed is isotropic in terms of those coordinates. Thus Poincare’s observation, although suggestive, did not actually add anything substantially new to the understanding of the physical significance of Lorentz’s local time. |
|
|
|
In contrast, Einstein’s presentation entails that mechanical inertia is isotropic in terms of those same coordinates, and hence those systems really are the inertia-based systems. This point was somewhat obscured in his 1905 paper by his decision to use light signals, although in later writings he acknowledged that any inertially symmetrical signals – such as pairs of identical material objects acting against each other with equal force from rest in opposite directions – can be used. (The special attribute of light in this regard is that it has no mass and therefore no rest frame, so we can dispense with the “from rest” condition.) |
|
|
|
Having clarified (to an extent) the operational meaning of inertia-based coordinate systems, Einstein then expressed two empirically-based principles on which his derivation of the Lorentz transformation would be based: |
|
|
|
1. The laws by which the conditions of physical systems change are independent of which of two coordinate systems in homogeneous translational movement relative to each other these changes in status are referred. |
|
|
|
2. Each ray of light moves in "the resting" coordinate system with the definite speed c, independently of whether this ray of light is emitted from a resting or moving body. Here speed = (optical path) / (length of time), where "length of time" is to be understood in the sense of the definition in § l. |
|
|
|
In the first of these propositions the “coordinate systems” must be the inertia-based systems discussed above, because without this stipulation, the proposition is false. For example, coordinate systems related by Galilean transformations are “in homogeneous translational movement relative to each other”, and yet the laws by which physical systems change (e.g., Maxwell’s equations) are manifestly not independent of the choice of such coordinate systems. So the restriction to coordinate systems in terms of which the homogeneous and isotropic equations of mechanics hold good is essential. However, once we have imposed this restriction, the proposition becomes tautological, at least for mechanics. The real content of Einstein’s first “principle” is therefore the assertion that the other laws of physics (e.g., the laws of electrodynamics) in homogeneous and isotropic form hold good in precisely the same set of coordinate systems in terms of which the laws of mechanics hold good. This is also the empirical content of the failure of the attempts to detect the Earth’s absolute motion through the electromagnetic ether. Thus Einstein’s first principle simply re-asserts Galileo’s claim that all effects of uniform rectilinear motion on the laws of physics can be “transformed away” by a suitable choice of coordinate systems. |
|
|
|
The second principle, too, applies only to a (local) inertia-based coordinate system, and only in vacuum, and Einstein chose to express it in terms of just one such system, which his readers would have identified with the rest frame of Lorentz’s ether, even though Einstein is stipulating a vacuum and excluding any efficacious ether. Skeptics sometimes suspect that this light-speed principle is circular, because (as noted above) Einstein used light signals to establish the coordinates, so the second principle states that the speed of light is c in terms of coordinates defined such that the speed of light is c. It would have been more clear (as he later acknowledged) to use mechanical inertia to establish simultaneity of inertial coordinate systems by (for example) using two identical and mutually repulsive particles released from rest at the midpoint between two clocks. Equivalently we could use sound waves from the midpoint of a solid rod to synchronize clocks at the ends. This makes it clear that the physical content of the second principle is that the propagation speed of light is isotropic in terms of the same coordinates in which mechanical inertia is isotropic. |
|
|
|
This second principle was ostensibly based on all the experimental results that are consistent with the Maxwell-Lorentz equations for the ether frame. Combining this principle with the first, along with the tacit premise that the vacuum does not discriminate between different states of motion, Einstein immediately infers that the speed of light is invariant with respect to every system of inertial coordinates. This extension is based on the unspoken and non-trivial premise about the vacuum, so later authors have often simply taken the general proposition as the second principle. (See Section 3.1 for more discussion of the foundations of Einstein’s principles.) Of course, Einstein’s weaker form of the second principle has significant content, since we are not guaranteed that the speed of every pulse of light is isotropic and homogeneous in terms of any (let alone every) system of inertial coordinates. For example, it would not be in a classical emission theory. |
|
|
|
After stating his two principles, Einstein goes on to derive the relationship (now called the Lorentz transformation) between inertia-based coordinate systems. The actual detailed derivation presented in Einstein’s 1905 paper appears somewhat circuitous and overly elaborate today, but it’s worthwhile to follow his reasoning, partly for historical interest, and partly to contrast it with the more direct and compelling derivations presented in subsequent sections. |
|
|
|
Following Einstein’s original derivation, we begin with an inertial (and Cartesian) coordinate system called K, with the coordinates x, y, z, t, and we posit another system of inertial coordinates denoted as k, with the coordinates ξ, η, ζ, τ. The spatial axes of these two systems are aligned, and the spatial origin of k is moving in the positive x direction with speed v in terms of K. We then consider a particle at rest in the k system, and note that for such a particle the x and t coordinates (i.e., the coordinates in terms of the K system) are related by xʹ = x − vt for some constant xʹ. We also know the y and z coordinates of such a particle are constant. Hence each stationary spatial position in the k system corresponds to a set of three constants (xʹ,y,z), and we can also assign the time coordinate t to each event. |
|
|
|
Interestingly, the system of variables xʹ,y,z,t constitute a complete coordinate system, related to the original system K by a Galilean transformation xʹ = x − vt, yʹ=y, zʹ=z, tʹ=t. Thus, just as Lorentz did in 1892, Einstein began by essentially applying a Galilean transformation to the original “rest frame” coordinates to give an intermediate system of coordinates, although Einstein’s paper makes it clear that this is not an inertial coordinate system. |
|
|
|
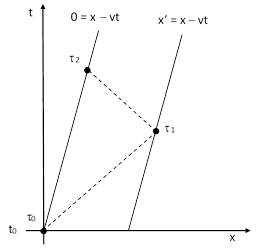
Now we consider the values of the τ coordinate of the k system as a function of xʹ,y,z,t for any stationary point in the k system. Suppose a pulse of light is emitted from the origin of the k system in the positive x direction at time τ0, it reaches the point corresponding to xʹ,y,z at time τ1, where it is reflected, arriving back at the origin of the k system at time τ2. This is depicted in the figure below. |
|
|
|
|
|
|
|
Recall that the ξ, η, ζ, τ coordinates are defined as inertial coordinates, meaning that inertia is homogeneous and isotropic in terms of these coordinates. Also, all experimental evidence (such as all "the unsuccessful attempts to discover any motion of the earth relatively to the 'light medium'") indicates that the speed of light is isotropic in terms of any inertial coordinate system. Therefore, we have t1 = (t0 + t2)/2, so the τ coordinate as a function of xʹ,y,z,t satisfies the relation |
|
|
|
|
|
|
|
Differentiating both sides with respect to the parameter xʹ, we get (using the chain rule) |
|
|
|
|
|
|
|
Now, it should be noted here that the partial derivatives are being evaluated at different points, so we would not, in general, be justified in treating them interchangeably. However, Einstein has stipulated that the transformation equations are linear (due to homogeneity of space and time), so the partial derivatives are all constants and unique (for any given v). Simplifying the above equation gives |
|
|
|
|
|
|
|
At this point, Einstein alludes to analogous reasoning for the y and z directions, but doesn’t give the details. Presumably we are to consider a pulse of light emanating from the origin and reflecting at a point xʹ = 0, y, z = 0, and returning to the origin. In this case the isotropy of light propagation in terms of inertial coordinates implies |
|
|
|
|
|
|
|
In this equation we have made use of the fact that the y component of the speed of the light pulse (in terms of the K system) as it travels in either direction between these points, which are stationary in the k system, is (c2 – v2)1/2. Differentiating both sides with respect to y, we get |
|
|
|
|
|
|
|
and therefore ∂τ/∂y = 0. The same reasoning shows that ∂τ/∂z = 0. Now the total differential of τ(xʹ,y,z,t) is, by definition |
|
|
|
|
|
|
|
and we know the partial derivatives with respect to y and z are zero, and those with respect to xʹ and t are in a known ratio, so for any given v we can write |
|
|
|
|
|
|
|
where a(v) is as yet an undetermined function. Incidentally, Einstein didn’t write this expression in terms of differentials, but he did state that he was “letting xʹ be infinitesimally small”, so he was essentially dealing with differentials. On the other hand, the distinction between differentials and finite quantities matters little in this context, because the relations are linear, and hence the partial derivatives are constants, so the differentials can be trivially integrated. Thus we have |
|
|
|
|
|
|
|
Einstein then used this result to determine the transformation equations for the spatial coordinates. The ξ coordinate of a pulse of light emitted from the origin in the positive x direction is related to the τ coordinate by ξ = cτ (which Einstein justifies by saying it is “required by the principle of the constancy of the velocity of light in combination with the principle of relativity”). Substituting for τ from the preceding formula gives, for the ξ coordinate of this light pulse, the expression |
|
|
|
|
|
|
|
We also know that, for this light pulse, the parameters t and xʹ are related by t = xʹ/(c−v), so we can substitute for t in the above expression and simplify to give the relation between ξ and xʹ (both of which, we remember, are constants for any point at rest in k) |
|
|
|
|
|
|
|
We can choose xʹ to be anything we like, so this represents the general relation between these two parameters. Similarly the η coordinate of a pulse of light emanating from the origin in the η direction is |
|
|
|
|
|
|
|
but in this case we have xʹ = 0 and, as noted previously, t = y/(c2-v2)1/2, so we have |
|
|
|
|
|
|
|
and by the same token |
|
|
|
|
|
|
|
If we define the function |
|
|
|
|
|
|
|
and substitute x – vt for xʹ, the preceding results can be summarized as |
|
|
|
|
|
|
|
At this point Einstein observes that a sphere of light expanding with the speed c in terms of the x, y, z, t coordinates transforms to a sphere of light expanding with speed c in terms of the ξ, η, ζ, τ coordinates. In other words, |
|
|
|
|
|
|
|
As Einstein says, this “shows that our two fundamental principles are compatible”, i.e., it is possible for light to propagate isotropically with respect to two relatively moving systems of inertial coordinates, provided we allow the possibility that the transformation from one inertial coordinate system to another is not exactly as Galileo and Newton surmised. |
|
|
|
To complete the derivation of the Lorentz transformation, it remains to determine the function ϕ(v). Einstein considers a two-fold application of the transformation, once with the speed v in the positive x direction, and then again with the speed v in the negative x direction. The result should be the identity transformation, i.e., we should get back to the original coordinate system. (Strictly speaking, this assumes the property of “memorylessness”, discussed below.) If we apply the above transformation twice, once with parameter v and once with parameter −v, each coordinate is ϕ(v)ϕ(−v) times the original coordinate, so we must have |
|
|
|
|
|
|
|
Finally, Einstein concludes by “inquiring into the signification of ϕ(v)”. He notes that a segment of the η axis moving with speed v perpendicular to its length (i.e., in the positive x direction) has the length y = η/ϕ(v) in terms of the K system coordinates, and by “reasons of symmetry” (i.e., spatial isotropy) this must equal η/ϕ(−v), because it doesn’t matter whether this segment of the y axis is moving in the positive or the negative x direction. Consequently we have ϕ(v) = ϕ(−v), and therefore ϕ(v) = 1, so he arrives at the Lorentz transformation |
|
|
|
|
|
|
|
This somewhat laborious and awkward derivation is interesting in several respects. For one thing, one gets the impression that Einstein must have been experimenting with various methods of presentation, and changed his nomenclature during the drafting of the paper. For example, at one point he says “a is a function ϕ(v) at present unknown”, but subsequently a(v) and ϕ(v) are defined as different functions. At another point he defines x′ as a Galilean transform of x (without explicitly identifying it as such), but subsequently uses the symbol x′ as part of the inertial coordinate system resulting from the two-fold application of the Lorentz transformation. In addition, he somewhat tacitly makes use of the invariance of the light-like relation x2 + y2 = c2t2 in his derivation of the transformation equations for the y coordinate, but doesn’t seem to realize that he could just as well have invoked the invariance of x2 + y2 + z2 = c2t2 to make short work of the entire derivation. Instead, he presents this invariance as a consequence of the transformation equations – despite the fact that he has tacitly used the invariance as the basis of the derivation (which of course he was entitled to do, since that invariance simply expresses his “light principle”). |
|
|
|
Perhaps not surprisingly, some readers have been confused as to the significance of the functions a(v) and ϕ(v). For example, in a review of Einstein’s paper, A. I. Miller writes |
|
|
|
Then, without prior warning Einstein replaced a(v) with ϕ(v)/(1-(v/c)2)1/2… But why did Einstein make this replacement? It seems as if he knew beforehand the correct form of the set of relativistic transformations… How did Einstein know that he had to make [this substitution] in order to arrive at those space and time transformations in agreement with the postulates of relativity? |
|
|
|
This suggests a misunderstanding, because the substitution in question is purely formal, and has no effect on the content of the equations. The transformations that Einstein had derived by that point, prior to replacing a(v), were already consistent with the postulates of relativity (as can be verified by substituting them into the Minkowski invariant). It is simply more convenient to express the equations in terms of ϕ(v), which is the entire coefficient of the transformations for y and z. One naturally expects this coefficient to equal unity. |
|
|
|
Even aside from the inadvertent changes in nomenclature, Einstein’s derivation is undeniably clumsy, especially in first applying what amounts to a Galilean transformation, and then deriving the further transformation needed to arrive at a system of inertial coordinates. It seems clear that he was influenced by Lorentz’s writings, even to the point of using the same symbol b for the quantity 1/(1-(v/c)2)1/2, which Lorentz used in his 1904 paper. (Surprisingly, years later Einstein wrote to Carl Seelig that in 1905 he had known only of Lorentz’s 1895 paper, but not his subsequent papers, nor Poincare’s 1905 paper on the subject.) |
|
|
|
In a review article published in 1907 Einstein had already adopted a more economical derivation, dispensing with the intermediate Galilean system of coordinates, and making direct use of the lightlike invariant expression, similar to the standard derivation presented in most introductory texts today. To review this now standard derivation, consider (again) Einstein’s two systems of inertial coordinates K and k, with coordinates denoted by (x,y,z,t) and (ξ,η,ζ,τ) respectively, and oriented so that the x and ξ axes coincide, and the xy plane coincides with the ξη plane. Also, as before, the system k is moving in the positive x direction with fixed speed v relative to the system K, and the origins of the two systems momentarily coincide at time t = τ = 0. |
|
|
|
According to the principle of homogeneity, the relationship between the two sets of coordinates must be linear, so there must be constants A1 and A2 (for a given v) such that ξ = A1x + A2 t. Furthermore, if an object is stationary relative to k, and if it passes through the point (x,t) = (0,0), then it's position in general satisfies x = vt, from the definition of velocity, and the ξ coordinate of that point with respect to the k system is 0. Therefore we have ξ = A1(vt) + A2t = 0. Since this must be true for non-zero t, we must have A1v + A2 = 0, and so A2 = -A1v. Consequently, there is a single constant A (for any given v) such that ξ = A(x-vt). Similarly there must be constants B and C such that η = By and ζ = Cz. Also, invoking isotropy and homogeneity, we know that τ is independent of y and z, so it must be of the form τ = Dx + Et for some constants D and E (for a given v). It only remains to determine the values of the constants A, B, C, D, and E in these expressions. |
|
|
|
Suppose at the instant when the spatial origins of K and k coincide a spherical wave of light is emitted from their common origin. At a subsequent time t in the first frame of reference the sphere of light must be the locus of points satisfying the equation |
|
|
|
|
|
|
|
and likewise, according to our principles, in the second frame of reference the spherical wave at time t must be the locus of points described by |
|
|
|
|
|
|
|
Substituting from the previous expressions for the k coordinates into this equation, we get |
|
|
|
|
|
|
|
Expanding these terms and rearranging gives |
|
|
|
|
|
|
|
The equality of the speed of light in terms of both systems of coordinates implies that an expanding spherical wave of light in one system is also an expanding spherical wave of light in the other system, so the coefficients of equation (3) must be proportional to the coefficients of equation (1). Strictly speaking, the constant of proportionality is arbitrary, representing a simple re-scaling, so we are free to impose an additional condition, namely, that the transformation with parameter +v followed by the transformation with parameter –v yields the original coordinates, and by the isotropy of space these two transformations, which differ only in direction, must have the same constant of proportionality. Thus the corresponding coefficients of equations (1) and (3) must not only be proportional, they must be equal, so we have |
|
|
|
|
|
|
|
Clearly we can take B = C = 1 (rather than −1, since we choose not to reflect the y and z directions). Dividing the 4th of these equations by 2, we're left with the three equations in the three unknowns A, D, and E: |
|
|
|
|
|
|
|
Solving the first equation for A2 and substituting this into the 2nd and 3rd equations gives |
|
|
|
|
|
|
|
Solving the first for E and substituting into the 2nd gives a single quadratic equation in D, with the roots |
|
|
|
|
|
|
|
Substituting this into either of the previous equations and solving the resulting quadratic for E gives |
|
|
|
|
|
|
|
Note that the equations require opposite signs for D and E. Now, for small values of v/c we expect to find E approaching +1 (as in Galilean relativity), so we choose the positive root for E and the negative root for D. Finally, from the relation A2 − c2 D2 = 1 we get |
|
|
|
|
|
|
|
Again selecting the positive root, we have the Lorentz transformation |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Naturally with this transformation we can easily verify that |
|
|
|
|
|
|
|
so this quantity is the squared "absolute distance" from the origin to the point with K coordinates (x,y,z,t) and the corresponding k coordinates (ξ,η,ζ,τ), which confirms that the absolute spacetime interval between two points is the same in both frames. Notice that equations (1) and (2) already implied this relation for null intervals. In other words, the original premise was that if x2 + y2 + z2 - c2t2 equals zero, then ξ2 + η2 + ζ2 − c2τ2 also equals zero. The above reasoning show that a consequence of this premise is that, for any arbitrary real number s2, if x2 + y2 + z2 - c2t2 equals s2, then ξ2 + η2 + ζ2 − c2τ2 also equals s2. Therefore, this quadratic form represents an absolute invariant quantity associated with the interval from the origin to the event (x,y,z,t). |
|
|
|
Given the Lorentz transformation it is easy to determine the full velocity composition law for two systems of aligned coordinates K and k, the latter moving in the positive x direction with velocity v relative to the former. We can without loss of generality make the origins of the two systems both coincide with a point P0 on the subject worldline, and let P1 denote a subsequent point on that worldline with K system coordinates dt,dx,dy,dz. The velocity components of that worldline with respect to K are ux = dx/dt, uy = dy/dt, and uz = dz/dt. The coordinates of P1 with respect to the k system are given by the Lorentz transformation (in units with c = 1) for a simple boost v in the x direction: |
|
|
|
|
|
|
|
Therefore, the velocity components of the worldline with respect to the k system are |
|
|
|
|
|
|
|
This illustrates the value of Einstein’s “more practical arrangement”, based on the recognition that inertial coordinate systems are related by Lorentz transformations. From this single dynamical premise, many results follow by pure kinematics. |
|
|
|
As an aside, notice that light-speed isotropy with respect to the rest frame of the source is what we would expect if light was a stream of inertial corpuscles (as suggested by Newton), whereas the independence of the speed of light from the motion of its source is what we would expect if light was a wave in a medium. Thus, just as in quantum mechanics, we need to account for the fact that light behaves in some respects like a classical wave and in other respects like a classical particle. It is not a mere coincidence that Einstein wrote his seminal paper on light quanta almost simultaneously with his paper on the electrodynamics of moving bodies. He could legitimately have combined the two into a single paper, discussing general heuristic considerations arising from the observed properties of light, reconciling what would classically seem to be the irreconcilable wave-like and particle-like attributes. |
|
|
|
In §10 of the paper, Einstein derives expressions for the so-called longitudinal and transverse masses (albeit with force and acceleration defined in terms of different coordinate systems), terms that had been used previously by, e.g., Abraham and Lorentz. These expressions show (in primitive form, for kinetic energy) the inertia of energy, an equivalence that was to be further elaborated by Einstein in a brief follow-up paper in September of 1905. Although the expressions were not new, the understanding of their significance was new. Lorentz had derived the longitudinal and transverse masses in §9 of his 1904 paper from purely electrodynamical considerations (the effect of self-induction), and then commented that these represent the electromagnetic masses of the electron. He went on to say |
|
|
|
I shall suppose that there is no other, no “true” or “material” mass. |
|
|
|
Poincare and other authors had said much the same. Surprisingly, even as late as 1908 we find Minkowski saying at the conclusion of his famous paper on spacetime that “The validity without exception of the world-postulate is the true nucleus of an electromagnetic image of the world…”. In contrast, after giving his own derivation of these expressions, Einstein first cautions that they depend somewhat on the definition of force (anticipating Planck’s later re-working of the foundations of relativistic mechanics), and then writes one of the most important sentences in the paper: |
|
|
|
It should be noted that these results concerning mass are also valid for ponderable material points, since a ponderable material point can be made into an electron (in our sense) by adding to it an arbitrarily small electric charge. |
|
|
|
Thus, unlike his predecessors, Einstein has clearly grasped that these relations for the effective inertia, dependent on speed, apply not just to the so-called electromagnetic mass arising from self-induction, but to mass in general. (See Section 2.3 for derivation of these expressions purely from the relation between inertial coordinate systems, without reference to electrodynamics.) This is one of the clearest examples of how Einstein’s special relativity transcends its origins in Maxwell’s equations to become a fundamental theory of the inertia-based measures of space and time, applicable to mechanics (and any other forces) as well as electromagnetism. |
|
|
|
Although Einstein didn’t explicitly address the inertia of all forms of energy until the September 1905 paper, the June paper included an important precursor by deriving in §10 the fact that the kinetic energy of a particle of (rest) mass m moving at speed v in terms of any given system of inertial coordinates is |
|
|
|
|
|
|
|
This clearly suggests that the first term on the right side represents the total energy, and the second term represents the “rest energy” of the mass m, the difference between them being the kinetic energy. He repeats that this applies not just to electrically charged particles, but to all ponderable mass. Consistent with this, in the September paper Einstein showed that "radiation carries inertia between emitting and absorbing bodies". In other words, light conveys not only momentum, but inertia. For example, after a body has absorbed an elementary pulse of light, it has not only received a “kick” from the momentum of the light, but the internal inertia (i.e., the inertial mass) of the body has actually increased. |
|
|
|
It might seem that Einstein’s second principle is implied by the first, at least if Maxwell's equations are regarded as laws governing the changes of physical systems, because Maxwell's equations prescribe the speed of light propagation independent of the source's motion. Indeed, Einstein alluded to this very point at the beginning of his September 1905 paper. However, it’s not clear a priori whether Maxwell’s equations are valid in terms of relatively moving systems of coordinates, nor whether the permissivity of the vacuum is independent of the frame of reference in terms of which it is evaluated. Moreover, by 1905 Einstein already doubted the absolute validity of Maxwell's equations, having recently completed his paper on the photo-electric effect which introduced the idea of photons, i.e., light propagating as discrete packets of energy, a concept which cannot be represented as a solution of Maxwell's linear equations. |
|
|
|
Einstein also realized that a purely electromagnetic theory of matter based on Maxwell's linear equations was impossible, because those equations by themselves could never explain the stable equilibria of the electrically charged particles that comprise atoms. He believed that "only different, nonlinear field equations could possibly accomplish such a thing." This observation shows how unjustified was the "molecular force hypothesis" of Lorentz, according to which all the forces of nature were assumed to transform exactly as do electromagnetic forces as described by Maxwell's linear equations. |
|
|
|
Knowing that the forces responsible for the equilibrium of charged particles and atoms must necessarily be of a fundamentally different character than the forces of electromagnetism in the classical sense, and that the stability of matter may not even have a description in the form of a classical field theory at all, it's clear that Lorentz's hypothesis has no constructive basis, and is simply tantamount to the adoption of some set of principles that entail Lorentz invariance. Instead of basing special relativity on an assumption of the absolute validity of Maxwell's equations, Einstein based it on the particular characteristic exhibited by those equations, namely Lorentz invariance, that he intuited was the more fundamental principle, one that could serve as an organizing principle analogous to the conservation of energy in thermodynamics, and one that could encompass all physical laws, even if they turned out to be completely dissimilar to Maxwell's equations. Remarkably, this has turned out to be the case. Lorentz invariance is a key aspect of the modern theory of quantum electrodynamics, which replaced Maxwell’s equations. |
|
|
|
Although Einstein explicitly highlighted just two principles as the basis of special relativity in his 1905 paper (consciously patterned after the two principles of thermodynamics), his derivation of the Lorentz transformation also invoked what he called “the properties of homogeneity that we attribute to space and time” to establish the linearity of the transformations. (Linear fractional transformations are ruled out by stipulating continuity of the coordinates of a particle, or simply by requiring that finite coordinates map to finite coordinates.) In addition, he tacitly assumed spatial isotropy, i.e., that there is no preferred direction in space, so the intrinsic properties of ideal rods and clocks do not depend on their spatial orientations. Lastly, as mentioned above, he assumed memorylessness, i.e., that the extrinsic properties of rods and clocks (or atoms) may be functions of their current positions and states of motion but not their previous positions or states of motion. This last assumption is needed to exclude the possibility that every elementary particle may somehow "remember" its entire history of accelerations, and thereby "know" its present absolute velocity relative to a common fixed reference. Einstein explicitly listed these extra assumptions in an exposition written in 1920. He may have gained an appreciation of the importance of the independence of measuring rods and clocks from their past history after considering Weyl’s unified field theory, which Einstein rejected precisely because it violated this premise. |
|
|
|
The principles that Einstein chose in June 1905 as the basis of his deductions were not the only ones possible. In particular, although the principle of relativity itself is fairly unobjectionable (and not novel), he could have chosen a different “second” principle. “Postulating” the invariance of the speed of light (in vacuum) in terms of relatively moving systems of inertia-based coordinates (which is essentially what he did by the combination of his two principles) is almost guaranteed to elicit skepticism, if not outright disbelief, because it is logically incompatible with the reader’s (at that point) unchallenged assumption that inertial coordinates are related by Galilean transformations. In the following section we discuss some alternative approaches to logically deducing special relativity from the most manifest set of basic principles. |
|
|