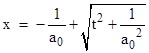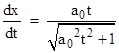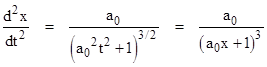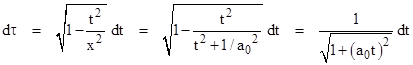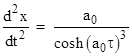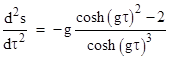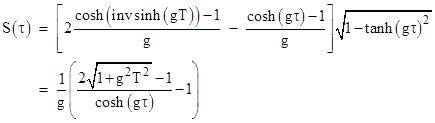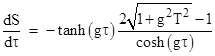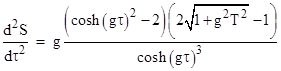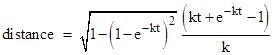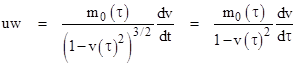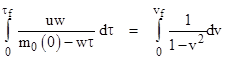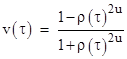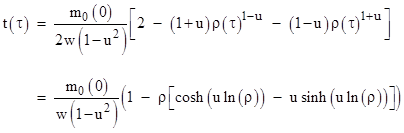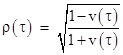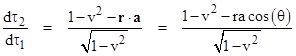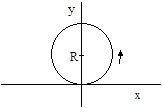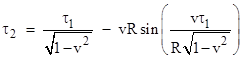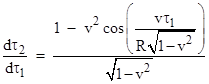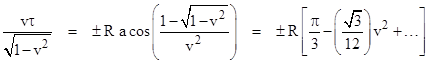2.9  Accelerated Travels

This yields the following peculiar consequence: If there are two synchronous clocks, and one of them is moved along a closed curve with constant [speed] until it has returned, then this clock will lag on its arrival behind the clock that has not been moved.

                                                                  Albert Einstein, 1905

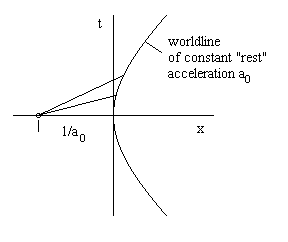
Suppose a particle accelerates in such a way that it is subjected to a constant proper acceleration a₀ for some period of time. The proper acceleration of a particle is defined as the acceleration with respect to the particle's momentarily co-moving inertial coordinate system at any given instant. The particle's velocity is v = 0 at the time t = 0, when it is located at x = 0, and at some infinitesimal time Δt later its velocity is Δt a₀ and its location is (1/2) a₀ Δt². Using units such that c=1, the slope of its line of simultaneity is the inverse of the slope 1/v of its worldline, so its locus of simultaneity at t = Δt is the line given by

This line intersects the particle's original locus of simultaneity at the fulcrum event (x_f,0) where

At each instant the particle is similarly accelerating relative to its current instantaneous rest frame, so in the continuous limit its inertial locus of simultaneity constantly passes through the event (−1/a₀, 0) in terms of its co-moving inertial coordinate system, and hence the particle maintains a constant absolute spacelike distance of −1/a₀ from that point, as illustrated in the figure below.

The fulcrum event is the center of the two-branched hyperbola. The coordinate equation for this worldline is

The derivative with respect to t gives the coordinate velocity

which asymptotically approaches 1, and the second derivative gives the coordinate acceleration

which asymptotically approaches zero. Since the worldline of a particle with constant proper acceleration is a branch of a hyperbola with "radius" 1/a₀, we can shift the x axis by 1/a₀ to place the origin at the center of the hyperbola, and then write the equation of the worldline as

Differentiating both sides with respect to t gives

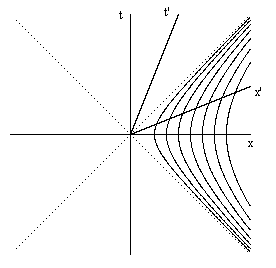
which shows that the velocity of the worldline at any point (x,t) is given by v = t/x. Consequently the line from the origin through any point on the hyperbolic path represents the space axis for the co-moving inertial coordinates of the accelerating worldline at that point. (We will refer to distances from any point on a time-like path in terms of the co-moving inertial coordinates as frame distances.) The same applies to any other hyperbolic path asymptotic to the same lightlines, so a line from the origin intersects any two such hyperbolas at points that are mutually simultaneous and separated by a constant frame distance (since they are both a fixed frame distance from the origin along their mutual space axis). It follows that in order for a slender "rigid" rod accelerating along its axis to maintain a constant frame length (with respect to its co-moving inertial frames), the parts of the rod must accelerate along a family of hyperbolas asymptotic to the same lightlines, as illustrated below.

The x′,t′ axes represent the mutual co-moving inertial frame of the hyperbolic worldlines where they intersect with the x′ axis. All the worldlines have constant frame distances from each other along this axis, and all have the same speed. The latter implies that they have each been accelerated by the same total amount at any instant of their mutual co-moving inertial frame, but the accelerations have been distributed differently. The "inner-most" worldline (i.e., the trailing end of the rod) has been subjected to a higher level of instantaneous acceleration but for a shorter time, whereas the "outer-most" worldline (i.e., the leading end of the rod) has been accelerated more mildly, but for a longer time. It's worth noting that this form of "coherent" acceleration would not occur if the rod were accelerated simply by pushing on one end. It would require the precisely coordinated application of distinct force profiles to each individual particle of the rod. Any deviation from these profiles would result in internal stresses of one part of the rod on another, and hence the rest length would not remain fixed. Furthermore, even if the coherent acceleration profiles are perfectly applied, there is still a sense in which the rod has not remained in complete physical equilibrium, because the elapsed proper times along the different hyperbolic worldlines as the rod is accelerated from a rest state in x,t to a rest state in some x′,t′ differ, and hence the quantum phases of the two ends of the rod are shifted with respect to each other. Thus we must assume memorylessness (as mentioned in Section 1.6) in order to assert the equivalence of the equilibrium states for two different frames of reference.

We can then determine the lapse of proper time τ along any given hyperbolic worldline using the relation, which leads (for the hyperbola of unit "radius") to

Integrating this relation gives

Solving this for t and substituting into the equation of the hyperbola to give x, we have the parametric equation of the hyperbola as a function of the proper time along the worldline. If we subtract 1/a₀ from x to return to our original x coordinate (such that x = 0 at t = 0) these equations are

Differentiating the above expressions gives

so the particle's velocity relative to the original inertial coordinates is

Differentiating again with respect to t gives the coordinate acceleration

in agreement with the expressions derived previously. We're using "time units" throughout this section, which means that all times and distances are expressed in units of time. For example, if the proper acceleration of the particle is 1g (the acceleration of gravity at the Earth's surface), then

g    =    (3.27)10^-8  sec⁻¹    =   1.031  years⁻¹

and all distances are in units of light-seconds.

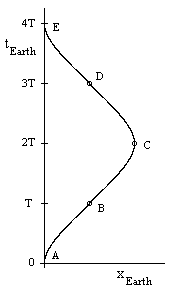
To show the implications of these formulas, suppose a space traveler moves away from the Earth with a constant proper acceleration of 1g for a period of T years as measured on Earth. He then reverses his acceleration, coming to rest after another T years has passed on Earth, and then continues his constant Earthward acceleration for another T Earth-years, at which point he reverses his acceleration again and comes to rest back at the Earth in another T Earth-years. The total journey is completed in 4T Earth-years, and it consists of 4 similar hyperbolic segments as illustrated below.

There are several questions we might ask about this journey. First, how far away from Earth does the traveler reach at his furthest point? This occurs at point C, which is at 2T according to Earth time, when the traveler's acceleration brings him momentarily to rest with respect to the Earth. To answer this question, recall that τ can be expressed as a function of t by

Now, the maximum distance from Earth is twice the distance at point B, when t = T, so we have

The maximum speed of the traveler in terms of the Earth's inertial coordinates occurs at point B, where t = T (and again at point D, where t = 3T), and so is given by

The total elapsed proper time for the traveler during the entire journey out and back, which takes 4T years according to Earth time, is 4 times the lapse of proper time to point B at t = T, so it is given by

So far we have focused mainly on a description of events in terms of the Earth's inertial coordinates x and t, but we can also describe the same events in terms of coordinate systems associated with the accelerating traveler. At any given instant the traveler is momentarily at rest with respect to a system of inertial coordinates, so (as above) we can define "frame" time and space measurements in terms of these coordinates. However, when we differentiate these time and space intervals as the traveler progresses along his worldline, we will find that new effects appear, due to the fact that the coordinate system itself is changing. As the traveler accelerates he continuously progresses from one system of momentarily co-moving inertial coordinates to another, and the effect of this change in the coordinates will show up in any derivatives that we take with respect to the time and space components.

For example, suppose we ask how fast the Earth is moving relative to the traveler. This question can be interpreted in different ways. With respect to the traveler's momentarily co-moving inertial coordinates, the Earth's velocity is equal and opposite to the traveler's velocity with respect to the Earth's inertial coordinates. However, this quantity does not equal the derivative of the frame distance with respect to the proper time. The frame distance s from the Earth in terms of the traveler's momentarily co-moving inertial coordinates at the proper time τ is

which shows that the frame distance approaches a constant 1/g (about 1 light-year) as τ increases. This shouldn't be surprising, because we've already seen that the traveler's frame distance from a fixed point on the other side of the Earth actually is constant and equal to 1/g throughout the period of constant proper acceleration.

The derivative of the frame distance of the Earth with respect to the proper time is

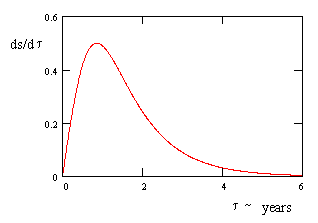
This can be regarded as a kind of velocity, since it represents the proper rate of change of the frame distance from the Earth as the traveler accelerates away. A plot of this function as τ varies from 0 to 6 years is shown below.

Initially the frame distance from the Earth increases as the traveler accelerates away, but eventually (if the constant proper acceleration is maintained for a sufficiently long time) the "length contraction" effect of his increasing velocity becomes great enough to cause the derivative to drop off to zero as the frame distance approaches a constant 1/g. To find the point of maximum ds/dτ we differentiate again with respect to τ to give

Setting this to zero, we see that the maximum occurs at t = invcosh(√2)/g, and substituting this into the expression for ds/dτ gives the maximum value of 1/2. Thus the derivative of frame distance from Earth with respect to proper time during a constant 1g acceleration away from the Earth reaches a maximum of half the speed of light at a proper time of about 0.856 years, after which it drops to zero.

Similarly, the traveler's frame distance S from the turnaround point is given by

The derivative of this with respect to the traveler's proper time is

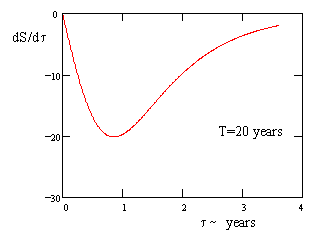
A plot of this "velocity" is shown below for the first quartile leg of a journey as described above with T = 20 years.

The magnitude of this "velocity" increases rapidly at the start of the acceleration, due to the combined effects of the traveler's motion and the onset of "length contraction", but if allowed to continue long enough the "velocity" drops off and approaches 2 (i.e., twice the speed of light) at the point where the traveler reverses his acceleration. Of course, the fact that this derivative exceeds c does not conflict with the fact that c is an upper limit on velocities with respect to inertial coordinate systems, because S and τ do not constitute inertial coordinates.

To find the extreme point on this curve we differentiate again with respect to τ, which gives

Consequently the extreme value occurs (assuming the journey is long enough and the acceleration is great enough) at the proper time τ = invcosh(√2)/g, where the value of dS/dτ is

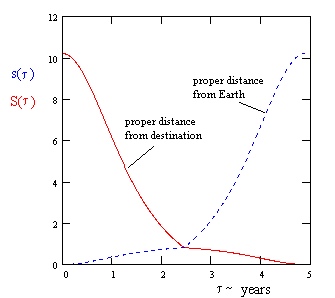
By symmetry, these same two characteristics apply to all four of the "quadrants" of the traveler's journey, with the appropriate changes of sign and direction. The figure below shows the frame distances s(t) and S(t) (i.e., the distances from the origin and the destination respectively) during the first two quadrants of a journey with T = 6.

Also by symmetry, the portions of these curves to the right of the mid-point can be generated from the relation s(τ) = S(τ_C − τ). Also, it's obvious that

If we consider journeys with non-constant proper accelerations, it's possible to construct some slightly peculiar-sounding scenarios. For example, suppose the traveler accelerates in such a way that his velocity is 1 − exp(−kt) for some constant k. It follows that the distance in the Earth's frame at time t is [kt + exp(−kt) − 1]/k, so the distance in the traveler's frame is

This function initially increases, then reaches a maximum, and then asymptotically approaches zero. With k = 1 year⁻¹ the maximum occurs at roughly 3 years and a distance of about 0.65 light-years (relative to the traveler's frame). Thus we have the seemingly paradoxical situation that the Earth "becomes closer" to the traveler as he moves further away.

This is not as strange as it may sound at first. Suppose we leave home and drive for 1 hour at a constant speed of 20 mph. We could then say that we are "1 hour from home". Now suppose we suddenly accelerate to 40 mph. How far (in time) are we away from home? If we extrapolate our current worldline back in time, we are only 1/2 hour from home. If we speed up some more, our "distance" (in terms of time) from home becomes less and less, provided we speed up at a rate that more than compensates for the increasing road distance, but that's not hard to do (in theory). The only difference between this scenario and the relativistic one is that when we accelerate to relativistic speeds both our time and our space axes are affected, so when we extrapolate our current frame of reference back to Earth we find that both the time and the distance are shortened.

Another interesting acceleration profile is the one that results from a constant nozzle velocity u and constant exhaust mass flow rate w = dm₀/dτ, where τ is the proper time of the rocket. The effective force is uw throughout the acceleration, but this does not result in constant proper acceleration, because the rest mass of the rocket is being reduced while the applied proper force remains constant. In this case we have

where t is the time of the initial coordinates and v is the velocity of the rocket with respect to those coordinates. Also, we have m₀(τ) = m₀(0) − wτ, so we can integrate to get the speed

Letting ρ(τ) denote the ratio [m₀(0) − wτ]/m₀(0), which is the ratio of rest masses at the start of the acceleration to the rest mass at proper time τ, the result is

so we have

Also, since dt = dτ /, we can integrate this to get the coordinate time t as a function of the rocket's proper time

In the limit as the nozzle velocity u approaches 1, this expression reduces to

It's interesting that for photonic propulsion (u=1) the mass ratio ρ is identical to the Doppler frequency shift of the exhaust photons relative to the original rest frame, i.e., we have

Thus if the rocket continues to convert its own mass to energy and eject it as photons of a fixed frequency, the energy of each photon as seen from the fixed point of origin is exactly proportional to the rest mass of the rocket at the moment when the photon was ejected. Also, since r(t) is the current rest mass m₀(t) divided by the original rest mass m₀(0), and since the inertial mass m(t) is related to the rest mass m₀(t) by the equation m(t) = m₀(t) /, we find that the inertial mass m(t) of the rocket is given as a function of the rocket's velocity v by the equation

Hence, as the rocket's velocity goes to 1 at the moment when it is converting the last of its rest mass into energy (so its rest mass is going to zero), its inertial mass goes to m₀(0)/2, i.e., exactly half of the rocket's original rest mass. This is to be expected, because momentum must be conserved, and all the photons except the very last have been ejected in the rearward direction at the speed of light, leaving only the last remaining photon (which has nothing to react against) moving in the forward direction, so it must have momentum equal to all the rearward momentum of the ejected photons. The momentum of a photon is p = hν/c = E/c, so in units with c = 1 we have p = E. The original energy content of the rocket was it's rest mass, m₀(0), which has been entirely converted to energy, half in the forward direction (in the last remaining super-energetic photon) and half in the rearward direction (the progressively more redshifted stream of exhaust photons).

The preceding discussion focused on purely linear motion, but we can just as well consider arbitrary accelerated paths. It's trivial to determine the lapse of proper time along any given timelike path as a function of an inertial time coordinate simply by integrating dt over the path, but it's a bit more challenging to express the lapse of proper time along one arbitrary worldline with respect to the lapse of proper time along another, because the appropriate correspondence is ambiguous. One obvious correspondence is given by mapping the proper time along the reference worldline to the proper time along the subject worldline by means of the instantaneously co-moving planes of inertial simultaneity of the reference worldline. In other words, to each point along the reference worldline we can assign a locus of simultaneous points based on co-moving inertial coordinates at that point, and we can then find the intersections of these loci with the subject worldline.

Quantitatively, suppose the reference worldline W₁ is given parametrically by the functions x₁(t), y₁(t), z₁(t) where x,y,z,t are inertial coordinates. From this we can determine the derivatives = dx₁/dt,  = dy₁/dt, and  = dz₁/dt. These also represent the components of the gradient of the space of simultaneity of the instantaneously co-moving inertial frame of the object. In other words, the spaces of simultaneity for W₁ have the partial derivatives

These enable us to express the total differential time as a function of the differentials of the spatial coordinates

If the subject worldline W₂ is expressed parametrically by the functions x₂(t), y₂(t), z₂(t), and if the inertial plane of simultaneity of the event at coordinate time t₁ on W₁ is intersected by W₂ at the coordinate time t₂, then the difference in coordinate times between these two events can be expressed in terms of the differences in their spatial coordinates by substituting into the above total differential the quantities dt = t₂−t₁, dx = x₂(t₂)−x₁(t₁) and so on. The result is

where the derivatives of x₁, y₁, and z₁ are evaluated at t₁. Rearranging terms and omitting the indications of functional dependence for the W₁ coordinates, this can be written in the form

This is an implicit formula for the value of t₂ on W₂ corresponding to t₁ on W₁ based on the instantaneous inertial simultaneity of W₁. Every quantity in this equation is an explicit function of either t₁ or t₂, so we can solve for t₂ to give a function F₁ such that t₂ = F₁(t₁). We can also integrate the absolute intervals along the two worldlines to give the functions f₁ and f₂ which relate the proper times along W₁ and W₂ to the coordinate time, i.e., we have τ₁ = f₁(t) and τ₂ = f₂(t). With these substitutions we arrive at the general form of the expression for τ₂ with respect to τ₁:

To illustrate, suppose W₁ is the worldline of a particle moving along some arbitrary path and W₂ is just the worldline of the spatial origin of the inertial coordinates. In this case we have x₂ = y₂ = z₂ = 0 and τ₂ = t₂, so the above formula reduces to

where r and v are the position and velocity vectors of W₁ with respect to the inertial rest coordinates of W₂. Differentiating with respect to t₁, and multiplying through by dt₁/dt₁ = (1−v²)^−1/2, we get

where a is the acceleration vector and θ is the angle between the r and a vectors. Thus if the acceleration of W₁ is zero, we have dτ₂/dτ₁ = (1−v²)^1/2. On the other hand, if W₁ is moving around W₂ in a circle at constant speed, we have a = –v²/r and the position and acceleration vectors are anti-parallel, giving the result dτ₂/dτ₁ = (1−v²)^−1/2. This is consistent with the fact that, if the object is moving tangentially, the plane of simultaneity for its instantaneously co-moving inertial coordinate system intersects with the constant-t plane along the line from the object to the origin, and hence the time difference is entirely due to the transverse dilation (i.e., the square root of 1−v² factor).

If the speed v of W₁ is constant, then we have the explicit equation

To illustrate, suppose the object whose worldline is W₁ begins at the origin at t = 0 and thereafter moves counter-clockwise in a circle tangent to the origin in the xy plane with a constant angular velocity ω as illustrated below.

In this case the object's spatial coordinates and their derivatives as a function of coordinate time are

Substituting into the equation for τ₂ and replacing each appearance of t with  gives the result

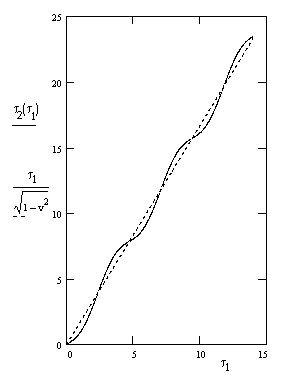
This is the proper time of the spatial origin according to the instantaneous time slices of the moving object's proper time. This function is plotted below with R = 1 and v = 0.8. Also shown is the stable component .

Naturally if the circle radius R goes to infinity the value of the sine function approaches the argument, and so the above expression reduces to

This confirms the reciprocity between the two worldlines when both are inertial. We can also differentiate the full expression for τ₂ as a function of τ₁ to give the relation between the differentials

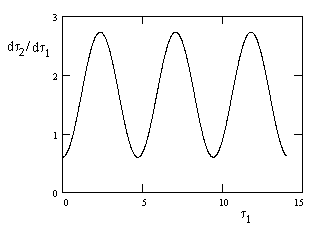
This relation is plotted in the figure below, again for R = 1 and v = 0.8.

It's also clear from this expression that as R goes to infinity the cosine approaches 1, and we again have .

Incidentally, the above equation shows that the ratio of time rates equals 1 when the moving object is a circumferential distance of

from the point of tangency. Hence, for small velocities v the configuration of "equal time rates" occurs when the moving object is at ±π/3 radians from the point of tangency. On the other hand, as v approaches 1, the configuration of equal time rates occurs when the moving object approaches the point of tangency. This may seem surprising at first, because we might expect the proper time of the origin to be dilated with respect to the proper time of the tangentially moving object. However, the planes of simultaneity of the moving object are tilting very rapidly in this condition, and this offsets the usual time dilation factor. As v approaches 1, these two effects approach equal magnitude, and cancel out for a location approaching the point of tangency.

Return to Table of Contents