|
2.10
The Starry Messenger
|
|
|
|
“Let God look
and judge!”
|
|
Cardinal Humbert, 1054 AD
|
|
|
|
Maxwell's
equations are very successful at describing the propagation of light based on
the model of electromagnetic waves, not only in material media but also in a
vacuum, which is considered to be a region free of material substances.
According to this model, light propagates in vacuum at a speed 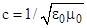 , where μ0 is the
permeability constant and ε0 is the permittivity of the
vacuum, defined in terms of Coulombs law for electrostatic force , where μ0 is the
permeability constant and ε0 is the permittivity of the
vacuum, defined in terms of Coulombs law for electrostatic force
|
|
|
|
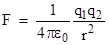
|
|
|
|
The
SI system of units is defined so that the permeability constant takes on the
value μ0 = 4π10−7 tesla meter per
ampere, and we can measure the value of the permittivity (typically by
measuring the capacitance C between parallel plates of area A separated by a
distance d, using the relation ε0 = Cd/A) to have the value ε0
= (8.854187818)10−12 coulombs2 per newton meters2.
This leads to the familiar value
|
|
|
|
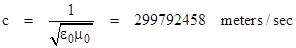
|
|
|
|
for
the speed of light in a vacuum. Of course, if we place some substance between
our capacitors when determining ε0 we will generally get a
different value, so the speed of light is different in various media. This
leads to the index of refraction of various transparent media, defined as n =
cvacuum / cmedium. Thus Maxwell's theory of
electro-magnetism seems to clearly imply that the speed of propagation of
such electromagnetic waves depends only on the medium, and is independent of
the speed of the source.
|
|
|
|
On
the other hand, it also suggests that the speed of light depends on the
motion of the medium, which is easy to imagine in the case of a material
medium like glass, but not so easy if the "medium" is the vacuum of
empty space. How can we even assign a state of motion to the vacuum? In
struggling to answer this question, people tried to imagine that even the
vacuum is permeated with some material-like substance, the ether, to which a
definite state of motion could be assigned. On this basis it was natural to
suppose that Maxwell's equations were strictly applicable (and the speed of
light was exactly c) only with respect to the absolute rest frame of
the ether. With respect to other frames of reference they expected to find
that the speed of light differed, depending on the direction of travel.
Likewise we would expect to find corresponding differences and anisotropies
in the capacitance of the vacuum when measured with plates moving at high
speed relative to the ether.
|
|
|
|
However,
when extremely precise interferometer measurements were carried out to find a
directional variation in the speed of light on the Earth's surface
(presumably moving through the ether at fairly high speed due to the Earth's
orbital motion around the Sun), essentially no directional variation in light
speed was found that could be attributed to the motion of the apparatus
through the ether. Naturally it had occurred to people that the ether might
be "dragged along" by the Earth, so that objects on the Earth's
surface are essentially at rest in the local ether. However, these
"convection" hypotheses are inconsistent with other observed
phenomena, notably the aberration of starlight, which can only be explained
in an ether theory if it is assumed that an observer on the Earth's surface is
not at rest with respect to the local ether. Also, careful terrestrial
measurements of the paths of light near rapidly moving massive objects showed
no sign of any "convection". Considering all this, the situation
was considered to be quite puzzling.
|
|
|
|
There
is a completely different approach that could be taken to modeling the
phenomena of light, provided we're willing to reject Maxwell's theory of
electromagnetic waves, and adopt instead a model similar to the one that
Newton often seemed to have in mind, namely, an "emission theory".
One advocate of such a theory in the early 1900's was Walter Ritz, who
rejected Maxwell's equations on the grounds that the advanced potentials
allowed by those equations were unrealistic. Ritz debated this point with
Albert Einstein, who argued that the observed asymmetry between advanced and
retarded waves is essentially statistical in origin, due to the improbability
of conditions needed to produce coherent advanced waves. Neither man
persuaded the other. (Ironically, Einstein himself had already posited that
Maxwell's equations were inadequate to fully represent the behavior of light,
and suggested a model that contains certain attributes of an emission theory
to account for the photo-electric effect, but this challenge to Maxwell's
equations was on a more subtle and profound level than Ritz's objection to
advanced potentials.)
|
|
|
|
In
place of Maxwell's equations and the electromagnetic wave model of light, the
advocates of "emission theories" generally assume a Galilean or Newtonian
spacetime, and postulate that light is emitted and propagates away from the
source (perhaps like Newtonian corpuscles) at a speed of c relative to the
source. Thus, according to emission theories, if the source is moving
directly toward or away from us with a speed v, then the light from that
source is approaching us with a speed c+v or c−v respectively.
Naturally this class of theories is compatible with experiments such as the
one performed by Michelson and Morley, since the source of the light is
moving along with the rest of the apparatus, so we wouldn't expect to find
any directional variation in the speed of light in such experiments. Also, an
emission theory of light is compatible with stellar aberration, at least up
to the limits of observational resolution. In fact, James Bradley (the
discoverer of aberration) originally explained it on this very basis.
|
|
|
|
Of
course, even an emission theory must account for the variations in light
speed in different media, which means it can't simply say that the speed of
light depends only on the speed of the source. It must also be
dependent on the medium through which it is traveling, and presumably it must
have a "terminal velocity" in each medium, i.e., a certain
characteristic speed that it can maintain indefinitely as it propagates
through the medium. (Obviously we never see light come to rest, nor even do
we observe noticeable "slowing" of light in a given medium, so it
must always exhibit a characteristic speed.) Furthermore, based on the principles
of an emission theory, the medium-dependent speed must be defined relative to
the rest frame of the medium.
|
|
|
|
For
example, if the characteristic speed of light in water is cw, and
a body of water is moving relative to us with a speed v, then (according to
an emission theory) the light must move with a speed cw + v
relative to us when it travels for some significant distance through that
water, so that it has reached its "steady-state" speed in the
water. In optics this distance is called the "extinction distance",
and it is known to be proportional to 1/(ρλ), where ρ is the
density of the medium and λ is the wavelength of light. The extinction
distance for most common media for optical light is extremely small, so
essentially the light reaches its steady-state speed as soon as it enters the
medium.
|
|
|
|
An
experiment performed by Fizeau in 1851 to test for optical
"convection" also sheds light on the viability of emission
theories. Fizeau sent beams of light in both directions through a pipe of
rapidly moving water to determine if the light was "dragged along"
by the water. Since the refractive index of water is about n = c/cw
= 1.33 where cw is the speed of light in water, we know that cw
equals c/1.33, which is about 75% of the speed of light in a vacuum. The
question is, if the water is in motion relative to us, what is the speed
(relative to us) of the light in the water?
|
|
|
|
If
light propagates in an absolutely fixed background ether, and isn't dragged
along by the water at all, we would expect the light speed to still be cw
relative to the fixed ether, regardless of how the water moves. This is
admittedly a rather odd hypothesis (i.e., that light has a characteristic
speed in water, but that this speed is relative to a fixed background ether,
independent of the speed of the water), but it is one possibility that can't
be ruled out a priori. In this case the difference in travel times for
the two directions would be proportional to
|
|
|
|
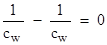
|
|
|
|
which
implies no phase shift in the interferometer. On the other hand, in an
emission theory with extinction (or, equivalently, in an ether theory with
complete convection), the speed of the light in the water (which is moving at
the speed v) should be cw+v in the direction of the water's
motion, and cw−v in the opposite direction. On this basis
the difference in travel times would be proportional to
|
|
|
|
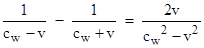
|
|
|
|
This
is a very small amount (remembering that cw is about 75% of the
speed of light in a vacuum), but it is large enough that it would be
measurable with delicate interferometry techniques.
|
|
|
|
The
results of Fizeau's experiment turned out to be consistent with neither
of the above predictions. Instead, he found that the time difference
(proportional to the phase shift) was a bit less than 43.5% of the prediction
for an emission theory (or a totally dragged ether theory), i.e., 43.5% of
the prediction based on the assumption of complete convection. This result
was in accord with the partially dragged ether hypothesis put forward by
Fresnel, as discussed in Section 2.5. By varying the density of the fluid we
can vary the refractive index and therefore cw, and we find that
the measured phase shift always indicates a time difference of (1−cw2)
times the prediction of the emission theory. For water we have cw
= 0.7518, so the time lag is (1−cw2) = 0.4346 of
the prediction of an emission theory (or of an ether theory with complete
convection) and Galilean kinematics.
|
|
|
|
This
implies that if we let S(cw,v) and S(cw,−v)
denote the speeds of light in the two directions, we have
|
|
|
|
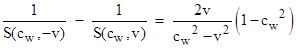
|
|
|
|
By
partial fraction decomposition this can be written in the form
|
|
|
|
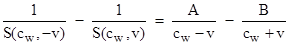
|
|
|
|
where
|
|
|
|
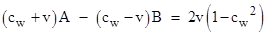
|
|
|
|
Also,
in view of the symmetry S(u,v) = S(v,u), we can swap cw with v to
give
|
|
|
|
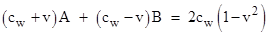
|
|
|
|
Solving
these last two equations for A and B gives A = 1 − vcw and B
= 1 + vcw, so the function S is
|
|
|
|
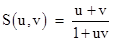
|
|
|
|
which
of course is the relativistic formula for the composition of velocities. So,
even if we rejected Maxwell's equations, it still appears that emission
theories (and fully dragged ether theories) can’t be reconciled with Fizeau's
experimental results.
|
|
|
|
More
evidence ruling out simple emission theories comes from observations of a
supernova made by Chinese astronomers in the year 1054 AD. When a star
explodes as a supernova, the initial shock wave moves outward through the
star's interior in just seconds, and elevates the temperature of the material
to such a high level that fusion is initiated, and much of the lighter
elements are fused into heavier elements, including some even heavier than
iron. (This process yields most of the interesting elements that we find in
the world around us.) Material is flung out at high speeds in all directions,
and this material emits enormous amounts of radiation over a wide range of
frequencies, including x-rays and gamma rays. Based on the broad range of
spectral shifts (resulting from the Doppler effect), it's clear that the
sources of this radiation have a range of speeds relative to the Earth of
over 10000 km/sec. This is because we are receiving light emitted by some
material that was flung out from the supernova in the direction away from the
Earth, and by other material that was flung out in the direction toward the
Earth.
|
|
|
|
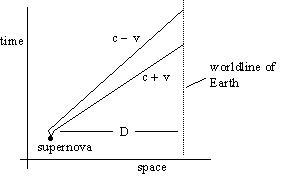
If
the supernova was located a distance D from us, then the time for the
"light" (i.e., EM radiation of all frequencies) to reach us should
be roughly D/c, where c is the speed of light. However, if we postulate that
the actual speed of the light as it travels through interstellar space is
affected by the speed of the source, and if the source was moving with a
speed v relative to the Earth at the time of emission, then we would conclude
that the light traveled at a speed of c+v on it's journey to the Earth.
Therefore, if the sources of light have velocities ranging from −v to
+v, the first light from the initial explosion to reach the Earth would
arrive at the time D/(c+v), whereas the last light from the initial explosion
to reach the Earth would arrive at the time D/(c−v) as depicted in the
figure below.
|
|
|
|
|
|
|
|
Consequently
the arrival times for light from the initial explosion event would be spread
out over an interval of length D/(c−v) − D/(c+v), which equals
(D/c)(2v/c) / (1−(v/c)2). The denominator is virtually 1, so
we can say the interval of arrival times for the light from the explosion
event of a supernova at a distance D is about (D/c)(2v/c), where v is the
maximum speed at which radiating material is flung out from the supernova.
|
|
|
|
However,
in actual observations of supernovae we do not see this
"spreading out" of the event. For example, the Crab supernova was
about 6000 light years away, so we had D/c = 6000 years, and with a range of
source speeds of 10000 km/sec (meaning v = ±5000) we would expect a range of
arrival times of 200 years, whereas in fact the Crab was only bright for less
than a year, according to the observations recorded by Chinese astronomers in
July of 1054 AD. For a few weeks the "guest star", as they called
it, in the constellation Taurus was the brightest star in the sky, and was
even visible in the daytime for twenty-six days. Within two years it had
disappeared completely to the naked eye. (It was not visible in Europe or the
Islamic countries, since Taurus is below the horizon of the night sky in July
for northern latitudes.) In the time since the star went supernova the debris
has expanded to it's present dimensions of about 3 light years, which implies
that this material was moving at only (!) about 1/300 the speed of light.
Still, even with this value of v, the bright explosion event should have been
visible on Earth for about 40 years (if the light really moved through space
at c ± v). Since it was actually visible for only a small fraction of this
time, we can conclude that the light actually propagated through space at a
speed essentially independent of the speed of the sources.
|
|
|
|
This
source independence of light speed is obviously consistent with Maxwell's
equations and special relativity, but we should be careful not to read too
much into it. In particular, this isn't direct proof that the speed of light
in a vacuum is independent of the speed of the source, because for visible
light (which is all that was noted on Earth in July of 1054 AD) the
extinction distance in the gas and dust of interstellar space is much less
than the 6000 light year distance of the Crab nebula. In other words, for
visible light, interstellar space is not a vacuum, at least not over
distances of many light years. Hence it's possible to argue that even if the
initial speed of light in a vacuum was c+v, it would have slowed to c for
most of its journey to Earth. Admittedly, the details of such a counter-factual
argument are lacking (because we don't really know the laws of propagation of
light in a universe where the speed of light is dependent on the speed of the
source, nor how the frequency and wavelength would be altered by interaction
with a medium, so we don't know if the extinction distance is even relevant),
but it's not totally implausible that the static interstellar dust might
affect the propagation of light in such a way as to obscure the source
dependence, and the extinction distance seems a reasonable way of quantifying
this potential effect.
|
|
|
|
A
better test of the source-independence of light speed based on astronomical
observations is to use light from the high-energy end of the spectrum. As
noted above, the extinction distance is proportional to 1/(ρλ). For
some frequencies of x-rays and gamma rays the extinction distance in
interstellar space is about 60000 light years, much greater than the
distances to many supernova events, as well as binary stars and other
configurations with identifiable properties. By observing these events and
objects it has been found that the arrival times of light are essentially
independent of frequency, e.g., the x-rays associated with a particular
identifiable event arrive at the same time as the visible light for that
event, even though the distance to the event is much less than the extinction
distance for x-rays. This gives strong evidence that the speed of light in a
vacuum is actually invariant and independent of the motion of the source.
|
|
|
|
With
the aid of modern spectroscopy we can now examine supernovae events in
detail, and it has been found that they exhibit several characteristic
emission lines, particularly the signature of atomic hydrogen at 6563
angstroms. Using this as a marker we can determine the Doppler shift of the
radiation, from which we can infer the speed of the source. The energy
emitted by a star going supernova is comparable to all the energy that it
emitted during millions or even billions of years of stable evolution. Three
main categories of supernovae have been identified, depending on the mass of
the original star and how much of its "nuclear fuel" remains. In
all cases the maximum luminosity occurs within just the first few days, and
drops by 2 or 3 magnitudes within a month, and by 5 or 6 magnitudes within a
year. Hence we can conclude that the light actually propagated through empty
space at a speed essentially independent of the speed of the sources.
|
|
|
|
Another
interesting observation involving the propagation of light was first proposed
in 1913 by De Sitter. He wondered whether, if we assume the speed of light in
a vacuum is always c with respect to the source, and if we assume a Galilean
spacetime, we would notice anything different in the appearances of things.
He considered the appearance of binary star systems, i.e., two stars that
orbit around each other. More than half of all the visible stars in the night
sky are actually binary stars, and the elements of their orbits may be
inferred from spectroscopic measurements of their radial speeds as seen from
the Earth. De Sitter's basic idea was that if two stars are orbiting each
other and we are observing them from the plane of their mutual orbit, the
stars will sometimes be moving toward the Earth rapidly, and sometimes away.
According to an emission theory this orbital component of velocity should be
added to or subtracted from the speed of light. As a result, over the
hundreds or thousands of years that it takes the light to reach the Earth,
the arrival times of the light from approaching and receding sources would be
very different.
|
|
|
|
Now,
before we go any further, we should point out a potential difficulty for this
kind of observation. The problem (again) is that the "vacuum" of
empty space is not really a perfect vacuum, but contains small and sparse
particles of dust and gas. Consequently it acts as a material and, as noted
above, light will reach it's steady-state velocity with respect to that
interstellar dust after having traveled beyond the extinction distance. Since
the extinction distance for visible light in interstellar space is quite
short, one could argue that the light will be moving at essentially c
relative to the interstellar gas for almost its entire travel time,
regardless of the original speed. For this reason, it's questionable whether
visual observations of celestial objects can provide good tests of emission
theory predictions. However, once again we can make use of the high-frequency
end of the spectrum to strengthen the tests. If we focus on light in the frequency
range of, say, x-rays and gamma rays, the extinction distance is much larger
than the distances to many binary star systems, so we can carry out De
Sitter's proposed observation (in principle) if we use x-rays, and this has
actually been done by Brecher in 1977.
|
|
|
|
With
the proviso that we will be focusing on light whose extinction distance is
much greater than the distance from the binary star system to Earth (making
the speed of the light simply c plus the speed of the star at the time of
emission), how should we expect a binary star system to appear? Let's
consider one of the stars in the binary system, and write its coordinates and
their derivatives as
|
|
|
|

|
|
|
|

|
|
|
|
where
D is the distance from the Earth to the center of the binary star system, R
is the radius of the star's orbit about the system's center, and ω is
the angular speed of the star. We also have the components of the emissive
light speed
|
|
|
|
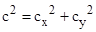
|
|
|
|
In
these terms we can write the components of the absolute speed of the light
emitted from the star at time t:
|
|
|
|

|
|
|
|
Now,
in order to reach the Earth at time T the light emitted at time t must travel
in the x direction from x(t) to 0 at a speed of 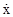 for a time Δt = T−t,
and similarly for the y direction. Hence we have for a time Δt = T−t,
and similarly for the y direction. Hence we have
|
|
|
|
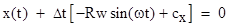
|
|
|
|
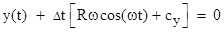
|
|
|
|
Substituting
for x, y, and the light speed derivatives 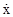 , , 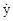 , we have , we have
|
|
|
|
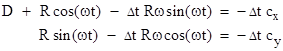
|
|
|
|
Squaring
both sides of both equations, and adding the resulting equations together,
gives
|
|
|
|
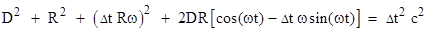
|
|
|
|
Re-arranging
terms gives the quadratic in Δt
|
|
|
|
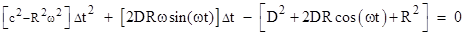
|
|
|
|
If
we define the normalized parameters
|
|
|
|
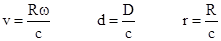
|
|
|
|
then
the quadratic in Δt becomes
|
|
|
|
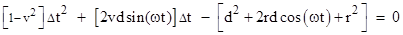
|
|
|
|
Solving
this quadratic for Δt = T−t
and then adding t to both sides gives the arrival time T on Earth as a
function of the emission time t on the star
|
|
|
|
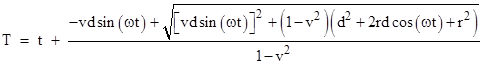
|
|
|
|
If
the star's speed v is much less than the speed of light, this can be
expressed very nearly as
|
|
|
|
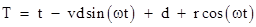
|
|
|
|
The
derivative of T with respect to t is
|
|
|
|
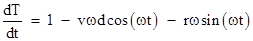
|
|
|
|
and
this takes it's minimum value when t = 0, where we have
|
|
|
|
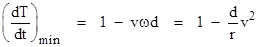
|
|
|
|
Consequently
we find the DeSitter effect, i.e., dT/dt goes negative if d > r/v2.
Now, we know from Kepler's third law (which also applies in relativistic
gravity with the appropriate choice of coordinates) that m = r3ω2
= rv2, so we can substitute m/r for v2 in our
inequality to give the condition d > r2/m. Thus if the distance
of the binary star system from Earth exceeds the square of the system's
orbital radius divided by the system's mass (in geometric units) we would
expect DeSitter's apparitions − assuming the speed of light is c ± v.
|
|
|
|
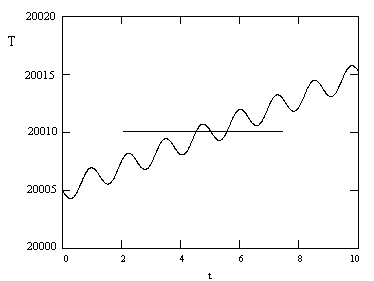
As
an example, for a binary star system a distance of d = 20000 light-years
away, with an orbital radius of r = 0.00001 light-years, and an orbital speed
of v = 0.00005, the arrival time of the light as a function of the emission
time is as shown below:
|
|
|
|
|
|
|
|
This
corresponds to a star system with only about 1/6 solar mass, and an orbital
radius of about 1.5 million kilometers. At any given reception time on Earth
we could (according to the emission theory) typically "see" at
least three separate emission events from the same star at different points
in its orbit. DeSitter tried to find evidence of this multiplicity of signals
in observations of many binary star systems, but none exhibited this effect.
He wrote
|
|
|
|
The observed
velocities of spectroscopic doubles are as a matter of fact satisfactorily
represented by a Keplerian motion. Moreover in many cases the orbit derived
from the radial velocities is confirmed by visual observations (as for δ
Equuli, ζ Herculis, etc.) or by eclipse observations (as in Algol
variables). We can thus not avoid the conclusion [that] the velocity of light
is independent of the motion of the source. Ritz’s theory would force us to
assume that the motion of the double stars is governed not by Newton’s law,
but by a much more complicated law, depending on the star’s distance from the
earth, which is evidently absurd.
|
|
|
|
Of
course, he was looking in the frequency range of visible light, which we've
noted is subject to extinction. However, in the x-ray range we can (in
principle) perform the same basic test, and yet we still find no traces of
multiple overlapping signals in binary stars, nor do we ever see the stellar
components going in "reverse time" as we would according to the
above profile. (Needless to say, for star systems at great distances it is
not possible to distinguish the changes in transverse positions but, as noted
above, by examining the Doppler shift of the radial components of their
motions we can infer the motions of the individual bodies.) Hence these
observations support the proposition that the speed of light in empty space
is essentially independent of the speed of the source.
|
|
|
|
In
comparison, if we take the relativistic approach with constant light speed c,
independent of the speed of the source, an analysis similar to the above
gives the approximate result
|
|
|
|
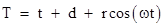
|
|
|
|
whose
derivative is
|
|
|
|
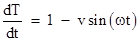
|
|
|
|
which
is always positive for any v less than 1. This means we can't possibly have
images arriving in reverse time, nor can we have any multiple appearances of
the components of the binary star system.
|
|
|
|
Regarding
this subject, Robert Shankland recalled Einstein telling him (in 1950) that
he had himself considered an emission theory of light, similar to Ritz's
theory, during the years before 1905, but he abandoned it because
|
|
|
|
he could think
of no form of differential equation which could have solutions representing
waves whose velocity depended on the motion of the source. In this case the
emission theory would lead to phase relations such that the propagated light
would be all badly "mixed up" and might even "back up on
itself". He asked me, "Do you understand that?" I said no, and
he carefully repeated it all. When he came to the "mixed up" part,
he waved his hands before his face and laughed, an open hearty laugh at the
idea!
|
|
|
|
Return to Table of Contents
|