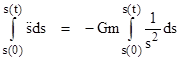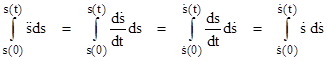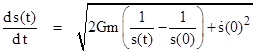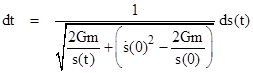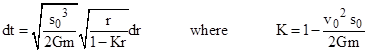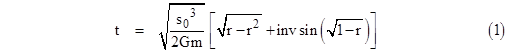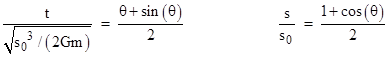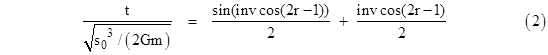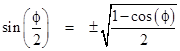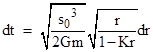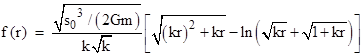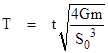4.3  Free-Fall Equations

When, therefore, I observe a stone initially at rest falling from an elevated position and continually acquiring new increments of speed, why should I not believe that such increases take place in a manner which is exceedingly simple and rather obvious to everybody?

                                                                                                  Galileo Galilei, 1638

As noted in the previous chapter, according to Newtonian physics the spatial separation between two particles of combined mass m in radial gravitational free-fall (i.e., with no angular momentum) satisfies the relation

where dots signify derivatives with respect to time. We will find in Section 6 that, according to general relativity, the radial position of a test particle as a function of the particle’s proper time in a spherically symmetrical gravitational field satisfies an equation of the same form, so it’s interesting from both a Newtonian and a relativistic standpoint to derive the explicit solution of this equation. Integrating both sides over ds from an arbitrary initial separation s(0) to the separation s(t) at some other time t gives

The left hand integral can be rewritten as

Therefore, the previous equation can easily be integrated to give

which shows that the quantity

is invariant for all t. Solving the equation for , we have

Rearranging this gives

To simplify the expressions, we put s₀ = s(0), v₀ =  and r = s(t)/s₀. In these terms, the preceding expression can be written

There are two cases to consider. If K is positive, then the trajectory is bounded, and there is some point on the trajectory (the apogee) at which v = 0. Choosing this point as our time origin t = 0, we have K=1, and the standard integral gives

This equation describes a (scaled) cycloidal relation between t and r, which can be expressed parametrically in terms of a fictitious angle θ as follows

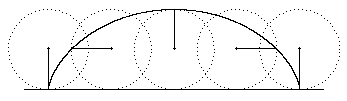
A cycloid is the curve traced by a point fixed on the perimeter of a wheel rolling along a flat surface, as illustrated in the figure below.

To verify that the two parametric equations are equivalent to (1), we can solve the second for θ and substitute into the first to give

Using the trigonometric identity  we see that the first term on the right side is

Also, letting ϕ = invcos(2r-1), we can use the trigonometric identity

to show that this angle is

so the second term on the right side of (2) is

which completes the demonstration that the cycloid relation given by (2) is equivalent to the free-fall relation (1).

The second case is when K is negative. For this case we can conveniently express the equations in terms of the positive parameter k = -K. The standard integral

tells us that, for any two points r₀ and r₁ on the trajectory, the time interval is related to the separations according to

where

Notice that if we define S₀ = s₀ / k and R = kr, then this becomes

Thus, if we define the normalized time parameter

then the normalized equation of motion is

This represents the shape of every non-rotating separation between two particles of combined mass m for which k is positive, which means that the absolute value of v₀ exceeds . These are the unbound radial orbits for which R goes to infinity, as opposed to the case when the absolute value of v₀ is less than this threshold, which gives bound radial orbits in the shape of a cycloid in accord with equation (1).

Return to Table of Contents