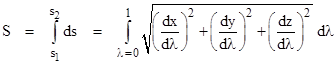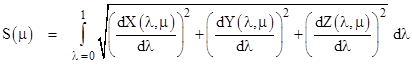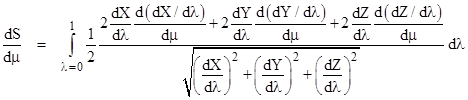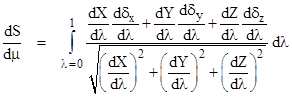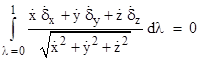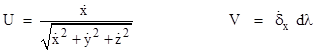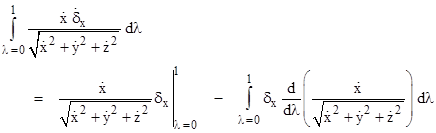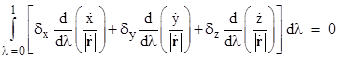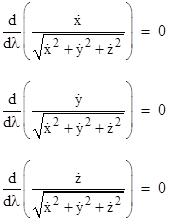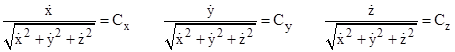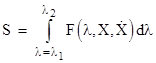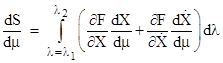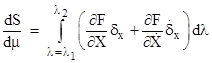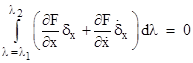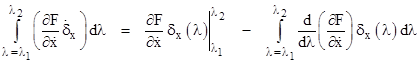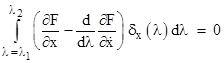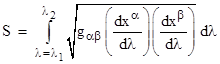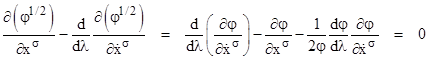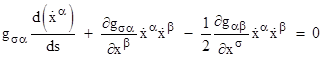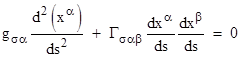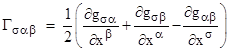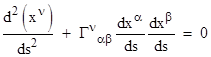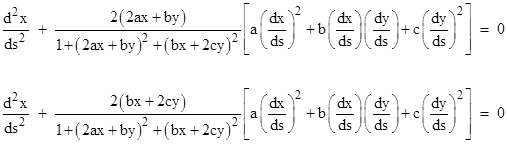Relatively Straight

There’s some end at last for the man who follows a path; mere rambling is interminable.

                                                                          Seneca, 60 AD

The principle of relativity, as expressed in Newton's first law of motion (and carried over essentially unchanged into Einstein's special theory of relativity) is based on the idea of uniform motion in a straight line. However, the terms "uniform motion" and "straight line" are not as easy to define as one might think. Historically, it was usually just assumed that such things exist, and that we know them when we see them. Admittedly there were attempts to describe these concepts, but mainly in somewhat vague and often circular ways. For example, Euclid tells us that "a line is breadthless length", and "a straight line is a line which lies evenly with the points on itself". The precise literal interpretation of these statements can be debated, but they seem to have been modeled on an earlier definition given by Plato, who said a straight line is "that of which the middle covers the ends". This in turn may have been based on Parmenides' saying that "straight is whatever has its middle directly between the ends".

Each of these definitions relies on some pre-existing idea of straightness to give meaning to such terms as "lying evenly" or "directly between", so they are immediately self-referential. Other early attempts to define straightness invoked visual alignment, on the presumption that light travels in a straight line. Of course, we could simply define straightness to be congruence with a path of light, but such an empirical definition would obviously preclude asking whether, in fact, light necessarily travels in straight lines as defined in some more abstract sense. Not surprisingly, thinkers like Plato and Euclid, who wished to keep geometry and mechanics strictly separate, preferred a purely abstract a priori definition of straightness, without appealing (explicitly) to any physical phenomena. Unfortunately, their attempts to provide a meaningful conceptual definition were not particularly successful.

Aristotle noted that among all possible lines connecting two given points, the straight line is the one with the shortest length, and Archimedes suggested that this property could be taken as the definition of a straight line. This at least has the merit of relating two potentially distinct concepts, straightness and length, and even gives us a way of quantifying which of two lines (i.e., curves) connecting two points is "straighter", simply by comparing their lengths, without explicitly invoking the straightness of anything else. Furthermore, this definition can be applied in a more general context, such as on the surface of the Earth, where the straightest (shortest) path between two points is an arc of a great circle, which is typically not congruent to a visual line of sight. We saw in Section 3.5 that Hero based his explanation of optical reflection on the hypothesis that light travels along the shortest possible path. This is a nice example of how an a priori conceptual definition of straightness led to a non-trivial physical theory about the behavior of light, which obviously would have been precluded if there had been no conception of straightness other than that it corresponds to the paths of light.

We've also seen how Fermat refined this principle of straightness to involve the variable of time, related to spatial distances by what he intuited was an invariant characteristic speed of light. Similarly the principle of least action, popularized by Maupertuis and Euler, represented the application of stationary paths in various phase spaces (i.e., the abstract space whose coordinates are the free variables describing the state of a system), but for actual geometrical space (and time) the old Euclidean concept of extrinsic straightness continued to predominate, both in mathematics and in physics. Even in the special theory of relativity Einstein relied on the intuitive Euclidean concept of straightness, although he was dissatisfied with this approach, and believed that the true principle of relativity should be based on the more profound Archimedian concept of straight lines as paths with extremal lengths. In a sense, this could be regarded as relativizing the concept of straightness, i.e., rather than seeking absolute extrinsic straightness, we focus instead on relative straightness of neighboring paths, and declare the extremum of the available paths to be "straight", or rather "as straight as possible".

In addition, Einstein was motivated by the classical idea of Copernicus that we should not regard our own particular frame of reference (or any other frame of reference) as special or preferred for the laws of physics. It ought to be possible to express the laws of physics in such a way that they apply to any system of coordinates, regardless of their state of motion. The special theory succeeds in this for all uniformly moving systems of coordinates (although with the epistemological shortcoming discussed in Section 4.7), but Einstein sought a more general theory of relativity encompassing coordinate systems in any state of motion and avoiding the circular definition of straightness.

We've noted that Archimedes suggested defining a straight line as the shortest path between two points, but how can we determine which of the infinitely many paths from any given point to another is the shortest? Let us imagine any arbitrary path through three-dimensional space from the point P₁ at (x₁,y₁,z₁) to the point P₂ at (x₂,y₂,z₂). We can completely describe this path by assigning a smooth monotonic parameter λ to the points of the path, such that λ=0 at P₁ and λ=1 at P₂, and then specifying the values of x(λ), y(λ), and z(λ) as functions of λ.  The total length S of the path can be found from the functions x(λ), y(λ), and z(λ) by integrating the differential distances all along the path as follows

Now suppose we let δ_x(λ), δ_y(λ), and δ_z(λ) denote three arbitrary functions of λ, representing some deviation from the nominal path, and consider the resulting "disturbed path" described by the functions

where μ is a parameter that we can vary to apply different fractions of the disturbance. For any fixed value of the parameter μ the distance along the path from P₁ to P₂ is given by

Our objective is to find functions x(λ), y(λ), z(λ) such that for any arbitrary disturbance vector δ, the value of S(μ) is minimized at μ = 0. Those functions will then describe the “straightest” path from P₁ to P₂.

To find the minimal value of S(μ) we differentiate with respect to μ. It's legitimate to perform this differentiation inside the integral, so (omitting the indications of functional dependencies) we can write

We can evaluate the derivatives with respect to λ based on the definitions of X,Y,Z as follows

Therefore, the derivatives of these with respect to μ are simply

Substituting these expressions into the previous equation gives

We want this quantity to equal zero when μ equals 0. In that case we have X=x, Y=y, and Z=z, so we make these substitutions and then require that the above integral vanish. Thus, letting dots denote differentiation with respect to λ, we have

Using "integration by parts" we can evaluate this integral, term by term. For example, considering just the x component in the numerator, we can use the "parts" variables

and then the usual formula for integration by parts gives

The first term on the right-hand side automatically vanishes, because by definition the disturbance components δ_x, δ_y, δ_z are all zero at the end-points of the path. Applying the same technique to the other components, we arrive at the following expression for the overall integral which we wish to set to zero

where

The coefficients of the three terms in the integrand are the disturbance functions δ_x, δ_y, δ_z, which are allowed to take on any arbitrary values in between λ = 0 and λ = 1. Regardless of the values of these three disturbance components, we require the integral to vanish. This is a very strong requirement, and can only be met by setting each of the three derivatives in parentheses to zero, i.e., it requires

This implies that the arguments of these three derivatives do not change as a function of the path parameter, so they have constant values all along the path. Thus we have

The numerators of these expressions can be regarded as the x, y, and z components, respectively, of the "rate" of motion (per λ) along the path, whereas the denominators represent the total magnitude of the motion. Thus, these conditions tell us that the components of motion along the path are in a constant ratio to each other, which means that the direction of motion is constant, i.e., a straight line. So, to reach from P₁ to P₂, the constants must be given by C_x = (x₂ – x₁)/D, C_y = (y₂ – y₁)/D, and C_z = (z₂ – z₁)/D, where D is the total distance given by D² = (x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)². Given an initial trajectory, the entire path is determined by the assumption that it proceeds from point to point always by the shortest possible route.

So far we have focused on finding the geodesic paths in ordinary Euclidean three-dimensional space, and found that they correspond to our usual notion of straight lines. However, in a space with a different metric, the shapes of geodesic paths can be more complicated. To determine the general equations for geodesic paths, let us first formalize the preceding "variational" technique. In general, suppose we wish to determine a function x(λ) from λ₁ to λ₂ such that the integral of some function F(λ,x,) along that path is stationary. (As before, dots signify derivatives with respect to λ.) We again define an arbitrary disturbance δ_x(x) and the disturbed function X(λ,μ) = x(λ) + μδ_x(λ), where μ is a parameter that determines how much of the disturbance is to be applied. We wish to make stationary the integral

This is done by differentiating S with respect to the parameter μ as follows

Substituting for dX/dμ and /dμ gives

We want to set this quantity to zero when μ = 0, which implies X = x, so we require

The integral of the second term in parentheses (integration by parts) is

The first term on the right-hand side is identically zero (since the disturbance is defined to be zero at the end points), so we can substitute the second term back into the preceding equation and factor out the disturbance δ_x(λ) to give

Again, since this equations must be satisfied for every possible (smooth) disturbance function δ_x(λ), it requires that the quantity in parentheses vanish identically, so we arrive at the Euler equation

which is the basis for solving a wide variety of problems in the calculus of variations.

The application of Euler's equation that most interests us is in finding the general equation of the straightest possible path in an arbitrary smooth manifold with a defined metric. In this case the function whose integral we wish to make stationary is the absolute spacetime interval, defined by the metric equation

where, as usual, summation is implied over repeated indices. Multiplying the right side by (dλ/dλ)² and taking the square root of both sides gives the differential "distance" ds along a path parameterized by λ. Integrating along the path from λ₁ and λ₂ gives the distance to be made stationary

For each individual coordinate x^σ this can be treated as a variational problem with the function

where again dots signify differentiation with respect to λ. (Incidentally, the metric need not be positive-definite, since we can always choose our sign convention so that the squared intervals in question are positive, provided we never integrate along a path for which the squared interval changes sign, which would represent changing from timelike to spacelike, or vice versa, in relativity.) Therefore, we can apply Euler's equation to immediately give the equations of geodesic paths on the surface with the specified metric

For n-dimensional space this represents n equations, one for each of the coordinates x¹, x², ..., xⁿ. Letting φ = (ds/dλ)² = F² =  this can be written as

To simplify these equations, let us put the parameter λ equal to the integrated path length s, so that we have φ = 1 and dφ/dλ = 0. The right-most term drops out, and we're left with

Notice that even though φ equals a constant 1 in these circumstances and the total derivative vanishes, the partial derivatives do not necessarily vanish. Indeed, if we substitute for  into this equation we get

Evaluating the derivative in the left-hand term and dividing through by 2, this gives

At this point it's conventional to make use of the identity

(where we have simply swapped the α and β indices) to represent the middle term of the preceding equation as half the sum of these two expressions. This enables us to write the geodesic equations in the form

where the symbol Γ_σαβ is defined as

These are called connection coefficients, also known as Christoffel symbols of the first kind. Finally, if we multiply through by the contravariant metric g^σν, we have

where

are known as Christoffel symbols of the second kind.

As an example, consider the simple two-dimensional surface h = ax² + bxy + cy² discussed in Section 5.3. Using the metric tensor, its inverse, and partial derivatives we can now directly compute the Christoffel symbols, from which we can give explicit parametric equations for the geodesic paths on our surface:

If we scale and rotate the coordinates so that the surface height has the form h = xy/R, the geodesic equations reduce to

These equations show that if either dx/ds or dy/ds equals zero, the second derivatives of x and y with respect to s must be zero, so lines of constant x and lines of constant y are geodesics (as expected, since these are straight lines in space). Given an initial trajectory that is not parallel to either the x or y axis the resulting geodesic path on this surface will be curved, and can be explicitly computed from the above formulas.

Return to Table of Contents