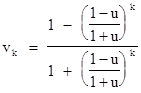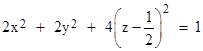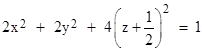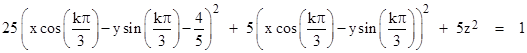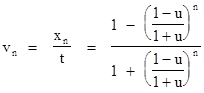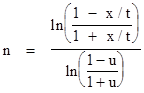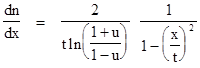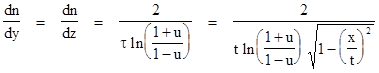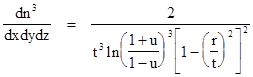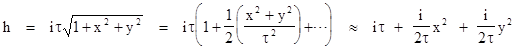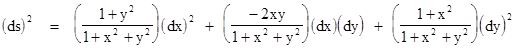7.5  Packing Universes In Spacetime

 

All experience is an arch wherethrough

Gleams that untraveled world whose margin fades

Forever and forever when I move.

                              Tennyson, 1842

 

One of the interesting aspects of the Minkowski metric is that every lightcone (in principle) contains infinitely many nearly-complete lightcones. Consider just a single spatial dimension in which an infinite number of point particles are moving away from each other with mutual velocities as shown below:

 

 

Each particle finds itself mid-way between its two nearest neighbors, which are receding at nearly the speed of light, so that each particle can be regarded as the origin of a nearly-complete lightcone. On the other hand, all of these particles emanate from a single point, and the entire infinite set of points (and nearly-complete lightcones) resides within the future lightcone of that single point.

 

More formally, a complete lightcone in a flat Lorentzian xt plane comprises the boundary of all points reachable from a given point P along world lines with speeds less than 1 relative to any and every inertial worldline through P. Also, relative to any specific inertial frame W we can define an "ε-complete lightcone" as the region reachable from P along world lines with speeds less than (1−ε) relative to W, for some arbitrarily small ε > 0. A complete lightcone contains infinitely many epsilon-complete lightcones, as illustrated above by the infinite linear sequence of particles in space, each receding with a speed of (1−ε) relative to its closest neighbors. Since we can never observe something infinitely red-shifted, it follows that our observable universe can fit inside an ε-complete lightcone just as well as in a truly complete lightcone. Thus a single lightcone in infinite flat Lorentzian spacetime encompasses infinitely many mutually exclusive ε-universes.

 

If we arbitrarily select one of the particles as the "rest" particle P0, and number the other particles sequentially, we can evaluate the velocities of the other particles with respect to the inertial coordinates of P0, whose velocity is v0 = 0. If each particle has a mutual velocity u relative to each of its nearest neighbors, then obviously P1 has a speed v1 = u. The speed of P2 is u relative to P1, and its speed relative to P0 is given by the relativistic speed composition formula v2 = (v1 + u)/(uv1 + 1). In general, the speed of Pk can be computed recursively based on the speed of Pk−1 using the formula

 

 

This is just a linear fractional function, so we can use the method described in Section 2.6 to derive the explicit formula

 

 

Similarly, in full 3+1 dimensional spacetime we can consider packing ε-complete lightspheres inside a complete lightsphere. A flash of light at point P in flat Lorentzian spacetime emanates outward in a spherical shell as viewed from any inertial worldline through P. We arbitrarily select one such worldline W0 as our frame of reference, and let the slices of simultaneity relative to this frame define a time parameter t. The points of the worldline W0 can be regarded as the stationary center of a 3D expanding sphere at each instant t. On any given time-slice t we can set up orthogonal space coordinates x,y,z relative to W0 and normalize the units so that the radius of the expanding lightsphere at time t equals 1. In these terms the boundary of the lightsphere is just the sphere

 

 

Now let W1 denote another inertial worldline through the point P with a velocity v = v1 relative to W0, and consider the region R1 surrounding W1 consisting of the points reachable from P with speeds not exceeding u = u1 relative to W1. The region R1 is spherical and centered on W1 relative to the frame of W1, but on any time-slice t (relative to W0) the region R1 has an ellipsoidal shape. If v is in the z direction then the cross-sectional boundary of R1 on the xy plane is given parametrically by

 

                          

 

as θ ranges from 0 to 2π. The entire boundary is just the surface of rotation of this ellipse about the z axis. If v1 has a magnitude of (1 − ε) for some arbitrarily small ε > 0, and if we set u1 = |v1|, then as ε goes to zero the boundary of the region R1 approaches the limiting ellipsoid

 

 

Similarly if W2 is an inertial worldline with speed |v2| = |v1| in the negative z direction relative to W0, then the boundary of the region R2 consisting of the points reachable from P with speeds not exceeding u2 = |v2| approaches the limiting ellipsoid    

 

 

The regions R1 and R2 are mutually exclusive, meeting only at the point of contact [0,0,0]. Each of these regions can be called an "ε-complete" lightsphere.

 

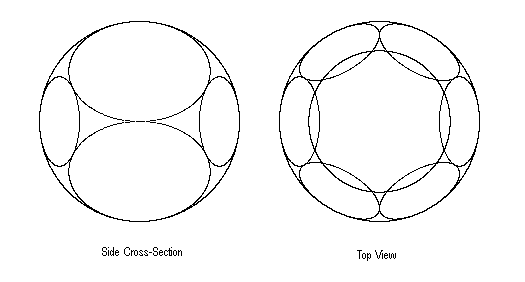
Interestingly, beginning with R1 and R2 we can construct a perfect tetrahedral packing of eight epsilon-complete lightspheres by placing six more spheres in a hexagonal ring about the z axis with centers in the xy plane, such that each sphere just touches R1 and R2 and its two adjacent neighbors in the ring. Each of these six spheres represents a region reachable from P with speeds less than u1 relative to one of six worldlines whose speeds are (1 − 4ε) relative to W0. The normalized boundaries of these six ellipsoids on a time-slice t are given by

 

 

for k = 0,1,..,5. In the limit as ε goes to zero the hexagonal cluster of ε-spheres touching any given ε-sphere becomes vanishingly small with respect to the given sphere's frame of reference, so we approach the condition that this hexagonal pattern tessellates the entire surface of each ε-sphere in a perfectly symmetrical tetrahedral packing of identical ε-complete lightspheres. A cross-sectional side-view and top-view of this configuration are shown below.

 

These considerations show that we can regard a single light cone as a cosmological model, taking advantage of the complete symmetry in Minkowski spacetime. Milne was the first to discuss this model in detail. He postulated a cloud of particles expanding in flat spacetime from a single event O, with a distribution of velocities such that the mutual velocities between neighboring particles was the same for every particle, just as in the one-dimensional case described at the beginning of this section. With respect to any particular system of inertial coordinates t,x,y,z whose origin is at the event O, the cloud of particles is spherically symmetrical with radially outward speed v = r/t. The density of the particles is also spherically symmetrical, but it is not isotropic. To determine the density with respect to the inertial coordinates t,x,y,z, we first consider the density in the radial direction at a point on the x axis at time t. If we let u denote the mutual speed between neighboring particles, then the speed vn of the nth particle away from the center is

 

 

where xn is the radial distance of the nth particle along the x axis. Solving for n gives

 

 

Differentiating with respect to x gives the density of particles in the x directions

 

 

This confirms that the one-dimensional density at the spatial origin drops in proportion to 1/t. Also, by symmetry, the densities in the transverse directions y and z at any point are given by this same expression as a function of the proper time τ  =  t at that point

 

 

This shows that the densities in the transverse directions are less than in the radial direction by a factor of . Neglecting the anisotropy, the number of particles in a volume element  dxdydz  at a radial distance r from the spatial origin at time t is proportional to

 

 

This distribution applies to every inertial system or coordinates with origin at O, so this cosmology looks the same, and is spherically symmetrical, with respect to the rest frame of each individual particle.

 

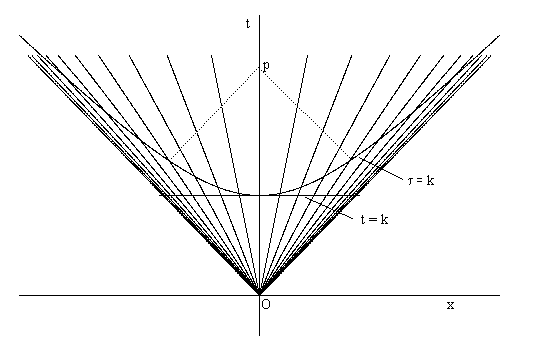
The above analysis was based on a foliation of spacetime into slices of constant-t for some particular system of inertial coordinates, but this is not the only possible foliation, nor even the most natural. From a cosmological standpoint we might adopt as our time coordinate at each point the proper time of uniform worldline extending from O to that point. This would give hyperboloid spacelike surfaces consisting of the locus of all the points with a fixed proper age from the origin event O. One of these spacelike slices is illustrated by the "τ = k" line in the figure below.

 

 

Rindler points out that if τ = k is the epoch at which the density of the expanding cloud drops low enough so that matter and thermal radiation decouple, we should expect at the present event "p" to be receiving an isotropic and highly red-shifted "background radiation" along the dotted lightlike line from that de-coupling surface as shown in the figure. As our present event p advances into the future we expect to see a progressively more red-shifted (i.e., lower temperature) background radiation. This simplistic model gives a surprisingly good representation of the 3°K microwave radiation that is actually observed.

 

It's also worth noting that if we adopt the hyperboloid foliation the universe of this expanding cloud is spatially infinite. We saw in Section 1.7 that the absolute radial distance along this surface from the spatial center to a point at r is

 

 

where r2 = x2 + y2 + z2 in terms of the inertial coordinates of the central spatial point. Furthermore, we can represent this hyperboloid spatial surface as existing over the flat Euclidean xy plane with the elevation . By making the elevation imaginary, we capture the indefinite character of the surface. In the limit near the origin we can expand h to give

 

 

So, according to the terminology of Section 5.3, we have a surface tangent to the xy plane at the origin with elevation given by  h = ax2 + bxy + cy2  where  a = c = i/2τ  and b = 0. Consequently the Gaussian curvature of this spatial surface is K = 4ac − b2 = -1/τ2. By symmetry the same analysis is applicable at every point on the surface, so this surface has constant negative curvature. This applies to any two-dimensional spatial tangent plane in the three-dimensional space at each point for constant τ.

 

We can also evaluate the metric on this two-dimensional spacelike slice, by writing the total differential of h

 

 

Squaring this and adding the result to (dx)2 + (dy)2 gives the line element for this surface in terms of the tangent xy plane coordinates projected onto the surface

 

 

Return to Table of Contents