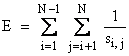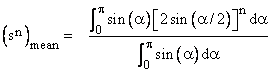|
Min-Energy Configurations of Electrons On A Sphere |
|
|
|
The determination of the stable equilibrium configurations of N particles confined to the surface of a sphere and repelling each other by a specified force law (such as an inverse square force) is known as Thomson’s Problem, named after J. J. Thomson, who studied such configurations in relation to his “plum pudding” model of the atom. The model turned out not to be viable, but the problem of determining equilibrium configurations has continued to be studied, and has been found relevant to a variety of physical phenomena, as well as being of purely mathematical interest. |
|
|
|
The vertices of the five Platonic solids give the only perfectly symmetrical distributions of points on the surface of a sphere. Therefore, if N positively charged particles are constrained to the surface of a sphere, and N is not equal to the number of vertices of a Platonic solid, then the particles must have an equilibrium configuration that is not perfectly symmetrical. It turns out that, even if N is a “Platonic number”, the equilibrium configuration is not necessarily the corresponding Platonic solid. In this note we describe the equilibrium configurations for values of N up to 32. |
|
|
|
The sphere is normalized to a radius of 1, and the force law between particles is assumed to be of the inverse-square type, so the equilibrium configuration of N particles is the set of N(N-1)/2 separations si,j such that |
|
|
|
|
|
|
|
is a minimum. The equilibrium configurations for the first several N are described below. |
|
|
|
N = 0: This leaves the sphere empty. |
|
|
|
N = 1: The case of a single particle. |
|
|
|
N = 2: Two particles go to opposite points on the sphere, and the line between them is a diameter of the sphere, having length 2. Thus, E = 0.5. |
|
|
|
N = 3: Three particles produce an equilateral
triangle on a great circle of the sphere. The three separations between
particles are each of length |
|
|
|
N = 4: Four points arrange themselves at the
vertices of a tetrahedron. The six separations between particles are each of
length |
|
|
|
N = 5: Five points give a north/south pole and an equilateral
triangle at the equator. Of the ten separations, one is of length 2, six are
of length |
|
|
|
N = 6: Six particles arrange themselves as the
vertices of an octahedron. Of the 15 separations between particles, three
are mutually perpendicular diameters of length 2, and the remaining twelve
are of length |
|
|
|
N = 7: Seven points give north/south poles and an
equilateral pentagon at the equator. Of the 21 separations between
particles, one is a diameter of length 2, ten are of length |
|
|
|
|
|
|
|
This gives |
|
|
|
|
|
N = 8: Eight particles arrange themselves into two squares on parallel planes, with the squares rotated by 45 degrees relative to each other. The 28 separations between particles come in the following four lengths: |
|
|
|
a = 1.2876935 b = 1.8968930 c = 1.6563945 d = 1.1712477 |
|
|
|
We observe that c = d |
|
in a stable equilibrium configuration. In other words, perfect symmetry does not imply stable equilibrium. |
|
|
|
N = 9: Nine points on the surface of a sphere will configure themselves as three equilateral triangles on parallel planes. One triangle is at the equator of the sphere, while the other two are located at latitudes above and below, and oriented at 60 degrees relative to the equator triangle. Looking down from above the north pole, the three triangles would appear as shown below: |
|
|
|
|
|
|
|
The separations between points have 6 distinct magnitudes, as summarized below. |
|
|
|
1.8496207 (1,6) (7,6) (2,4) (8,4) (3,5) (9,5) |
|
1.1355402 (1,4) (1,5) (7,4) (7,5) (3,4) (3,6) |
|
(9,4) (9,6) (2,5) (2,6) (8,5) (8,6) |
|
1.8695243 (1,8) (1,9) (2,7) (2,9) (3,7) (3,8) |
|
1.4072969 (1,7) (2,8) (3,9) |
|
1.2307059 (1,2) (1,3) (2,3) (7,8) (7,9) (8,9) |
|
1.7320509 (4,5) (4,6) (5,6) [distance = square root of 3] |
|
|
|
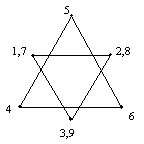
N = 10: Ten points on the surface of a sphere will arrange themselves with one north-south polar axis and two squares at equal and opposite latitudes, oriented at 45 degrees relative to each other. When viewed from above the north pole the points would appear as shown below. |
|
|
|
|
|
|
|
The separations come in 7 distinct lengths, summarized as follows: |
|
|
|
1.8758698 (1,6) (1,7) (1,8) (1,9) (10,2) (10,3) (10,4) (10,5) |
|
1.0745353 (1,2) (1,3) (1,4) (1,5) (10,6) (10,7) (10,8) (10,9) |
|
1.8125511 (3,5) (2,4) (6,8) (7,9) |
|
1.2816593 (2,3) (3,4) (4,5) (5,2) (6,7) (7,8) (8,9) (9,6) |
|
1.0935212 (2,7) (7,3) (3,8) (8,4) (4,9) (9,5) (5,6) (6,2) |
|
1.6868248 (2,8) (2,9) (3,6) (3,9) (4,6) (4,7) (5,7) (5,8) |
|
2.0000000 (1,10) |
|
|
|
|
|
|
|
|
|
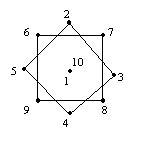
N=11: The equilibrium configuration of 11 charged particles on the surface of a sphere has one particle at the north pole (level 0). At a depth of 0.484692 (level 1) down from the north pole are two particles on opposite sides. Then at a depth of 0.6714 (level 2) are four particles in an oblong rectangle oriented at right angles to the previous two particles. The dimensions of this rectangle are 0.9778448 by 1.7118527, and it has diagonals of 1.9714513. Next, at a depth of 1.552681 (level 3) below the pole, are two particles on opposite longitudes, oriented parallel to the first two points below the pole. Interestingly, these two points are very nearly whole diameters away from the two particles on level 1. They are each 1.9995113 away from the opposite particle on the other level. At the lowest level, 1.805954 (level 4) below the pole, are two particles on opposite longitudes, oriented at right angles to the previous two. The arrangement of particles on each level is illustrated below: |
|
|
|
|
|
|
|
This configuration has separations of 20 distinct magnitudes, as summarized below. |
|
|
|
separation number example separation number example |
|
---------- ------ ------- ---------- ------ ------- |
|
1.6323310 4 (1,2) 0.9940217 4 (1,3) |
|
1.2896824 4 (1,4) 1.8123901 4 (1,5) |
|
1.7118527 2 (1,6) 0.9778448 2 (1,7) |
|
1.1709697 4 (1,8) 1.1216075 4 (1,9) |
|
1.9714513 2 (1,10) 1.7323473 4 (1,11) |
|
1.7140111 1 (2,3) 0.9845739 2 (2,4) |
|
1.6824472 4 (2,5) 1.9995113 2 (2,8) |
|
1.0682496 2 (2,11) 1.9005025 2 (4,5) |
|
1.7622040 2 (4,8) 1.0531511 4 (5,11) |
|
1.1839539 1 (5,9) 1.6667852 1 (8,11) |
|
|
|
N=12: The equilibrium configuration of 12 charged particles on the surface of a sphere is as the vertices of an icosahedron, one of the five Platonic solids. The 66 separations come in 3 distinct sizes, as summarized below: |
|
|
|
separation number |
|
---------- ------ |
|
1.0514622 30 |
|
1.7013016 30 |
|
2.0000000 6 |
|
|
|
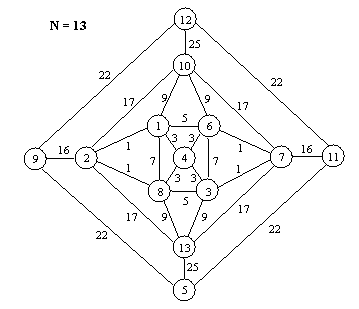
N=13: The stable equilibrium configuration of 13 particles involves 28 distinct distances, summarized in the tables presented at the end of this note. We also give an array identifying which of the 28 distances applies to each pair of particles. Symmetries of the configuration correspond to permutations of the particles that leave this array of pairwise distances unchanged. The configuration of 13 particles has no polar axis of two diametrically opposite particles, but it does have an axis of symmetry. The diagram below shows, schematically, how the particles are arranged, with the arbitrary identifying numbers taken from the summary table. The particles 9,2,4,7,11 all lie in a single central plane, as do the particles 12,10,4,13,5, and the configuration is symmetrical under reflection about either of these planes. The configuration is also symmetrical under rotation through p about the axis of particle 4. These two reflections and one rotation (along with the identity), are the only complete symmetries of this configuration. |
|
|
|
|
|
|
|
We note that the “squares” 2,10,7,13 and 9,12,11,5 are not actually plane squares, but are “folded” along their diagonals. |
|
|
|
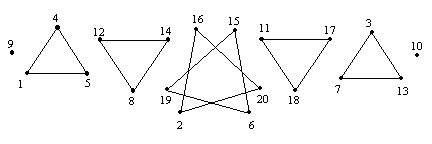
N=16: This is the first occurrence of more than 1 distinct local equilibrium configuration. The two configurations have energies |
|
|
|
C16.1: 92.91165530254497 |
|
C16.2: 92.92035396234466 |
|
|
|
These two configurations are shown in the figure below. |
|
|
|
|
|
|
|
Notice that C16.2 has two opposing "square faces", whereas C16.1 has only triangular faces. |
|
|
|
N = 19: The minimum-energy configuration of 19 charged particles on a sphere has a north pole, but no south pole. The remaining particles are on six lower planes. Immediately below the north pole is a rectangle, then a dipole at 90 degrees, then another rectangle (aligned with the dipole), then another dipole (aligned with the first rectangle’s major axis), then another rectangle (aligned with the first), then a dipole aligned with the first rectangle, and finally another dipole aligned with the second rectangle. The arrangements of particles on these seven levels are shown schematically in the diagram below, with particle designation numbers from the tables at the end of this note. |
|
|
|
|
|
|
|
From this schematic it is clear that the configuration has three symmetries, namely, a rotation through 180 degrees about the axis of particle 9, and two reflections (horizontal and vertical. |
|
|
|
N=20: The equilibrium configuration of 20 charged particles on the surface of a sphere has a north and south pole. Below the north pole is an equilateral triangle of three particles. On the next lower level is another equilateral triangle of three particles, rotated by 60 degrees. On the next lower level, the equator, there are six particles, arranged in two equilateral triangles. These triangles are skewed, but not by 60 degrees. Then there are two more levels of equilateral triangles, and then the south pole. The configuration at each level is illustrated below. |
|
|
|
|
|
|
|
The separations have 26 distinct magnitudes, as summarized below: |
|
|
|
separation number example separation number example |
|
---------- ------ ------- ---------- ------ -------- |
|
0.8331592 12 (1,2) 0.7894919 12 (2,8) |
|
1.8657231 6 (1,3) 1.4142136 12 (2,9) |
|
1.2478910 6 (1,4) 1.3615374 12 (2,11) |
|
1.4578665 12 (1,6) 1.8769439 12 (2,14) |
|
1.3869718 3 (1,7) 1.9924151 3 (2,15) |
|
0.8016163 12 (1,8) 1.7320508 6 (2,16) |
|
0.7829612 6 (1,9) 0.8455036 3 (2,19) |
|
1.8403727 6 (1,10) 0.9568466 6 (8,9) |
|
1.4651562 12 (1,11) 1.7562587 6 (8,10) |
|
1.5680184 6 (1,14) 1.8149394 6 (8,11) |
|
1.7833875 12 (1,15) 1.4553299 6 (8,12) |
|
1.9906722 6 (1,17) 1.0844446 3 (8,18) |
|
1.1469114 3 (2,6) 2.0000000 1 (9,10) |
|
|
|
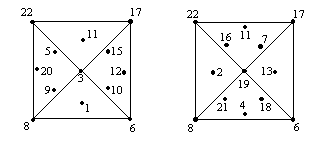
N = 22: The stable equilibrium configuration of twenty-two particles on the surface of a sphere is with 6 of the points arranged as the vertices of an octahedron. Then, in the northern hemisphere, two opposing faces have a particle located at the center of the triangular face. Similarly in the southern hemisphere, the two orthogonal opposing faces have a central particle. Then from each of these four face-centered particles you can imagine proceeding in three directions straight toward the edge of the respective triangle, and then a little beyond, where another particle is located. Thus, for each of the face-centered particles there are three other particles, giving 4 + (3)(4) + 6 = 22 total. |
|
|
|
In the drawing below, the six particles 22, 17, 6, 8, 3, and 19 are configured as the vertices of an octahedron. The four face-centered particles are 11, 1, 2, and 13. |
|
|
|
|
|
top view of upper top view of lower |
|
hemisphere hemisphere |
|
|
|
The 231 separations between particles come in 17 distinct lengths, summarized as follows: |
|
|
|
separation number example |
|
--------- ------- ------- |
|
1.6329932 6 (1,2) |
|
0.9194017 12 (1,3) |
|
0.7379041 12 (1,4) |
|
1.3559300 24 (1,5) |
|
1.9438121 12 (1,7) |
|
1.7761477 12 (1,17) |
|
1.5098498 12 (3,4) |
|
0.7743894 24 (3,5) |
|
1.4142136 12 (3,6) |
|
1.8439959 24 (3,7) |
|
1.3116225 12 (3,12) |
|
2.0000000 3 (3,19) |
|
1.7263978 24 (4,5) |
|
1.1879164 12 (4,9) |
|
1.9803530 6 (4,11) |
|
1.4279710 12 (4,12) |
|
0.7924366 12 (4,18) |
|
|
|
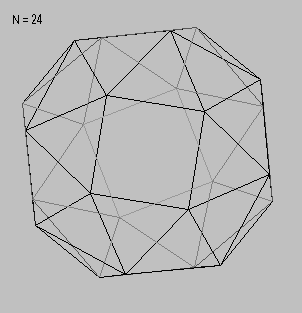
N=24: The convex solid formed by these vertices has several interesting symmetry properties. It has 6 square faces and 32 triangular faces, and a total of 60 edges. Here is one specific side view, aligned so that four of the square faces are seen as edges of the outer perimeter of the outline: |
|
|
|
|
|
|
|
|
|
N = 25: The stable equilibrium configurations of 21 particles involves 160 distinct pair-wise distances, as summarized in the tables at the end of this note. Most of the distances appear exactly twice, but 20 of them appear only once. These 20 distances split naturally into two sets of 10, one of which is the ten pairwise separations between the particles denoted by 6, 13, 16, 18, 20 in the summary tables for this configuration. If two particles are separated by a unique distance, the only possible alterations of those points in a symmetry transformation is to transpose them. If a particle is the terminus for more than one unique distance, it follows that it must remain fixed in any symmetry transformation. Furthermore, if there is such a transformation, it can only be a reflection about the plane containing those particles, which must therefore be a central plane (i.e., a plane passing through the origin). So it is in this case, as we find that the five particles 6,13,16,18,20 all lie on a single central plane. The other 10 unique distances involve just two particles each, namely, the pairs (1,9), (2,23), (3,8), (4,24), (5,11), (7,17), (10,22), (12,14), (15,21), and (19,25). These pairs of particles are symmetrical on either side of the central plane just mentioned, and accordingly we find that the only set of transpositions the leave the distance array unchanged is if all the transpositions are applied. Hence this is the only complete symmetry. |
|
|
|
N = 26: The unique minimum-energy configuration for 26 particles involves 168 distinct distances, of which 13 occur only once, 154 occur twice, and 1 occurs four times. Each of the 26 particles is a terminus of exactly one of the 13 singly-occurring distances. The pairings are indicated in parentheses next to the respective distances below: |
|
|
|
7 1.240911952398 ( 1, 8) |
|
32 1.695792857314 ( 2,10) |
|
59 1.945346859230 ( 3,16) |
|
84 1.678309456034 ( 4,22) |
|
91 0.715858022112 ( 5, 9) |
|
116 1.990984069713 ( 6,21) |
|
130 0.860576536055 ( 7,24) |
|
133 1.955722956319 (11,12) |
|
151 1.130614843242 (13,25) |
|
159 1.647267885398 (14,26) |
|
163 1.960650233462 (15,20) |
|
165 1.779648256635 (17,18) |
|
168 1.901864948467 (19,23) |
|
|
|
The only permutations of the particles leaving the distance array unchanged must consist of some subset of these transpositions, and it can be shown that the only symmetrical permutation (other than the identity) is the union of all these transpositions. This represents a rotation through 180 degrees. The unique distance occurring times, and the pairs of particles separated by this distance, are listed below. |
|
|
|
97 1.686814675682 (9,18) (5,17) (6,25) (13,21) |
|
|
|
Summary |
|
The following is a top-level summary of the stable equilibrium configurations of N particles for N = 0 to 32, followed by tables giving detailed specifications for each of these configurations. |
|
|
|
SUMMARY OF N-PARTICLE CONFIGURATIONS |
|
|
|
N seps dist poles description |
|
-- --- --- ---- ------------------------------------------- |
|
0 0 0 0 |
|
1 0 0 0 North pole. |
|
2 1 1 1 North and south poles. |
|
3 3 1 0 Triangle at equator. |
|
4 6 1 0 Tetrahedron. |
|
5 10 3 1 North and south pole with triangle at equator. |
|
6 15 2 3 Octahedron. |
|
7 21 4 1 North and south poles with pentagon at equator. |
|
8 28 4 0 Twisted cube; opposite squares at 45 degrees. |
|
9 36 6 0 Three parallel triangles, one at equator, at 60 deg. |
|
10 45 7 1 North and south pole with two skewed squares. |
|
11 55 20 0 Pole, line, rectangle, line, line. |
|
12 66 3 6 Icosahedron. |
|
13 78 28 0 Two reflection and one rotation symmetry. |
|
14 91 9 1 |
|
15 105 21 0 |
|
16 120 12,13 0 Two distinct configs; contains N=4 as subset. |
|
17 136 14 1 Contains N=7 as a subset. |
|
18 153 18 1 |
|
19 171 52 0 Pole, rec, line, rec, line, line, rec. |
|
20 190 26 1 Pole, tri, tria, double tri, tri, tri, pole. |
|
21 210 69 |
|
22 231 17 3 Contains N=6 (octahedron) as a subset. |
|
23 253 48 1 North and south pole, with 7 parallel triangles, one |
|
at equator and 3 on either side. Contains N=5 as a |
|
subset. |
|
24 276 16 0 Symmetries of snub cube. |
|
25 300 160 0 Five particles on central plane, ten on either side, |
|
symmetrical under reflection about the plane. |
|
26 325 168 0 A single rotation symmetry. |
|
27 351 30 |
|
28 378 35 |
|
29 406 75 |
|
30 435 118 |
|
31 465 93 |
|
32 496 11,43 |
|
|
|
Following are links to summaries and images of the minimal-energy configurations of N particles for N up to 32: |
|
|
|
|
|
Of all these solutions, the most appealing in some ways is the case N = 4! = 24, which is a polyhedron whose surface includes 24/4 perfect squares, 24/3 perfect triangles, 24/2 "bi-gons", and 24/1 “mono-gons” (i.e., individual points), arranged so that each vertex is identical. In addition, the vertices have a "handedness", so there are really two distinct versions of this solid. If your browser supports Javascript you can see a rotating image of this solid here. The solid formed by these vertices is very similar to the Archimedean solid called a “snub cube”, and it has the same symmetry group (O, in the Schoenflies notation), but it isn’t actually a snub cube, because it has edges of three different lengths. |
|
|
|
It appears from these results that the average energy per bond converges on unity as N increases. (For N = 4 the average energy per bond is 1.63, and by N = 32 this has dropped to 1.20.) This is consistent with the mean inverse distance between points on a unit sphere. To see this, we need only determine the mean distance of the points of a sphere from any given point on the sphere. Note that the distance s between two points separated by a central angle a is s = 2sin(a/2). All the points separated from a given point by this angle describe a circle of radius sin(a), so this is the “weight factor” for this distance. Hence the mean value of sn for any exponent n (for which the mean exists) is given by |
|
|
|
|
|
|
|
Evaluating the integrals leads to the closed-form solution |
|
|
|
|
|
|
|
Setting n = -1 gives the mean reciprocal distance as 1. The integral converges for any n greater than -2. Coincidentally, this is the reciprocal of the probability of n+2 randomly selected points on a circle all falling within the same half-circle (as discussed in another note). |
|
|
|
Stable equilibrium configurations of N particles have lately been determined for very large values of N. As noted above, the number of local minima (of energy) increases for large N, so people often focus on just the unique global minimum configuration. The first such configuration with no symmetry is N = 61, followed by 140, 149, 176, 179, 183, and so on. As N increases, the fraction of cases with no symmetry also increases. |
|
|
|
The energy differences between neighboring configurations become so slight for large values of N that the precise minima hardly seem very distinct. It would be of more interest to consider the dynamical flows, with kinetic energy conserved. In particular, it would be interesting to know if there are initial conditions that lead to stable periodic flow patterns, or if all orbits highly chaotic. |
|
|