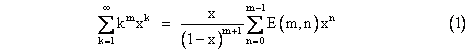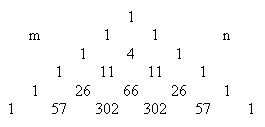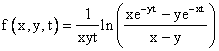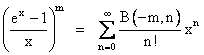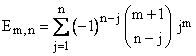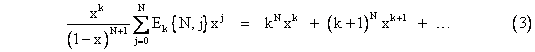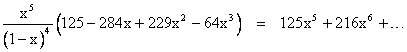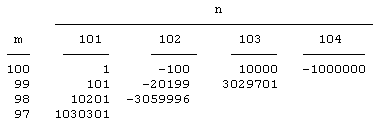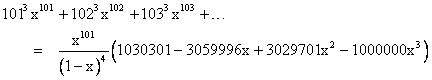Eulerian Numbers

Beginning with the geometric series

which converges for all |x| < 1, we can repeatedly differentiate and multiply by x to give the sequence of identities

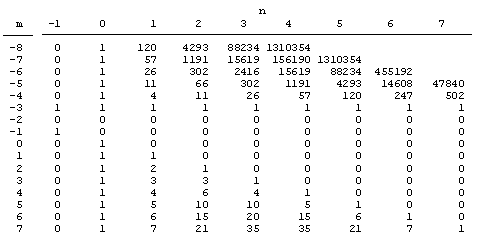
and so on. The coefficients of the numerator polynomials on the right side are as shown below.

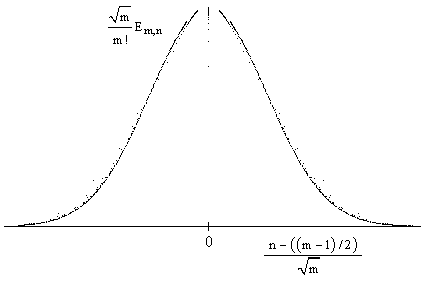
The sum of the mth row equals the factorial of m. Also, the mth row interpreted as a histogram approaches a normal distribution (just as do the binomial coefficients). The figure below shows a plot of the Eulerian numbers for m = 1 to 85, re-scaled as indicated.

Letting E(m,n) denote the value from the mth row and nth column, we have the general identity

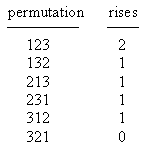
Not surprisingly, the Eulerian numbers have many combinatorial applications. The most famous is the fact that the nth number in the mth row represents the number of permutations of m objects that have exactly n "rises". For example, the six possible permutations of three objects, along with the number of "rises" (i.e., the number of times it goes from a lower to a higher number, reading left to right) are shown below

Thus the numbers of permutations having exactly 0, 1, and 2 rises are 1, 4, and 1 respectively, and these numbers comprise the 3rd row of Eulerian numbers.

If we arrange the Eulerian Numbers with symmetrical indices as shown below

then they can be generated by the well-known recurrence

In addition, they have the interesting generating function

The coefficient of  x^m-1 y^n-1 (-t)^m+n-1 / (m+n)!  is the Eulerian number E[m,n]. Thus we have

I found this by a very indirect approach. Is there a simple procedure for deducing the generating function - if one exists - for a given array of numbers?

There's also a nice relation between Eulerian numbers and the generalized Bernoulli numbers. Let W(m,n) be a weighted average of the nth powers of the first m natural numbers, using the Eulerians as the weights. For example

For m>n it turns out that W(m,n) equals B(-m,n), the generalized Bernoulli number, which can be defined as the coefficients in the expansion

Beginning at the "diagonal" where m=n, the values of W and B begin to differ, although they differ only half the time on the diagonal. Specifically, the differences B(-m,m) - W(m,m) for m = 0,1,2,3... along the diagonal are

which of course are just the ordinary Bernoulli numbers.

The Eulerian numbers can also be used to give a closed-form expression for the sums of powers (and sums of sums of powers, etc.) of the first n positive integers, as discussed in the note on Sums and Differences of Discrete Functions. In that note we derive the closed form expression for the Eulerian numbers

There is also an interesting relation between the Eulerian Numbers and the binomial coefficients. The most obvious recurrence relation satisfied by the binomial coefficients is

but they also satisfy the recurrence

Interestingly, this formula also generates the Eulerian numbers, so both sets of numbers can be regarded as simply different regions of a single array. Here's a brief table of the combined binomial and Eulerian numbers.

On the other hand, it is sometimes convenient to write the array of Eulerian numbers in "rectangular form" as follows:

With these indicies the Eulerians satisfy the recurrence relation

The fact that I've negated the "m" index may seem strange, but it leads to a natural generalization. Suppose that instead of dealing with infinite series, we want an expression for the finite sum

Obviously if N = 0 this sum is given by the simple Euclidean expression

but what about higher values of N? Clearly if we had an expression for the infinite sum

we could subtract it from our original infinite sum (1) to give the desired finite sum. So, our objective is to find a closed form expression for (2). Notice that if we multiply the basic geometric series by x^k, we can proceed as before, alternately differentiating and multiplying x to give

where the coefficients E_k{N,j} are taken from an array of number somewhat similar to the Eulerian numbers. Of course, if k = 0 these coefficients are the Eulerian numbers. For other values of k we can generate the coefficients E_k{m,n} (using "rectangular indicies") with the same recurrence as for the standard Eulerians, except that we "slide the indicies around the corner". This is best illustrated with an example. For the case k = 5 we are seeking a closed-form expression for the infinite sum

This is given by (3) with the values of E_k{N,j} taken from the following table for E₅{m,n} (and appropriately converting their indicies from the rectangular to the triangular array format):

So, with k = 5 and N = 3, equation (3) gives the identity

Subtracting this from (1) with N=3 gives, as expected

For a less trivial example, suppose we want an abbreviated expression for the finite sum

The procedure is just the same, except that we have k = 101 instead of k = 3, so we need to slide the indicies further around the corner. In other words, the coefficient array with k = 101 is

By the way, a convenient check on the accuracy of these coefficients is to notice that, just as in the case of the basic Eulerian numbers, the sum of the jth diagonal is j!. This table gives us the closed-form expression for the infinite sum

so again we can subtract this from the simple closed-form expression for the infinite sum given by (1) with N=3 to represent the polynomial f(x) of degree 100.

Incidentally, the process of differentiating and multiplying by x can be reversed to give expressions for infinite sums whose coefficients are the inverses of powers of integers. To reverse the process we integrate both sides of the basic geometric series, which gives the well-known expansion for the natural log

Diving by x and integrating then gives the relation

This is the same formula that appears in the note Average of s(n)/n describing the relation between the sum-of-divisor function and the sum of the inverse squares.

Return to MathPages Main Menu