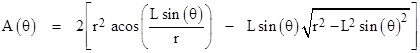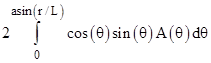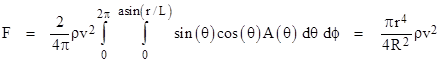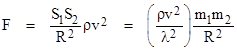Historical Assessments of the Fatio-Lesage Theory

It’s an interesting historical fact that the attitudes of scientists toward the Fatio-Lesage “explanation” of  gravity have varied widely, not just from one scientist to another, but for individual scientists at different moments. This is exemplified by Newton’s ambivalence. On one hand, he told Fatio that if gravity had a mechanical cause, then the mechanism must be the one Fatio had described. On the other hand, Newton usually inclined toward the view that gravity does not have a mechanical (material) cause. It’s true that he explicitly denied (in a famous letter to Bentley) the intelligibility of bare action at a distance, but he just as explicitly rejected (in a letter to Leibniz) the notion that space is filled with some material substance (a la Descartes) that communicates the force of gravity. His alternative was to say that gravity is caused by the will and spirit of God, not by any material cause. Of course, he gave consideration to various possible material mechanisms, and even included some Queries in the latter editions of Opticks, speculating on the possibility of an ether that is least dense near matter, and whose density increases the further we recede from matter. This could be interpreted as a somewhat obscure reference to Fatio’s theory, since the flux of gravific corpuscles is reduced in the vicinity of matter, due to the shadowing effect. And yet David Gregory reported that, behind Fatio’s back, Newton laughed at his method of explaining gravity, and Newton scrupulously avoided mentioning any such explanations in his cherished Principia – aside from making it clear that his conception of gravity did not assume any particular mechanism, nor even whether gravity was due to an inherent pull between matter or was caused by some kind of impulsion. Indeed Fatio was unhappy that Newton never publicly acknowledged, let alone endorsed, his theory. He wrote to Conduitt in 1730

I have often wondered how the second and third Edition of Sir Isaac Newton’s Principles do touch so lightly upon this matter. For if there be a mechanical cause of gravity – as it is most probable – there is also a demonstration that there can be no cause of it than that which I give, and Dr. I. knew it very well.

Apparently Fatio didn’t appreciate how anathema his “explanation of gravity” was to Newton’s fundamental doctrine, which was to eschew occult (i.e., hidden) causes for manifest phenomena. Even setting outside the outlandishness of the explanation, Newton was never able to extract from Fatio’s idea any testable consequence that could support it, so the idea remained an occult mechanism which, according to Newton, is not the proper purview of science.

Subsequent scientists have had similarly ambivalent reactions to the theory of Fatio and Lesage. For example, Euler originally expressed interest in Le Sage’s theory, stating (in the same conditional manner employed by Newton) that if gravity is due solely to impulse forces, then something like Lesage’s theory must be true. However, Euler ultimately rejected Lesage’s theory, and when Lesage persisted in trying to persuade him, Euler finally replied

So you must excuse me Sir, if I have a great repugnance for your corpuscles ultramundane, and I shall always prefer to confess my ignorance of the cause of gravity than to have recourse to such strange hypotheses.

This striking ambivalence regarding the Fatio-Lesage theory has many other examples. Herschel spoke for many scientists when he said it was “too grotesque to need serious consideration”, whereas Thomson and Tait gave it serious consideration, the latter even asserting that it was “the only plausible answer which has yet been propounded”. Darwin too gave the idea “serious consideration”, but he also said “no man of science is disposed to accept it as affording the true road”.

Several of the founders of modern kinetic theory, including both John Herapath in 1820 and John James Waterston in 1845, began their investigations by trying to devise mechanical explanations of gravity. Herapath seems to have been influenced explicitly by Lesage’s writings, whereas Waterston was apparently one of the many independent discoverers of the concept. However, it must also be said that, as the principles of kinetic theory emerged, the plausibility of a Lesagean explanation of gravity was diminished rather than increased. Subsequently, Thomson and Tait (who dubbed themselves T and T’) were intrigued by the Fatio/Lesage concept, although Thomson pointed out that the theory was untenable if the ultra-mundane corpuscles are regarded as elementary entities with no internal structure. This is because the corpuscles must give up momentum to ordinary matter, and if they have no internal energy modes, they must also impart energy to ordinary matter, and this energy will be enormous (considering the high speed of the corpuscles necessary to avoid drag and aberration), sufficient to vaporize all ordinary matter in a fraction of a second.

In an effort to remedy this problem, Kelvin considered (as Fatio had done nearly 200 years before) that perhaps the corpuscles are not elementary entities, but are actually compound systems with internal energy modes of enormous capacity. This idea is problematic for several reasons. First, and most fundamentally, internal energy modes (such as vibration or rotation) require an extremely strong force of attraction to hold the various parts of the corpuscle together, and therefore each distinct part of a corpuscle must act as a center of force, attracting it to the other parts of the corpuscle. Maxwell remarked on this with his characteristically dry wit

Such centres of force are no doubt in their own nature indivisible, but then they are also singly incapable of vibration. To obtain vibrations we must imagine molecules consisting of many such centres, but in doing so the possibility of these centres being separated altogether is again introduced… it is in questionable scientific taste, after using atoms so freely to get rid of forces acting at sensible distances, to make the whole function of the atoms an action at insensible distances.

To put it more bluntly, it is an intellectual sham to pretend to eliminate elementary forces of attraction between distinct entities by invoking a model that relies crucially on elementary forces of attraction between distinct entities. In other words, even if Kelvin’s suggestion was viable (which it isn’t, as discussed below), it wouldn’t accomplish what he intended, which was to explain the apparent force of attraction purely in terms of repulsive contact forces (vis a tergo) without the need for any elementary force of attraction, in accord with the Cartesian notion that all action can be reduced to instances of contact forces. Lesage himself sought to distinguish between attraction and cohesion, the latter being a force tending to hold the contiguous parts of a single entity together. This may have motivated Lesage to envisage ordinary matter as a contiguous lattice structure (“cages”), to avoid the need for attraction between spatially separate matter. However, to endow spatially extended matter with cohesiveness as well as internal dynamics is to embed a field theory within a particle theory. We must then postulate a set of physical laws governing the cohesion (and repulsion) of the elements of a continuous medium, and the forces involved in these laws must be produced by a process that is totally dis-similar to the particle-based mechanism of gravity.

The only other alternative is to opt for the “turtles all the way down” strategy. Suppose that, in order to explain the forces of attraction (or cohesion) holding each compound gravitational corpuscle together, we postulate another radiation field of even finer corpuscles with even greater penetrating power and even greater speeds, producing a “meta-gravity”, thereby accounting for the cohesion of the gravitational corpuscles (and presumably another parallel flux to account for the cohesion of ordinary matter). Of course, we then face the same heat problem for the gravitational corpuscles that we previously faced for ordinary matter, so we must now appeal to a meta-meta-gravity, and so on, ad infinitum. There is some evidence in De Rerum Natura that Lucretius had something like this in mind when he wrote (as translated by William Ellery Leonard)

For thou wilt mark here many a speck, impelled

By viewless blows, to change its little course,

And beaten backwards to return again,

Hither and thither in all directions round.

Lo, all their shifting movement is of old,

From the primeval atoms; for the same

Primordial seeds of things first move of self,

And then those bodies built of unions small

And nearest, as it were, unto the powers

Of the primeval atoms, are stirred up

By impulse of those atoms' unseen blows,

And these thereafter goad the next in size;

Thus motion ascends from the primevals on,

And stage by stage emerges to our sense,

Until those objects also move which we

Can mark in sunbeams, though it not appears

What blows do urge them.

We might also compare this with the modern theory of Brownian motion. However, even if we were prepared to contemplate this infinite hierarchy of radiation fields, with energies increasing to infinity as we rise in the hierarchy, it would not work, because the effective interaction cross-section between two particles is the sum of their radii, so it can never be less than the larger of the two radii, which is that of the particles of ordinary matter. The original ultra-mundane corpuscles are already of negligible size compared with these, so none of the meta-corpuscles can have a lesser interaction cross-section. The only alternative is to postulate zero cross-sections for all particles, and let their interactions be governed by fields with differing coupling strengths. But this again involves force at a distance, the very thing we are supposedly trying to eliminate.

Setting aside the fact that the Fatio-Lesage model, even if it were viable, would not accomplish its intent, we might still wonder whether the Lesagean model is viable on its own terms. As already mentioned, in order to convey a given amount of momentum, a simple particle moving at speed v must lose a specific amount of translational speed, which corresponds to a specific amount of translational kinetic energy. There are several possibilities as to what might become of this enormous quantity of energy, but to even enumerate these possibilities we must agree on a theoretical basis, because the kinetics and dynamics of particles depend on this basis. For example, in Newtonian terms the momentum of a massive particle is mv and the kinetic energy is mv²/2, whereas in special relativity (and any other empirically viable theory of mechanics) the momentum and total mass-energy are mv/[1−(v/c)²]^1/2 and mc²/[1−(v/c)²]^1/2. Furthermore, for an entity moving at the speed c (like an electromagnetic wave) the rest mass is necessarily zero, and the momentum and energy are related by p = E/c. Therefore, according to the empirically viable theories of mechanics and electrodynamics, any conveyance of momentum at the speed of light must be accompanied by a proportional transference of energy. In addition, the drag and aberration associated with a Lesagean flux of speed c would be unacceptably great, so the idea of a light-speed Lesage model is ruled out on three counts (or four, if we include the fact that it wouldn’t dispense with the need for elementary attractive forces even if it did work.).

At this point, a determined Lesagean is faced with a few possible alternatives. He might attempt to proceed based on the premise of corpuscles moving many orders of magnitude faster than light, but then he must also propose an entirely new system of dynamics, including new definitions of momentum and kinetic energy, because the existing definitions are not applicable to particles moving faster than light. (This is true regardless of whether one adopts the Einsteinian or the Lorentzian interpretation of relativity.) But if we are prepared to entertain completely new laws of physics, then the program is self-defeating, because the original intent was to account for gravitational attraction in terms of the ordinary mechanical behavior of material objects. It isn’t clear whether any alternative system of physical laws can be formulated, but even if it could, this would represent the abandonment, not the accomplishment, of the original intent.

The dedicated Lesagean might also try to imagine some way of modifying the Lesage mechanism so that it yields a non-central force to avoid the aberration and drag problems without requiring super-luminal speeds. However, this again would entail completely new physical laws, because the aberration and drag problems correspond directly to basic conservation of momentum for kinetic corpuscles, which supposedly are the basis of the theory. Needless to say, any suggestion that the Lesagean flux undergoes vortex motion, ala Descartes, is completely untenable, not only for all the reasons (e.g., retrograde orbits) that led to the abandonment of the Cartesian system in the first place, but also because it is grossly inconsistent with the Lesagean mechanism itself, which relies on purely rectilinear paths and non-interacting corpuscles, at least on the scale over which the force of gravity varies inversely as the square of the distance.

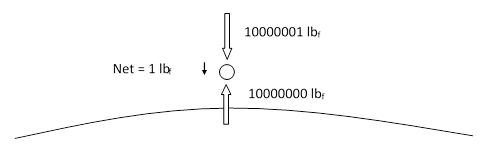
Many other considerations undermine the viability of the Fatio-Lesage model of gravity. For example, from the absence of any appreciable shielding effect for gravity, we know that the difference between the upward and downward flux at the earth’s surface can be no greater than 1 part in 10⁷, and therefore the apparent force of 1 pound on a small mass near the Earth’s surface is actually just the difference between two gigantic opposing forces, as indicated in the figure below.

This has several important implications. First, it implies that the ultra-mundane flux arriving from opposite regions of the universe must be incredibly isotropic. Suppose for example that the ultra-mundane flux had the same degree of isotropy as the cosmic microwave background radiation, which is about 1 part in 10⁵.  This is extremely isotropic by most standards (in fact, it’s so isotropic that some process like cosmic inflation seems necessary to account for it), and yet this degree of isotropy would cause fluctuations in the “weight” of a 1 pound object (in the shape of a slender rod, to make it sensitive to the directional flux) on the order of 100 pounds. This conflicts grossly with the empirical uniformity in the weight of objects at different locations and orientations near the Earth’s surface. Hence the ultra-mundane flux must not only travel many orders of magnitude faster than the speed of light, it must also be many orders of magnitude more isotropic than any known field. (This entails an incredible uniformity not only of the speed and intensity of the particle rays, but also of the directions.) Since the particles arriving here at any given moment have come from distant regions of space in opposite directions at speeds far in excess of the speed of light, it’s clear that they have had no chance to interact with each other prior to their arrival, so we cannot explain the phenomenal uniformity other than by calling it a perpetual miracle.

Another implication concerns the expenditure of work. According to the usual way of thinking, when a 1 lb object falls through a distance of 1 foot, the “force of gravity” has performed 1 ft-lb of work on the object, converting potential energy into kinetic energy. However, according to the Fatio-Lesage model, the downward flux has performed 10000001 ft-lbs of work on the object, which in turn has performed 10000000 ft-lbs of work on the upward flux. The net work on the object is still just 1 ft-lb, but this has been accomplished only by the fantastically precise balance of two enormous expenditures of work, and nearly all of this excess effort must be degraded into non-translational forms of energy. As a result, there is a gigantic production of entropy, and it should be noted that this applies just as much to Kelvin’s model (with corpuscles able to absorb energy) as it does to the basic Fatio-Lesage model. In either case, the energy must be absorbed in non-coherent vibration or rotation, with the corresponding increase in entropy. In fact, this applies even if the macroscopic object is stationary. The mere production of 1 pound of force, in the Fatio-Lesage model, involves an almost unimaginable rate of entropy production in the ultra-mundane flux.  Hence, processes that we are used to regarding as isentropic, such as the motions of planets in their orbits, are actually (according to Fatio-Lesage) tremendously non-isentropic. The concept of entropy as distinct from energy was still being developed and clarified in Maxwell’s day, but these were clearly the considerations that Maxwell had in mind when he wrote (in an encyclopedia article on the Atom)

We may also observe that according to this theory the habitable universe, which we are accustomed to regard as the scene of a magnificent illustration of the conservation of energy as the fundamental principle of all nature, is in reality maintained in working order only by an enormous expenditure of external power, which would be nothing less than ruinous if the supply were drawn from anywhere else than from the infinitude of space, and which, if the contrivances of the most eminent mathematicians should be found in any respect defective, might at any moment tear the whole universe atom from atom.

Still another implication concerns Kelvin’s suggestion that the “spent” corpuscles, after interacting with ordinary matter and acquiring an enormous amount of internal energy (with corresponding loss of translational energy), could be restored to their former condition by mingling with fresh corpuscles in the far reaches of space. (As Maxwell dryly put it, Kelvin “has also suggested the possibility of the vortex corpuscle regaining its swiftness and losing part of its vibratory agitation by communion with its kindred corpuscles in the infinitude of space”.) Clearly this suggestion is untenable, because it entails a reduction in the overall entropy of the universe, countering the production of entropy resulting from the creation of gravitational force. Of course, if we posit an infinite universe with only a finite amount of mass, then the spent corpuscles might asymptotically approach their original condition, but in that case it’s irrelevant, because the matter in the habitable universe would forever be bombarded with fresh corpuscles of low entropy from the infinite ultra-mundane regions. But in any universe where there is a finite ratio of ordinary matter to ultra-mundane corpuscles, the entropy must continually increase.

Maxwell actually repeated this criticism of the Fatio-Lesage concept many times, so he apparently regarded it as the most damning (speaking at a time prior to the recognition of the relativistic aspects of dynamics). For example, in his review of Challis’ Essay on the Mathematical Principles of Physics he wrote

…in whatever way we regard Lesage’s theory [including Kelvin’s variant], the cause of gravitation in the universe can be represented only as depending on an ever fresh supply of something from without… the universe is not even temporarily automatic, but must be fed from moment to moment by an agency external to itself… if the corpuscles were from any cause to be supplied at a different rate, the value of every force in the universe would suffer change…  the preservation of the universe is effected only by the unceasing expenditure of enormous quantities of work, so that the conservation of energy in physical operations, which has been the subject of so many measurements, and study of which has led to so many discoveries, is apparent only, and is merely a kind of “moveable equilibrium” between supply and destruction.

Likewise in his encyclopedia article on Attraction he wrote in regard to Lesage’s theory

It is remarkable that of the… hypotheses which go some way towards a physical explanation of gravitation, every one involves a constant expenditure of work… According to such hypotheses we must regard the processes of nature not as illustrations of the great principle of the conservation of energy, but as instances in which, by a nice adjustment of powerful agencies not subject to this principle, an apparent conservation of energy is maintained. Hence we are forced to conclude that the explanation of the cause of gravitation is not to be found in any of these hypotheses.

In 1905 G. H. Darwin published a paper entitled “The Analogy between Lesage’s Theory of Gravitation and the Repulsion of Light”, in which he derived expressions for the forces of attraction and drag and for the energy transfer in Lesage’s theory, based on the assumption of spherical particles as the elementary opaque entities from which macroscopic bodies are composed. He allowed for differing amounts of elasticity in the normal and tangential directions, but he neglected the effects of secondary impacts of reflected particles. His main conclusions were that the mutual forces of attraction between bodies would be equal and opposite only if all the elementary particles are of exactly the same size, and that the force is perfectly proportional to the inverse square of the distance only if the gravific corpuscles are perfectly inelastic (i.e., are totally absorbed when they strike ordinary matter). He points out that, on this basis, the theory “demands a continual creation of energy at infinity to supply the gravific machinery”, which like Maxwell he regards as “a fundamental objection to the physical truth of Lesage’s hypothesis”.

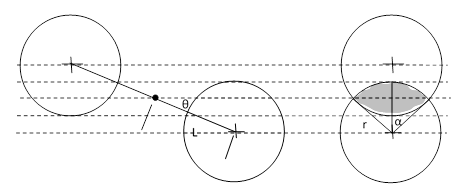
Darwin’s analysis is quite complicated, mainly because he allows for unequal particle sizes with variable amounts of normal and tangential elasticity. It’s easy to see that, in order for the strict proportionality between inertial and gravitational mass to hold good, the elementary opaque molecules of which macroscopic bodies are composed must be identical spheres, because otherwise the force of gravity would depend on the orientation of an object, and also the ratio of opaque area to inertial mass would differ from one object to another. (Admittedly it’s conceivable that multiple distinct types of molecules could exist, but they would all need to occur in fixed proportions and be arranged isotropically in all substances, which is rather implausible.) It can also be shown directly that the mutual force of gravitational attraction between two bodies would be equal and opposite only in the case of total absorption (zero reflection) of the gravific corpuscles. With these two assumptions (equal sized spherical particles and total absorption), it’s not too difficult to show that the force of attraction is precisely proportional to the inverse square of the distance. To see this, consider the two spherical particles illustrated below.

Every ray through the space contains gravific corpuscles moving in both directions, but only the rays that pass through both spheres contribute to the unbalanced forces. One way of parameterizing the omni-directional flux is to consider the set of parallel rays all pointing in one particular direction, so each direction in space corresponds to a family of rays, or rather, a density of rays, because it’s necessary to integrate the density over some non-zero solid angle to give actual rays. (This is one of the peculiar features of the concept of an omni-directional flux in the continuous limit: the probability of finding a ray in any specific direction are zero. There is a non-zero probability of finding a ray only over a non-zero range of directions.)  Also, by symmetry, it’s clear that only net imbalance will be along the axis between the spheres. Hence we can determine the net force on the spheres by integrating their common projected areas over all directions in space, and multiplying each of these contributions by the cosine of the angle θ between the axis and the respective ray direction. The projected common area for any given θ is easily seen to be

The first term inside the brackets on the right is the area of the sector swept out by the angle 2α, and the second term is the area of the triangle cut by the mid-chord. The force density at this angle is proportional to this area, so we then need to integrate this as θ varies from 0 to invsin(r/L), and at each of those angles we rotate the figure about the x axis through the angle ϕ = 0 to 2π, which means we need to scale by sin(θ). Also, we apply the scale factor of cos(θ) to take just the projection along the axis between the spheres. Thus the total force is proportional to the integral

Evaluating the integral gives the normalized result πr⁴/(2R²) where R = 2L is the distance between the centers of the spheres. To get the actual force, we must evaluate the double-integral of the integrand in the above expression multiplied by ρv² dθ dϕ / 4π, where ϕ is evaluated from 0 to 2π. Note that the quantity

is the fraction of the total flux per unit area moving in the directions contained within the angular increments dθ and dϕ. Thus the force is given by

This is identical to the result found by Darwin for the special case of total absorption and particles of equal size.

Following Darwin, Poincare discussed Lesage’s theory in his 1908 book Science and Method. Unfortunately his analysis as presented there appears to be badly garbled. It’s helpful to begin by describing what Poincare presumably intended to say, and then review how his published explanation has been garbled. He considers first the case of totally inelastic corpuscles. According to Le Sage theory, any macroscopic body is composed of elementary opaque particles with a total cross-sectional area S (which for the ordinary matter of our experience is very much less than the macroscopic cross-section of the body). This total opaque cross-section must be essentially the same in all directions, because the weight of a body doesn’t depend on its orientation. Also, the mass m of a body must always be proportional to the opaque projected area S, so there is a universal constant λ such that m = λS for all non-saturated bodies (which includes all matter of which we have any experience).

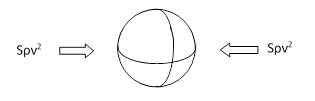
If a macroscopic material globe of opaque area S is immersed in a flux of particles with density ρ and average speed v, and all the particles that strike the body are absorbed, the pressure exerted by the flux on the opaque surfaces of the globe is ρv²/3, so the total force exerted on each side of the globe is on the order of Sρv². Since this same pressure is applied in both directions, the net force on the globe is zero, as illustrated in the figure below.

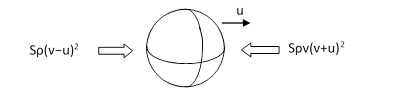
Now suppose the globe is moving to the right with the constant speed u relative to isotropic frame of the flux, as illustrated in the figure below.

The relative speed of particles impinging on the globe is v – u from the left and v + u from the right. Consequently the forces on the two sides are on the order of Sρ(v−u)² and Sρ(v+u)², so the globe experiences a net drag of magnitude

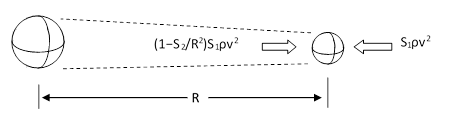
Lastly, consider two stationary globes, with opaque projected areas S₁ and S₂, located at a distance R from each other, as shown in the figure below.

The total area at a distance R from the right hand globe is proportional to R², and the blocked area is S₂, so the flux striking the right globe from the left is reduced by a factor of (1−S₂/R²) due to the presence of left globe. Hence the right globe is subjected to a net force in the direction of the left globe, and the magnitude of this net force is

It follows that Newton’s gravitational constant in this theory is G = (v/λ)²ρ. If the right hand globe is in a circular orbit around the left hand globe, assumed to be at rest in the balanced (isotropic) frame of the flux, then it is moving with some speed u (perpendicular to F) relative to the isotropic frame. Hence it is subjected to a drag force on the order of S₁ρvu, and the ratio of this drag force to the force of attraction is

Re-arranging this and substituting m₂/λ for S₂ gives us an expression for the flux velocity

If we take Globe 1 to be the Moon, and Globe 2 to be the Earth, then R = (3.8)10⁸ m is the distance from the Earth to the Moon, u = 953 m/sec is the Moon’s orbital speed, and m₂ is the Earth’s mass. To determine a lower bound on the universal constant λ, recall that Laplace calculated that the Earth cannot reduce the strength of gravity by more than 1 part in ten million, so S₂ is no greater than 10^-7 times the Earth’s macroscopic cross-section, which is on the order of r_e² where r_e = (6.4)10⁶ m is the radius of the Earth. Thus we have

As for the ratio D/F, we know from extremely precise observations of the Moon over many years that if there is any drag at all on the Moon it must be incredibly slight. These observations enable us to say that D/F for the Moon is no greater than (2)10^-13. Combining all this information, the above equation implies that the speed v of the flux can be no less than (7.1)10²⁶ m/sec, which is (2.4)10¹⁸ times the speed of light.

The kinetic energy imparted to the Earth (Globe 2) per second is on the order of v times the integrated force to which it is subjected over its entire surface S₂ (because all the kinetic energies of the particles striking this surface are absorbed), so we have

Inserting the values (or lower bounds) for each of these parameters, we find that the Earth is absorbing at least (4.2)10⁵⁹ Joules per second. For comparison, the Sun’s entire rate of energy output (not just the portion reaching Earth, but the entire energy output of the Sun) is (4)10²⁶ Joules per second, so according to Le Sage’s theory the Earth must be absorbing energy from the ultramundane flux at a rate that is at least 10³³ times the Sun’s output.

We could summarize the expressions (order of magnitude) for the drag, attraction, and energy rate as follows:

Turning now to Poincare’s actual text, he asserts that

The attraction exercised by the earth upon a mass 1 at a distance 1 will then be proportional both to S, the total surface of the spherical molecules of which it is composed, to v, the velocity of the corpuscles, and to the square root of ρ, the density of the medium formed by the corpuscles. The heat produced will be proportional to S, to the density ρ, and to the cube of the velocity v. The calculated resistance is proportional to S, to ρ, and to v. Now we know that the heavenly bodies move as if they met with no resistance, and the precision of the observations enables us to assign a limit to the resistance. This resistance varying as Sρv, while the attraction varies as Svρ^1/2 we see that the relation of the resistance to the square of the attraction is in inverse ratio of the product Sv. We get thus an inferior limit for the product Sv. We had already a superior limit for S (by the absorption of the attraction by the bodies it traverses). We thus get an inferior limit for the velocity v, which must be at least equal to (24)10¹⁷ times the velocity of light. From this we can deduce ρ and the amount of heat produced.

At least one English edition (2001 Modern Library Paperback Edition) of Science and Method replaces the Greek symbol ρ with the letter p, and applies the square root to v as well as ρ in the symbolic expression for the attraction, contrary to Poincare’s verbal description. We can attribute these to simple typos. Setting these aside, we see that Poincare’s assessment of the rate of heat production is perfectly consistent with our expression for dE/dt, and his estimate of the “resistance” is indeed proportional to our expression for the drag experienced by a body moving at a given speed u. However, Poincare’s prescription for the force of attraction is rather puzzling. For a unit distance R = 1, he says the attraction is proportional to the square root of our expression for the force of attraction. But then he squares his so-called “attraction” before taking the ratio to the resistance. Hence he gets the same ratio as we did, but he calls it the ratio of the squared attraction divided by the resistance, whereas according to our analysis he is simply forming the dimensionless ratio of the attraction divided by the resistance. This all applies for a given speed u, which Poincare never mentions (even though he remembers to stipulate a unit mass and unit distance). In summary, Poincare employs the following expressions for the resistance (drag), attraction, and energy rate:

These three quantities are identical to what is inside the parentheses of the previous expressions, so they are consistent except for the puzzling claim that the attraction is proportional to the square root of S²ρv². Remember that these expressions are just proportionalities, not equalities or approximations, so there is really an undetermined factor k multiplying each of them. Of course, if Poincare divided F by D, this unknown factor would cancel out, so it would not be a concern, but he actually divides F² by D, so the ratio is not Sv but rather kSv, and hence he would not be able to infer the value of v (which he claims to do) without knowing the value of k. All of this suggests that something in Poincare’s published analysis was garbled. At best, his reasoning is unclear.

From this point Poincare notes that the observed stability of the lunar orbit implies the ratio of the squared (sic) force of gravity to the drag force must be very great, so this places a lower limit on the product Sv (neglecting the extra power of the constant of proportionality).  Also, the lack of absorption (shielding) placed an upper limit on S (the opaque area of a unit mass), so together these imply a lower limit on v. By this reasoning, Poincare concludes that v must be at least (24)10¹⁷ times the speed of light. Inserting this along with the upper bound on S into the equation for the attractive force, he determines the flux density ρ, and then he computes the energy transferred to the object. He finds that the Earth would receive an amount of heat at a rate equal to 10²⁰ times the Sun’s entire energy output rate. Oddly enough, this is exactly what our previous analysis would have given if we have omitted the factor F/D from the expression for v. In the expression dE/dt = Gλmv the only value not explicitly stated by Poincare is λ, but it is hard to imagine that he was using a value for this parameter that differs by 13 orders of magnitude from our value.

Return to MathPages Main Menu