Huygens' Principle

In 1678 the great Dutch physicist Christian Huygens (1629-1695) wrote a treatise called Traite de la Lumiere on the wave theory of light, and in this work he stated that the wavefront of a propagating wave of light at any instant conforms to the envelope of spherical wavelets emanating from every point on the wavefront at the prior instant (with the understanding that the wavelets have the same speed as the overall wave). An illustration of this idea, now known as Huygens' Principle, is shown below.

This drawing depicts the propagation of the wave “front”, but Huygens’ Principle is understood to apply equally to any locus of constant phase (not just the leading edge of the disturbance), all propagating at the same characteristic wave speed. This implies that a wave doesn't get "thicker" as it propagates, i.e., there is no diffusion of waves. For example, if we turn on a light bulb for one second, someone viewing the bulb from a mile away will see it "on" for precisely one second, and no longer. Similarly, the fact that we see sharp images of distant stars and galaxies is due to Huygens’ Principle. However, it’s worth noting that this principle is valid only in spaces with an odd number of dimensions. (See below for a detailed explanation of why this is so.) If we drop a pebble in a calm pond, a circular wave on the two-dimensional surface of the pond will emanate outward, and if Huygens' Principle was valid in two dimensions, we would expect the surface of the pond to be perfectly quiet both outside and inside the expanding spherical wave. But in fact the surface of the pond inside the expanding wave (in this two-dimensional space) is not perfectly calm, its state continues to differ slightly from its quiescent state even after the main wave has passed through. This excited state will persist indefinitely, although the magnitude rapidly becomes extremely small. The same occurs in a space with any even number of dimensions. Of course, the leading edge of a wave always propagates at the characteristic speed c, regardless of whether Huygens' Principle is true or not. In a sense, Huygens' Principle is more significant for what it says about what happens behind the leading edge of the disturbance. Essentially it just says that all the phases propagate at the same speed.

From this simple principle Huygens was able to derive the laws of reflection and refraction, but the principle is deficient in that it fails to account for the directionality of the wave propagation in time, i.e., it doesn't explain why the wave front at time t + Dt in the above figure is the upper rather than the lower envelope of the secondary wavelets. Why does an expanding spherical wave continue to expand outward from its source, rather than re-converging inward back toward the source?  Also, the principle originally stated by Huygens does not account for diffraction. Subsequently, Augustin Fresnel (1788-1827) elaborated on Huygens' Principle by stating that the amplitude of the wave at any given point equals the superposition of the amplitudes of all the secondary wavelets at that point (with the understanding that the wavelets have the same frequency as the original wave). The Huygens-Fresnel Principle is adequate to account for a wide range of optical phenomena, and it was later shown by Gustav Kirchoff (1824-1887) how this principle can be deduced from Maxwell's equations. Nevertheless (and despite statements to the contrary in the literature), it does not actually resolve the question about "backward" propagation of waves, because Maxwell's equations themselves theoretically allow for advanced as well as retarded potentials. It's customary to simply discount the advanced waves as "unrealistic", and to treat the retarded wave as if it was the unique solution, although there have occasionally been interesting proposals, such as the Feynman-Wheeler theory, that make use of both solutions.

Incidentally, as an undergraduate, Feynman gave a seminar on this "new idea" at Princeton. Among the several "monster minds" (as Feynman called them) in attendance was Einstein, to whom the idea was not so new, because 30 years earlier Einstein had debated the significance of the advanced potentials with Walther Ritz. In any case, the Huygens-Fresnel Principle has been very useful and influential in the field of optics, although there is a wide range of opinion as to its scientific merit. Many people regard it as a truly inspired insight, and a fore-runner of modern quantum electro-dynamics, whereas others dismiss it as nothing more than a naive guess that sometimes happens to work. For example, Melvin Schwartz wrote that to consider each point on a wavefront as a new source of radiation, and to add the radiation from all the new sources together, “makes no sense at all”, since (he argues) “light does not emit light; only accelerating charges emit light”. He concludes that Huygens’ principle “actually does give the right answer” but “for the wrong reasons”. However, Schwartz was expressing the classical (i.e., late 19th century) view of electromagnetism. The propagation of light in quantum field theory actually is consistent with the very interpretation of Huygens’ principle that Schwartz regarded as nonsense.

Whether we have now actually found the true "reason" for the behavior of light is debatable, and ultimately every theory is based on some fundamental principle(s), but it's interesting how widely the opinions on various principles differ. (I'm reminded of the history of Fermat's Principle, and of Planck's reverence for the Principle of Least Action.) It could be argued that the “path integral” approach to quantum field theory – according to which every trajectory through every point in space is treated equivalently as part of a possible path of the system – is an expression of Huygens’ Principle. It’s also worth reflecting on the fact that the quantum concept of a photon necessitates Huygens’ Principle, so evidently quantum mechanics can work only in space with an odd number of dimensions.

Setting aside these weighty considerations, it's interesting to review the mathematical content of Huygens' original principle. The usual wave equation for a scalar field ψ(x₁,x₂,..,x_n,t) in n space and 1 time dimension is

(We've chosen units of time and space so that the wave velocity is 1.) If we consider a spherically symmetrical wave we have ψ = ψ(r,t) where

For future reference, notice that

for every index j from 1 to n. It follows that

Returning to the basic wave equation, and assuming ψ is strictly a function of r and t, we have the following partial derivatives with respect to each of the space variables:

Since partial differentiation is commutative, the second factor in the last term of the right- hand equation can be written as

Now, since

the preceding mixed partial is simply

Substituting back into the expression for the second partial derivative of ψ with respect to x_j, we have

Summing all these partials for j = 1 to n gives

Hence the spherically symmetrical wave equation in n spatial dimensions can be written as

Now suppose we define a new scalar field by the relation ϕ(r,t) = r^k ψ(r,t) where k is some fixed constant. The partial derivative of this scalar field with respect to r are

Notice that if we set k = (n–1)/2, and if we divide through this second partial by r^k, we have

This is nearly the same as the left-hand side of the spherically symmetrical wave equation, except for the last term. Hence we can write the wave equation in the form

Furthermore, we can multiply through by r^k = r^(n–1)/2 to put this in the equivalent form

If n equals 1, meaning that we have just a single space dimension, then r = x₁ and ϕ = ψ, so we expect the second term on the left hand side to vanish identically, as indeed it does, leaving us with just the original one-dimensional wave equation, with the well-known general solution

for arbitrary functions f and g. However, we might not have anticipated that the second term in the transformed wave equation also vanishes if n equals 3, i.e., in the case of three spatial dimensions. In this case the spherically symmetrical wave equation once again reduces to a one-dimensional wave equation, although in the modified wave function ϕ = rψ. Hence the general solution in three space dimensions is

The fact that this solution is divided by r signifies that the magnitude of the wave tends to drop as r increases (unlike the one-dimensional case, in which a wave would theoretical propagate forever with undiminished strength).  Focusing on just the "retarded" component of the wave, f(r–t)/r, the fact that the time parameter t appears only in the difference r–t implies that the (attenuated) wave propagates in time with a phase velocity of precisely 1, because for any fixed phase β we have r–t = β and so dr/dt for this phase point is 1. Consequently if f is a single pulse, it will propagate outward in a spherical shell at precisely the speed 1, i.e., on the light cone. Conversely, it can be shown that the wave function at any point in space and time is fully determined by the values and derivatives of that function on the past light cone of the point. Any wave equation for which this is true (i.e., for which disturbances propagate at a single precise speed) is said to satisfy Huygens' Principle. The connection with Huygens' original statement about secondary wavelets is that each wavelet - with the same speed as the original wave - represents a tiny light cone at that point, and Huygens' principle asserts that light is confined to those light cones.

It's worth noting that in the above derivation we were able to reduce the polar wave equation to a simple one-dimensional equation by taking advantage of the fact that an unwanted term vanished when the number of space dimensions is n = 3 (or n = 1). For the case of two dimensional space this doesn't work (nor would it work with four space dimensions). We can still solve the wave equation, but the solution is not just a simple spherical wave propagating with unit velocity. Instead, we find that there are effectively infinitely many velocities, in the sense that a single pulse disturbance at the origin will propagate outward on infinitely many "light cones" (and sub-cones) with speeds ranging from the maximum down to zero. Hence if we lived in a universe with two spatial dimensions (instead of three), an observer at a fixed location from the origin of a single pulse would "see" an initial flash but then the disturbance "afterglow" would persist, becoming less and less intense, but continuing forever, as slower and slower subsidiary branches arrive. (It's interesting to compare and contrast this "afterglow" with the cosmic microwave background radiation that we actually do observe in our 3+1 dimensional universe. Could this glow be interpreted as evidence of an additional, perhaps compactified, spatial dimension? What would be the spectrum of the glow in a non-Huygensian universe? Does curvature of the spatial manifold affect Huygens’ principle?)

It turns out that Huygens' Principle applies only with one time dimension and n = 3, 5, 7.., or any odd number of space dimensions, but not for any even number of space dimensions. (The case n = 1 is degenerate, because a pulse has only one path to take.) To see why, let's return to the general spherically symmetrical wave equation in n space dimensions

and consider a solution of the form ψ(r,t) = f(r)g(t). (Naturally not all solutions are separable in this way, but since the wave equation is linear, we can construct more general solutions by summing a sufficient number of solutions of the separable form f(r)g(t).) Inserting this into the wave equation and expanding the derivatives by the product rule gives

Dividing through by fg gives

Notice that the left hand side is strictly a function of r, and the right hand side is strictly a function of t. Since r and t are independent variables, the left and right sides must both equal a constant, which we will denote by κ. Hence we have two separate ordinary differential equations

If κ is positive or zero the right hand equation gives “run-away” solutions for g(t), whereas if κ is negative we can choose scaling so that κ = –1 and then g(t) satisfies the simple harmonic equation, whose solutions include functions of the form sin(ct) and cos(ct). The left hand equation can be re-written in the form

If we multiplied this through by r, it would be in the form of what is called Bessel's equation, named after Friedrich Wilhelm Bessel (1784-1846), the German astronomer who (incidentally) was the first person to determine the distance to a star (other than the Sun). In 1838 he determined the distance to the star called "61 Cygni" based on the parallax as viewed from the Earth at six-month intervals. Bessel functions are solutions of a standard Bessel equation, just as the ordinary trigonometric functions, sine and cosine, are solutions of the differential equation y" + y = 0.

To solve the above equation we can assume a series solution of the form

for some integer q (which may be positive, negative, or zero) such that c₀ is non-zero. The derivatives of this function are

Substituting these into the differential equation, and collecting terms by powers of r, we get

The coefficient of each power of r must vanish, and since c₀ is non-zero, the expression for the first coefficient implies q(q – 2 + n) = 0. This is called the indicial equation, because it determines the acceptable value(s) of q. In this case we must have either q = 0 or else q = 2 – n. If q = 0 then the coefficient of r^q equals c₁(n–1), so either n = 1 or else c₁ = 0. On the other hand, if q = 2 – n, then the coefficient of r^q equals c₁(3–n), so either n = 3 or else again c₁ = 0. We've already seen that the original differential equation has a particularly simple analytical solution when n (the number of space dimensions) equals either 1 or 3, so we need not consider them here. For all other value of n, we must have c₁ = 0. (Of course, even with n = 1 or 3, we are free to set c₁ = 0.)

Now, examining the coefficients of the higher powers of r, we see that in general the coefficient of r^q+m is of the form

Inserting q = 0, setting the overall coefficient to zero, and solving for c_m+1 gives

for m = 0, 1, 2,... Since c₀ is, by definition, the first non-zero coefficient, it follows that c–1 is zero, and therefore c₁ = 0. Moreover, applying the above formula recursively, we see that all the c_j coefficients for odd indices j must vanish. On the other hand, the coefficients with even indices are given recursively by

and so on. Notice that if n = 1 the denominators are 1·2, 3·4, 5·6, ..., etc., so the general non-zero coefficient of the solution can be written simply as

giving the solution

Hence the solution is simply f(r) = c₀ cos(r). Recall that g(t) has solutions of the form cos(ct) and sin(ct), and we can create a solution given by the sum of two separable solutions, so, for example, one solution is

Similarly if n = 3 the denominators of the recursive formulas are 2·3, 4·5, 6·7, ..., etc., so the general non-zero coefficient is

giving the solution

so in this case we have f(r) = c₀ sin(r)/r. Combining this with suitable solutions for g(t) as in the case of n = 1, we can arrive at overall solutions such as ψ(r,t) = cos(r–ct)/r. This shows (again) that the cases of 1 and 3 spatial dimensions lead to especially simple solutions.

In general, for arbitrary positive integer n, the coefficient c_2j is of the form

Notice that for n = 1 the factors in the square brackets are consecutive odd integers, and they can be interleaved between the consecutive even integers to give a pure factorial product. Likewise for n = 3 the odd and even factors can be interleaved to give a pure factorial product. For higher odd integers we can interleave the factors in the same way, although there will be a fixed number of leading even factors and the same number of trailing odd factors that don't overlap. For example, with n = 7 the coefficient c₁₂ is as shown below, after re-arranging the six even and six odd factors in the denominator

Taking advantage of this interleaving, we can express the general coefficient (for sufficiently large j) with odd n > 3 in the form

For any fixed n, the first factor on the right is just a constant, and the second factor is just one over a polynomial of degree (n–3)/2 in the index j. Therefore, after some number of terms, the series solution goes over to a simple factorial form with a polynomial divisor. It can be shown that the resulting function f(r) is such that Huygens' Principle is satisfied, so this implies that the principle is satisfied for any odd number of space dimensions. (See the note on Spherical Waves in Higher Dimensions.)

In contrast, if the number of space dimensions is even, we do not have interleaving of the factors in the denominator of the coefficients. In this case we can only re-write (1) in the form

For example, in the case n = 2 (i.e., two spatial dimensions) we have the coefficients

This gives the function

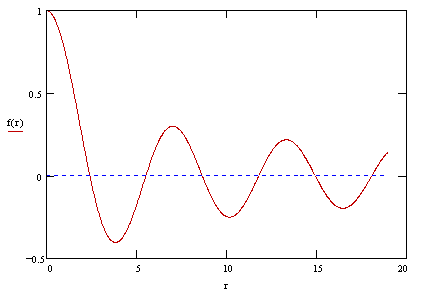
This is the Bessel function of order zero, often denoted as J₀. A plot of this function is shown below.

For positive arguments r, the Bessel function J₀(r) can be expressed as

Multiplying through by the temporal solution g(t) = sin(ct) gives

Hence, instead of the solution being purely a function of r ± ct as in the case of odd dimensions, we find that it is an integral of functions of cosh(θ)r ± ct. Each value of θ corresponds to a propagation speed of c/cosh(θ), so the speeds vary from c down to zero. This signifies that the wave function at any event is correlated not just with the wave function on its “light cone”, but with the wave function at every event inside its light cone. (However, as discussed in another note, we must be cautious about inferring causality relations from such formulas.)

It would be interesting to work out the connections between Huygens' Principle and the zeta function (whose value can only be given in simple closed form for even arguments) and the Bernoulli numbers (which are non-zero only for even indices). It's also interesting to note the analogy between Huygens' spherical wavelets centered on the boundary of the wave front and the technique of analytic continuation, by which we expand the boundary of an analytic region by means of disks of convergence centered on or near the boundary of the existing analytic region.

Paul Dirac (1902-1984) gave an interesting general argument for a much stronger version of Huygens' Principle in the context of quantum mechanics. In his "Principles of Quantum Mechanics" he noted that a measurement of a component of the instantaneous velocity of a free electron must give the value ±c, which implies that electrons (and massive particles in general) always propagate along null intervals, i.e., on the local light cone. At first this may seem to contradict the fact that we observe massive objects to move at speeds much less than the speed of light, but Dirac points out that observed velocities are always average velocities over appreciable time intervals, whereas the equations of motion of the particle show that its velocity oscillates between +c and -c in such a way that the mean value agrees with the average value. He argues that this must be the case in any relativistic theory that incorporates the uncertainty principle, because in order to measure the velocity of a particle we must measure its position at two different times, and then divide the change in position by the elapsed time. To approximate as closely as possible to the instantaneous velocity, the time interval must go to zero, which implies that the position measurements must approach infinite precision. However, according to the uncertainty principle, the extreme precision of the position measurement implies an approach to infinite indeterminacy in the momentum, which means that almost all values of momentum - from zero to infinity - become equally probable. Hence the momentum is almost certainly infinite, which corresponds to a speed of ±c. This is obviously a very general argument, and applies to all massive particles (not just fermions).

Return to MathPages Main Menu