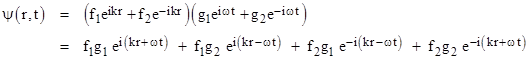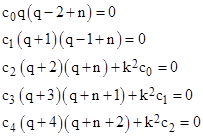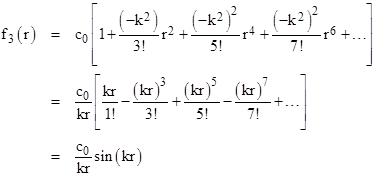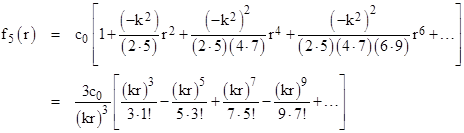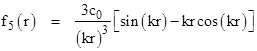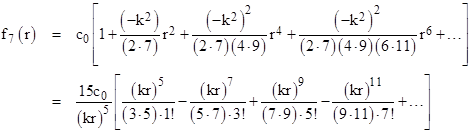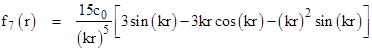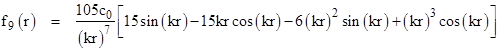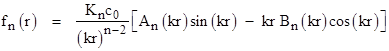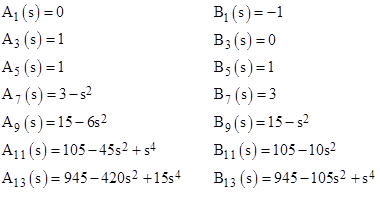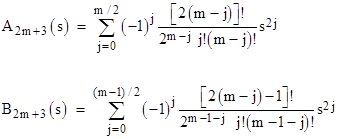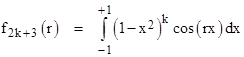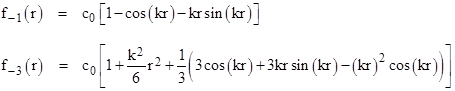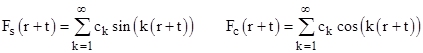Spherical Waves in Higher Dimensions

As discussed in the note on Huygens’ Principle, if we separate the solution ψ(r,t) of the usual wave equation in n-dimensional space (with one time dimension) into a time component and a spatial component, we have ψ(r,t) = f(r)g(t), and the spatial and temporal components satisfy the individual equations

where k is a constant with units of 1/distance and ω is a constant with units of 1/time. Thus the temporal component satisfies the simple harmonic equation, with a general solution of the form g(t) = g₁ e^iωt + g₂ e^–iωt where g₁ and g₂ are arbitrary constants. In just one spatial dimension (n = 1) the spatial equation also reduces to the simple harmonic equation, with the general solution f(r) = f₁ e^ikr + f₂ e^–ikr for constants f₁ and f₂. Combining these, we get the wave function

Thus the solution is a sum of functions of the quantities kr + ωt and kr – ωt. If we require that f and g are real-valued, then g(t) = g₁ cos(wt), f(r) = f₁ cos(kr), and

More generally, we can verify by direct substitution that the one-dimensional wave equation is satisfied by any function of the form

where A(x) and B(x) are quite arbitrary functions. In effect, Huygens’ Principle can be read directly from this equation, since it implies that a pulse disturbance propagates sharply at a constant speed. We also know that with three spatial dimensions (n = 3) the general spatial solution is f(r) = cos(kr)/r, and again Huygens’ principle applies. We asserted that a similar result obtains for any odd number of spatial dimensions. To show this more explicitly, recall that spatial equation is

We assume f(r) has a power series expansion

where c0 is the first non-zero coefficient and q is non-negative (to ensure that f(r) is finite at r = 0). Inserting this series and its derivatives into equation (1) and setting the coefficient of each power of r to zero, we get the conditions

and so on. Since c₀ is stipulated to be non-zero, and since we are requiring q to be non-negative, the first of these conditions implies q = 0, and so the second implies c₁ = 0. The remaining conditions give c_j + 2 as a multiple of c_j, so it follows that c_j = 0 for all odd j. The coefficients with even indices are then given by

With n = 3 the spatial component of the wave function is therefore

On the other hand, in a five-dimensional space, we have n = 5, and the spatial part of the wave function is

Putting s = kr and letting α(s) denote the expression inside the last square brackets, we see that

Multiplying through by s and integrating, we find that α(s) = sin(s) – s cos(s), so we have

The same general approach allows us to determine the closed-form expression for f_n(r) for any odd number of dimensions n. For example, in seven spatial dimensions (n = 7) we have the series

Again putting s = kr and letting α(s) denote the expression inside the last square brackets, we see that

Multiplying and integrating twice gives

Therefore, the spatial part of the spherical solution of the wave equation in seven space dimensions is

The same approach leads to the solution in nine space dimensions

and so on. In general, the spatial part of the spherical wave solution in n dimensions has the form

where the constant K_n equals (n–2)(n–4)…(1), and the expressions A_n(kr) and B_n(kr) denote “even” polynomials in kr. These polynomials for the first several odd values of n are listed below.

In general, for odd n greater than 1, these polynomials can be expressed as

Interestingly, referring to the article on proving that π is irrational, we see that the spatial functions f_n(r) for odd integers n greater than 1 can also be expressed (up to a constant factor) as a simple integral

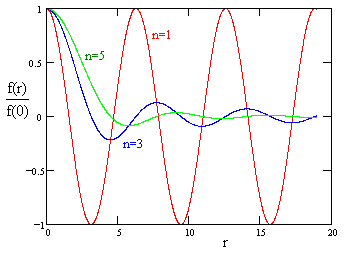
The figure below shows f_n(r) for spaces of one, three, and five dimensions.

Of course, these are just the elementary solutions. We can use linear combinations of solutions of this form to generate arbitrary wave forms.

As an aside, although the case of negative n presumably has no physical significance (negative dimensions?), we note that a similar approach enables us to solve equation (1) for these cases as well. If n is even, the coefficients are undefined (because they involve a division by zero), but we get well-defined functions for odd n. The solutions for the first couple of odd negative values of n are

These solutions increase to infinity as r increases, unlike the solutions for positive n, which drop to zero as r increases.

Returning to positive dimensions, there’s an interesting relationship between the “basis functions” of the general spherical wave solutions in successive odd dimensions. The wave equation in spherical coordinates in n-dimensional space can be written in terms of the differential operator

A function ψ(r,t) is a solution of the n-dimensional wave equation if and only if

Knowing the general form of the spatial part f_n(r), and the simple temporal part for all n, we can write a basic combined space-time solution for odd n as

where A_n(r) and B_n(r) are the polynomials defined previously. By direct substitution it can be verified that successive odd basis solutions are related by

This is a remarkable fact, signifying that a basis solution for n space dimensions not only satisfies the wave equation everywhere in n-dimensional space, it also satisfies the wave equation in spaces of every odd number of dimensions at every radius and time for which the basis solution for n+2 dimensions vanishes. Hence there is an infinite sequence of expanding (or contracting) discrete shells on which any basis solution satisfies the wave equation for spaces of all odd dimensions.

In the special case m = 1 the spherical wave operator reduces to

and we have the recurrence

We refer to the ϕ_n as basis solutions, because it’s easy to see that if ϕ_n(r,t) is a solution, then so is kϕ_n(jr,jt) for any constants k and j. For example, each of the following expressions are solutions for n = 5:

and so on.  Any linear combination of these solutions is also a solution, so by means analogous to Fourier series we can construct arbitrary functions of the form

and similarly for G_s(r–t) and G_c(r–t). The analogous functions can be constructed from the basis solutions for any odd n, so the spherical wave equation in n space dimensions is satisfied by

for arbitrary functions F and G. Notice that the greater of the degree of A_n and the degree of rB_n is (n–3)/2, so the lowest inverse power of r is (n–2) – (n–3)/2 = (n–1)/2. This is consistent with the fact that the energy of a wave is proportional to the square of the amplitude, so the energy per unit “area” of the spherical wave drops in inverse proportion to r^n–1, which is the dimension of the surface of a sphere in n-dimensional space. It’s interesting that, for odd space dimensions greater than 3, the amplitude contains formal terms that drop in inverse proportion to higher powers of r as well. This is in a sense misleading, because the amplitude (and hence the energy per unit area) is continuously changing as the wave propagates to greater values of r, and at the same time the value of the wave function is changing with phase. The wave function is not actually periodic, so the correspondence between energy and “amplitude” contains an ambiguity, which manifests itself in the higher-order terms in higher dimensions.

See also the note on Waves in Ascending and Descending Dimensions.

Return to MathPages Main Menu