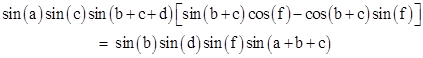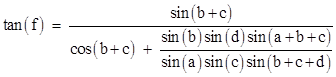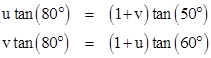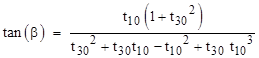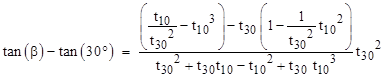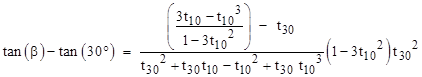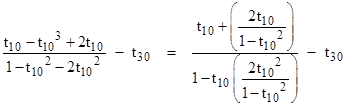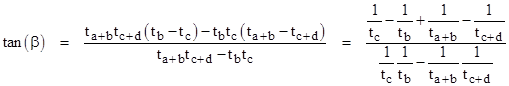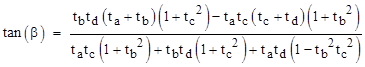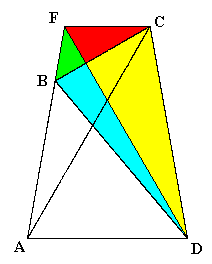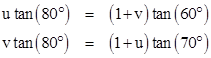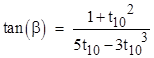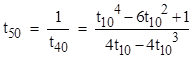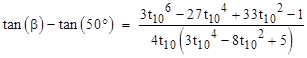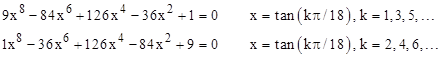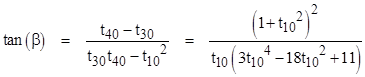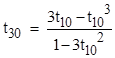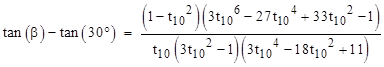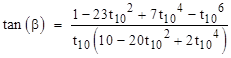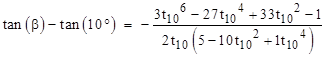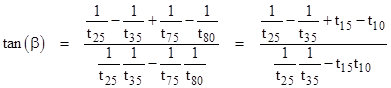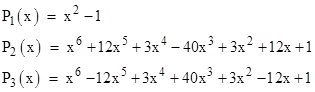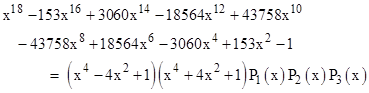Angular Angst

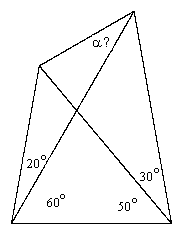
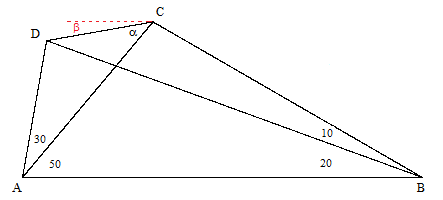
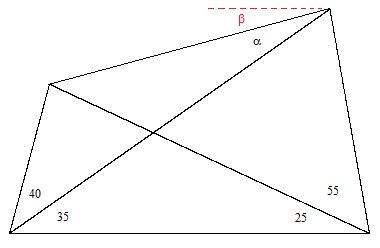
What is the angle denoted by α in the figure below?

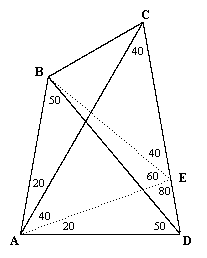
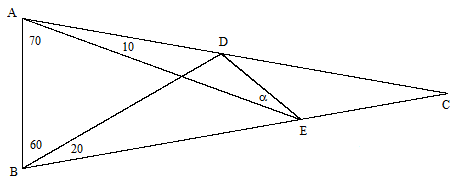
It isn't too difficult to determine with simple trigonometry that α is very nearly equal to 30 degrees, but to rigorously prove that it is exactly 30 degrees is not as trivial as one might think. The problem is usually attributed to Edward M. Langley, who posed it as a puzzle in the Mathematical Gazette in 1922 (although the problem has been found in a Cambridge scholarship test that was printed in 1916), and has become known as the problem of "adventitious angles", because only for certain special combinations of angles is it possible for all the angles in the figure to be rational multiples of π. In the particular case illustrated above there are several clever geometrical proofs, including the following proof devised by Mercer in 1923:  Label the vertices of the quadrilateral A,B,C,D, and construct an additional line AE from the lower left vertex making an angle of 20 degrees with the horizontal, as shown below.

The angles ABD and ADB are both 50 degrees, so |AB| = |AD|. Also, since ADE is 80 degrees and EAD is 20 degrees, it follows that AED is 80 degrees and therefore |AD| = |AE|, and hence |AB| = |AE|. Now, since BAE is isosceles and the angle at A is 60 degrees, we know that ABE is an equilateral triangle, which implies that |AE| = |BE|. In addition, since the angles EAC and ECA are both 40 degrees, we know that |AE| = |CE|, and therefore |BE| = |CE|, so the triangle BEC is isosceles. We also know the angle BEC equals 40 degrees (because BEA equals 60 degrees and AED equals 80 degrees), so it follows that the base angles of BEC are both equal to 70 degrees, and hence the angle BCA equals 30 degrees, which was to be proven.

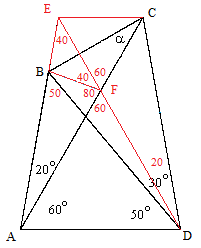
Another solution proceeds by drawing the line CE parallel to AD and intersecting the extension of line AB at point E, as shown below.

We then let F denote the point of intersection of DE and AC. By symmetry it’s clear that ADF and ECF are equilateral triangles, and angle EDC is 20°. We also note that BDA is isosceles. From this it follows that the segments AB, AD, and AF are all of equal length, so BAF is isosceles with an apex angle of 20°, which implies that the base angle AFB is 80°. Since EFC is 60°, it follows that BFE is 40°, and hence EBF is isosceles, so the segment BC bisects the angle ECF. Therefore, angle BCF is 30°, which was to be proven.

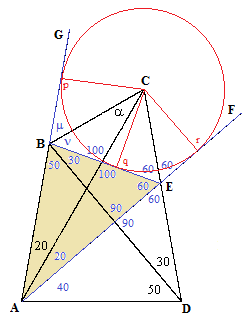
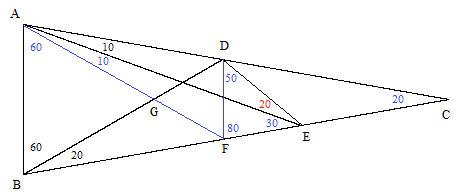
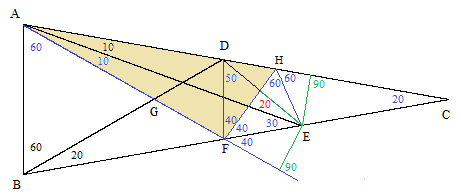
A third solution can be deduced from drawing a line AF through A at 20 degrees from the line AC, and another line EB, and extending the line AB through the point G, as shown in the figure below.

If a circle is inscribed so that it is tangent to the three lines GB, BE, and EF, the perpendiculars from that center to those three lines will have equal lengths, so the center lies on the bisectors of the angles GAF, BEF, and GBE. (In other words, the angular bisectors of any two exterior angles and the opposite interior angle of a triangle pass through a single point.) Now, by construction and simple angular relations, point C in our figure is the unique point that lies on the bisectors of GAF and BEF, so it must be the center of the inscribed circle, and hence it also lies along the bisector of GBE. Consequently we have μ = ν, and since 50+30+μ+ν = 180, it follows that μ = ν = 50°, and therefore α = 30°, which was to be proven.

Several other geometrical proofs have been found. Of course, we can also simply solve for the desired angle by “brute force” using trigonometry. This may lack some of the elegance of the geometrical proofs, but it has the advantage of generality. Consider an arbitrary quadrilateral and its diagonals, as shown below.

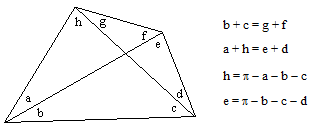
The law of sines implies that the eight angles around the perimeter satisfy the relation

Given the values of four consecutive interior angles around the perimeter, such as a, b, c, and d, the quadrilateral is completely determined, so we can solve for the remaining angles. The values of h and e are immediate, as is the sum g+f, but to determine the individual values of g and f requires some trigonometry. Since sin(π−x) = sin(x), we can substitute for e and h in the preceding expression to give

We can also replace g with b + c − f and expand the resulting sine to give

Dividing through by cos(f) and solving for tan(f), we have

With this (or any equivalent) formula we can numerically evaluate the angles of any given “quadrangle”. However, although this may suffice for practical purposes (since with computers we can calculate the angles to any desired precision), this formula with its mixture of sines, cosines, and tangents, doesn’t directly provide a general method of proving that the computed angles are exact rational multiples of π.

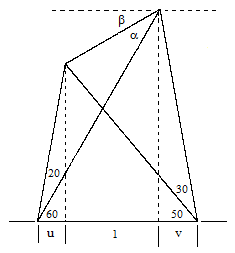
For a slightly different trigonometric approach, leading to an expression involving only the tangents of the elementary angles, note that the diagonal going from lower left to upper right makes an angle of 60° with the horizontal, so α + β also equals 60°. Therefore, in order to show that α = 30° it suffices to show that β = 30°, i.e., that the upper side of the quadrilateral makes an angle of 30° with the horizontal. To show this, we begin by assigning variables to the important lengths as shown below. (Since the scale is unimportant, we have normalized so that the horizontal distance between the two altitudes is unity.)

We have tan(β) = (v – u) tan(80°) where u and v are related by

For convenience, we will hereafter denote tan(k°) by t_k. From the above relations we get

Therefore we have

where we have made use of the facts that t₆₀ = 1/t₃₀, t₅₀ = 1/t₄₀, and t₈₀ = 1/t₁₀. Now, substituting for t₄₀ with the trigonometric identity t₄₀ = (t₃₀ + t₁₀)/(1 – t₃₀ t₁₀), we get

Subtracting t₃₀ from both sides, we have

Making use of the fact that 1/t₃₀² = 3, this can be written as

The numerator of the fraction can also be written as

The quantities in parentheses are simply t₂₀, so the numerator of the fraction in the previous expression is

where the first term on the left side is simply the tangent of 10° + 20°. Therefore, tan(β) = tan(30°), so we have β = 30° and hence α = 30°, which was to be proven. (Incidentally, this leads to several interesting identities, such as t₁₀ = t₂₀ t₃₀ t₄₀.) We will see below how this kind of proof can be generalized to arbitrary quadrangles, with angles that are arbitrary rational multiples of π.

Incidentally, by applying the above “tangent” analysis to the general quadrangle, we find that the angle β which the upper edge (from the vertex of angle f) makes with the horizontal is

where t_a denotes tan(a) and so on. Expanding the tangents of the summed angles, this can be written in terms of the tangents of the individual angles as

Furthermore, knowing that f + β = b, we can use the tangent addition formula to give the explicit expression

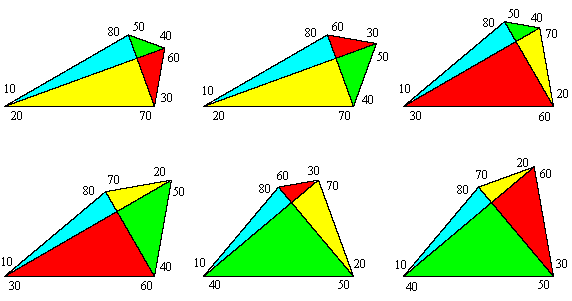
(The form of the numerator hints at a connection with Ceva’s Theorem.) As with the previously derived trigonometric formula, we can apply this formula numerically to discover that the original “Langley” construction is far from unique. One of the interesting categories of such solutions consists of quadrilaterals with perpendicular diagonals. If we focus on those whose angles are unequal multiples of 10 degrees (i.e., p/18), any such quadrilateral must be comprised of a 10:80, a 20:70, a 30:60, and a 40:50 triangle. It isn't self-evident that four triangles with these shapes can be combined into a single quadrilateral, but in fact they can, in the six distinct ways shown below.

Langley's original example of adventitious angles involves the upper left case, as illustrated in the figure below:

This shows Langley's original quadrilateral ABCD, but the line AB has been extended to the point F, and the horizontal line FC has been drawn. The quadrilateral DBFC is a "10:20:30:40 " quadrilateral with perpendicular diagonals BC and DF.

Another example that is often mentioned along with Langley’s original puzzle is the isosceles triangle shown in the figure below.

As with the original puzzle, several clever geometrical proofs for this example are know. The most common proof begins by drawing a line from A to the point on BC that is directly below D. By symmetry this line must make an angle of 60 degrees from AB, as shown in the figure below, where we have also indicated several of the angles that can be immediately deduced.

By construction, triangles ABG and DFG are equilateral, and triangle AFC is isosceles. It follows that AF = CF. Also, since the line bisecting angle CAF strikes CF at E, and the line (not drawn) bisecting ACF strikes AF at G, we have AG = CE, and therefore GF = FE. Now, since DF = GF, we see that DFE is isosceles. Combined with the fact that the angle DFE is 80°, it follows that angle DEF is 50°. We know that AEB is 30°, so AED is 20°, completing the proof.

By the way, if we draw a line bisecting the angle DFE and striking DC at the point H, the point E is an “excenter” of the triangle AFH.  In other words, E lies on the bisectors of two external angles and the opposite internal angle of AFH, as shown below.

From this we can infer that the angles at H are 60°. This is similar to the second proof of Langley’s original problem described previously, except in this case the relevant angle is of the radius of the circle to the tangent point on the line FH. However, to prove that the line DE is perpendicular to FH, we still need to show that DFE is isosceles, and once we know this, we can already determine the desired angle, without needing to invoke the excenter property of point E.

The geometrical proofs for this problem seem to be quite distinct from the proofs of the original Langley problem. It would be more satisfying to have a general method that applies to all such problems, and doesn’t rely on special features of any particular example. To determine such a method, we begin by applying the same trigonometric approach that we applied to the original problem, which in this case amounts to finding the angle β between vertical and the line DE. We know that AE makes an angle of 70° with vertical, so we expect to find β = 50°, which will imply that the desired angle AED is 20°. Proceeding just as in the previous case, we have tan(β) = (v – u) tan(80°) where u and v are related by

As before, we will denote tan(k°) by t_k. From the above relations we get

Therefore we have

where we have made use of the facts that t₆₀ = 1/t₃₀, t₇₀ = 1/t₂₀, and t₈₀ = 1/t₁₀. Now, making the substitutions t₃₀ = (t₂₀ + t₁₀)/(1 – t₂₀ t₁₀) and t₂₀ = 2t₁₀/(1−t₁₀²), we get

By use of the tangent addition formula, we have the trigonometric identity

Subtracting this from tan(β) and simplifying, we have

At this point it’s convenient to recall from the article on Linear Fractional Transformations that the quantities tan(kπ/(2n))² are the roots of the polynomial whose coefficients are alternating terms (with alternating signs) of the nth row of binomial coefficients. For example, we have the trigonometric identities

Now, the first of these has the factorization

The second factor with x = t₁₀ is identical to the numerator of tan(β) – tan(50°), which implies tan(β) = tan(50°), so we have β = 50° and hence α = 20°, which was to be proven.

This may seem significantly different from our trigonometric proof of Langley’s original problem, but only because for that problem we exploited the fact that the resulting angle happened to be 30°. We could just as well have applied the more general method, working entirely in terms of t₁₀, noting that we have (for Langley’s original problem)

and the trigonometric identity

Taking the difference between these two expressions gives

Again the numerator vanishes because it contains the same factor as discussed above. This is the minimal polynomial with integer coefficients having the value t₁₀ as a root, so any expression in terms of t₁₀ that vanishes must contain this factor.

To illustrate the generality of this method, consider the quadrangle shown in the figure below.

Using the general formula given previously, we can write the tangent of the angle β that the edge CD makes with the horizontal (i.e. parallel to AB) as

Then we can prove that β = 10° by noting that the difference

has the very same polynomial in the numerator as the previous examples, which vanishes identically, proving that β = 10° and therefore α = 40°.

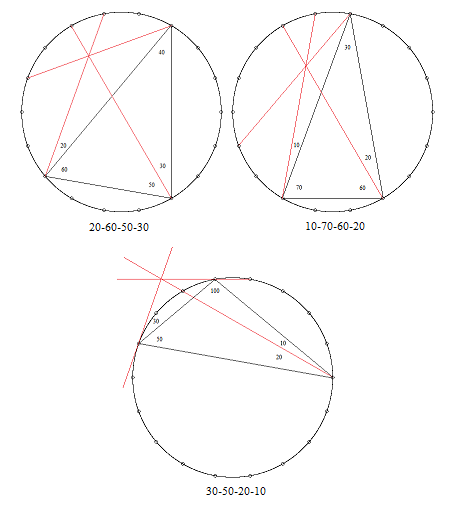
Advantitious quadrangles can be characterized in terms of chords of a regular n-gon. Each such quadrangle corresponds to three chords that intersect at a single point. For example, the quadrangles discussed above are shown with their associated chords of an 18-gon in the figures below.

Note that a “chord” through a single vertex is defined as the tangent to the circle (i.e., perpendicular to the radial line from the center of the n-gon) at that vertex. The 30-50-20-10 quadrangle provides an example of this. It also shows that the triple intersection point may lie outside the n-gon.

All the above was based on quadrangles whose angles were multiples of 10°, i.e., integer multiples of π/18, but we can obviously perform the analogous analysis for any quadrangle whose angles are any rational multiples of π. For example, consider the quadrangle whose angles are integer multiples of 5° (i.e., π/36) in the figure below.

Using the formula given above, we know tan(β) is given by

Using the tangent addition formula we can express each of the tangents in this expression as rational functions of t₅, and then, since we expect β = 15°, we evaluate the difference

where

As explained previously, t₅ is a root of the polynomial whose coefficients are alternate terms (with alternating signs) from the 18^th row of binomial coefficients. That polynomial factors as

This shows that P₃(t₅) = 0, which proves that tan(β) – tan(15°) is zero, and so β = 15°, which implies α = 20°. Since P₃ is the minimal polynomial (with integer coefficients) having the root t₅, it will appear as a factor in every proof of this type for quadrangles whose angles are integer multiples of 5°.

The note on Adventitious Solutions provides some further examples, and includes a discussion of how the other roots of the characteristic polynomials lead to families of related adventitious quadrangles.

Return to MathPages Main Menu