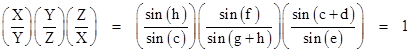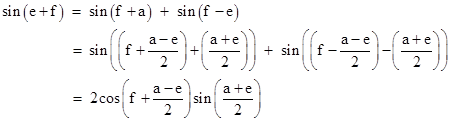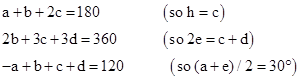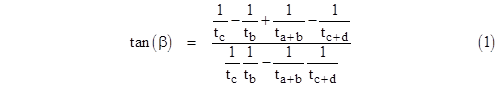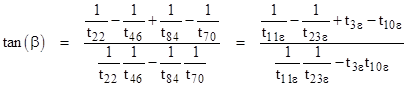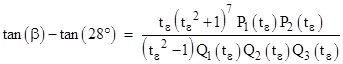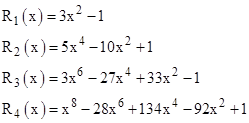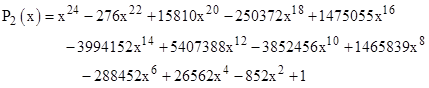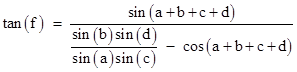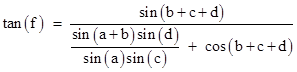Adventitious Solutions

The solution of Langley’s problem of adventitious angles can be given (in several ways) as a simple geometric argument, but one also sometimes sees “trigonometric solutions”. There are three main types of such solutions. The first is to simply give an explicit expression for the desired angle in terms of trigonometric functions, typically by computing the tangent of the desired angle, and then taking the inverse tangent. However, this is really a numerical solution, in the sense that it can be carried out to arbitrary precision, but it can never provide a proof of the exact value of the desired angle (a rational multiple of π). A second type was described in the note Angular Angst, by expressing the desired angle in terms of the tangent of the fundamental angle, and then showing that the difference between this and the tangent of some integer multiple of that fundamental angle is divisible by the minimal polynomial whose roots include the tangent of that angle. This is a genuine algebraic solution, about which we will have more to say below.

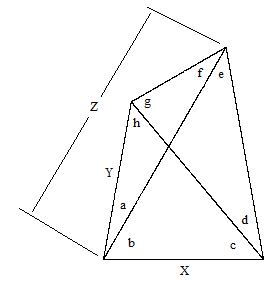
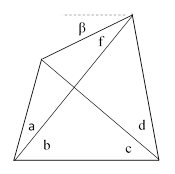
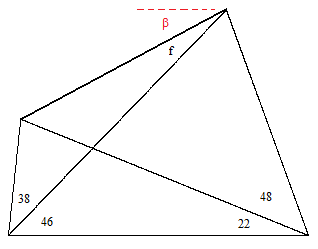
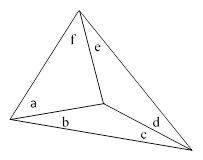
First we will comment on a third type of “trigonometric solution” that one sometimes sees for a certain specific problem, making use of the special conditions of that problem. This type of solution does not provide a general method, so it resembles the ingenious geometrical proofs that have been devised for individual special cases. Nevertheless it’s interesting to examine this approach in detail. Consider the general quadrangle shown below.

In the usual problem the angles a,b,c,d are given, from which we can immediately determine e and h, as well as the sum g + f. The task is to determine f. By the law of sines we have

Therefore we have

Now, it so happens that, in Langley’s original problem, we have h = c, so we can cancel those sines from both sides. Also, in terms of angular degrees, we know that g + h = 180 – a – f, and from the trigonometric identity sin(x) = sin(180 – x) it follows that sin(g+h) = sin(a+f). Thus the above expression can be written as

Another fortuitous feature of Langley’s original problem is that c+d = 2e, so we can make use of the trigonometric identity sin(2x) = 2cos(x)sin(x) to express sin(c+d) as 2cos(e)sin(e), and hence the above relation reduces to

Now we can use the trigonometric identity 2cos(x)sin(y) = sin(x+y) + sin(x–y) to expand the left hand side, giving the relation

Re-arranging terms, this can be written as

At this point we note that, in Langley’s original problem, (a+e)/2 = 30°, so the sine on the right hand side equals 1/2, and the equation reduces to

Since cos(x) = sin(90 – x), this can be written as

Hence we have e + f = 90° – f – (a-e)/2, which implies f = 45° – (a+e)/4. Furthermore, as noted above, the solution works only on the condition that (a+e)/2 = 30°, and so f = 30°. This is undeniably a valid solution, but it relies on the following three separate fortuitous facts:

These conditions imply b = 3a, c = 90° – 2a, and d = 30°, so there is really only a single degree of freedom in the values of a, b, and c, and if these conditions are satisfied the solution is f = 30°, regardless of the value of a. Thus for any quadrangle with the angles

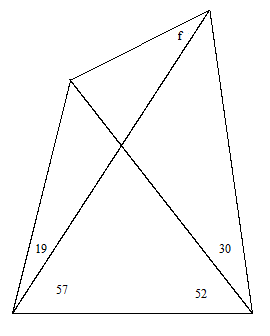
the same “trigonometric solution” applies, and it identically yields the answer f = 30°. Therefore, this solution method applies only to quadrangles for which the solution is 30°. In this sense it is a purely ad hoc solution method, similar to the geometrical solutions. An example of the class of quadrangles for which this solution is applicable, with a = 19°, is shown below.

Since these angles satisfy the conditions of the “trigonometric solution”, it yields the answer f = 30°. This is the only answer that this solution method can possibly give, because the method is applicable only under conditions for which the answer is 30°. This “method” completely lacks the generality of a genuine algebraic solution, such as the one described in the note on adventitious angles.

Returning to the genuine algebraic solution method described in the previous note, recall that we are considering the general configuration shown below for any given set of base angles a, b, c, and d.

All the angles are stipulated to be rational multiples of π, so each of the angles is an integer multiple of some elementary angle. For example, in Langley’s original puzzle all the angles are integer multiples of π/18 (i.e., 10°). Therefore, using the simple addition formula for tangents, we can express the tangent of each base angle as a ratio of polynomials in the parameter t = tan(π/18) with integer coefficients. With these expressions, and letting t_a denote tan(a), etc., we can then use the formula from the previous note

to write the tangent of the angle β (defined for convenience as the angle between the base edge and the opposite edge) as a ratio of polynomials in t with integer coefficients. (We can use the identity tan(x) = 1/tan(π − x) to ensure that we need tangents of angles no greater than π/2.) From this we can subtract the tangent of the putative value of β constructed by the tangent addition formula (since β is also an integer multiple of the elementary angle). The numerator polynomial of the resulting difference vanishes if and only if β does indeed have the putative value. The desired angle f is then given by f = b – β. We determine that this polynomial vanishes by noting that it contains a factor from the polynomial with coefficients from the appropriate row of Pascal’s triangle, whose roots are identically the tangents of the odd integer multiples of the elementary angle.

Letting ε denote the elementary angle, in Langley’s original puzzle we have ε = π/18, and the given base angles are a = 2ε, b = 6ε, c = 5ε, and d = 3ε. From this we determine that b = 3ε and therefore f = 3ε, because tan(ε) is a root of the polynomial

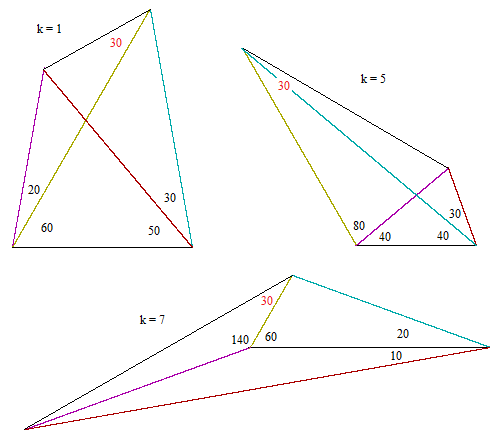
It’s worth noting that this same derivation applies to any elementary angle that is a root of this equation. By construction, the roots are ±tan(π/18), ±tan(5π/18), and ±tan(7π/18). In general, the minimal polynomial with the root tan(π/N) also has the roots ±tan(kπ/N) for every k co-prime to N. Thus we have ϕ(N)/2 essentially distinct roots, where ϕ is Euler’s totient function. (For example, ϕ(18) = 6.) As a result, we find that Langley’s original puzzle is actually equivalent to the three configurations shown below.

In each case the angles are k times the angles from Langley’s original quadrangle. For example, the left hand edge in the k = 1 configuration makes an angle of 80° with the base edge, so with k = 5 it makes an angle of 5(80°) = 400°, which equals 40° modulo 360°. The desired angle f in this case is actually 5(30°) = 150°, but this gives the interior angle of 180° − 150° = 30°. We note that the k = 7 configuration has one of the vertices inside the triangle formed by the other three, so the outline is a triangle, but it still represents a valid quadrangle.

For another example, consider the quadrangle shown below.

In this case the greatest common divisor of the base angles is only 2°, i.e., π/90, so we take this as our elementary angle ε. Equation (1) then gives

Numerically we can easily determine that β is 28°, and we can use the tangent addition formula to express t_14ε, t_3ε, t_10ε, t_11ε, and t_23ε in terms of t_ε to give

where P₁ is an “even” polynomial of degree 16 and P₂ is an “even” polynomial of degree 24. (The degrees of the polynomials in the denominator are 6, 6, and 40.) Now, the polynomial whose coefficients are alternate values (with alternating signs) from the 45^th row of Pascal’s triangle is

where

The remaining factor is

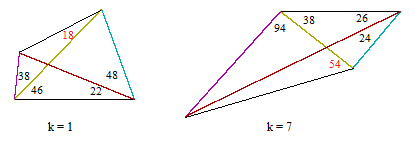
which is identical to the polynomial P₂ in the numerator of tan(β) – tan(14ε). The roots of P₂ are kπ/90 for each k co-prime to 90. Therefore, although the original derivation was based on ε = π/90, the very same derivation applies if we set ε = kπ/90 where k is any integer co-prime to 90. The totient of 90 is ϕ(90) = 24. Since the polynomial is “even” (i.e., only even powers), each root appears with both positive and negative signs, so there are only 12 distinct roots up to sign, corresponding to k = 1, 7, 11, 13, 17, 19, 23, 29, 31, 37, 43, and 47. The configurations given by k =1 and k = 7 are shown below.

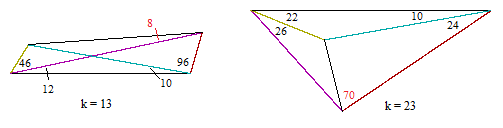
The configurations for k = 11, 17, and 19 involve very small angles that are difficult to show graphically. The configurations given by k = 13 and k = 23 are shown below.

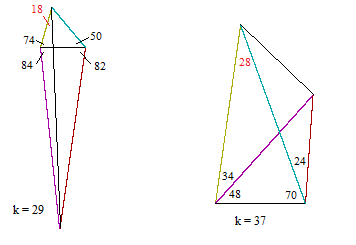
The configurations for k = 31, 43, and 47 are difficult to show graphically. The configurations given by k = 29 and k = 37 are shown below.

All these configurations of “rational quadrangles” are algebraically equivalent.

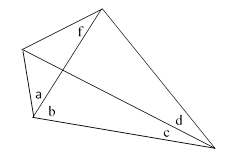
As noted above, rational quadrangles may have one of their vertices inside the triangle formed by the other three. For such configurations the connection with Ceva’s Theorem is particularly apparent. Consider the quadrangle shown below.

The angular form of Ceva’s Theorem asserts that

Also we know that e = 180° – (a+b+c+d+f), and that sin (180° − x) = sin(x), so we have

Using the sine addition rule sin(x+y) = sin(x)cos(y) + sin(y)cos(x), we can isolate the angle f on the left side and then divide through by cos(f) and solve for tan(f), to give the result

This applies to quadrangles with an interior vertex. If the interior vertex is moved across the a-f edge, the angle a becomes –a and the angle b becomes a+b, and the angle f is also negated. With these re-assignments, the quadrangle takes the form

and the formula for quadrangles such as this (i.e., with no interior vertices) is

This is slightly more economical expression than the one developed in Angular Angst based on a straight-forward application of the law of sines.

Return to MathPages Main Menu