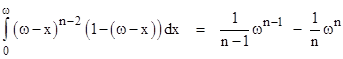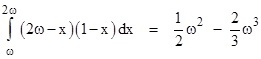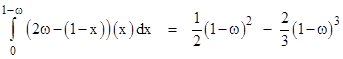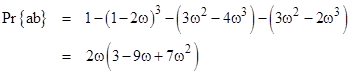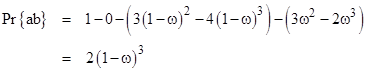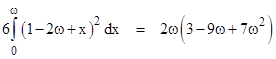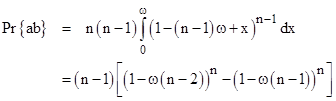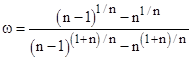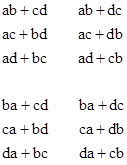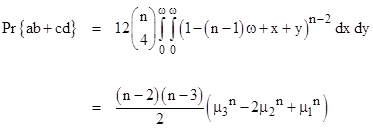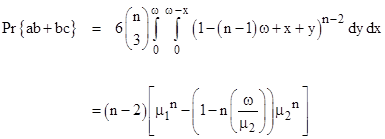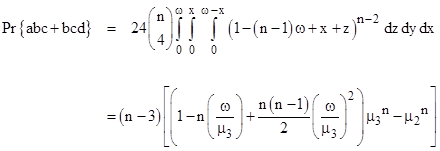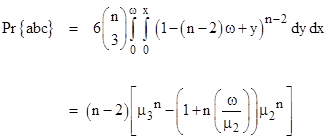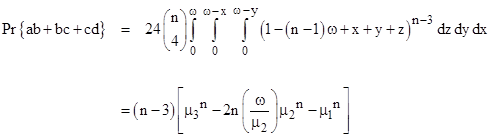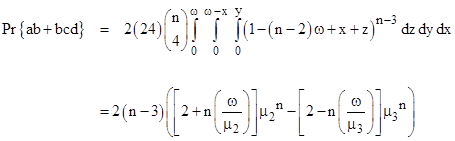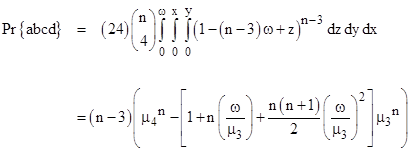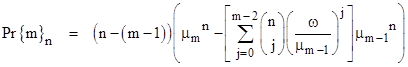Probability of Intersecting Intervals

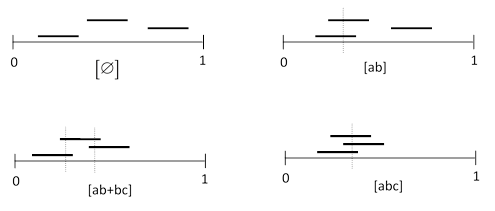
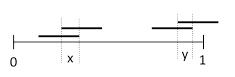
Suppose the left-most points of n segments of length ω are placed on the unit interval. In general there are many different patterns of intersection (meeting combinations) that can occur. Examples of the four types of outcomes for n = 3 are shown below.

The expressions inside the square brackets signify the structure of the set of intersections. Note that we take the n segments to be inter-changeable. What is the probability of each of these four types of outcomes?

For the case of no intersections the distance between every two consecutive starting points must be greater than ω, so the n starting points are effectively constrained to (and uniformly distributed on) a region of length 1 – (n – 1)ω. Each of the n starting points can be placed anywhere in this span, so the total volume of the region equals the nth power of this length, and of course the total overall volume for all possible arrangements is the nth power of the unit interval, so the probability of no intersections is

Of course, strictly speaking, this equation is valid only for segments with ω less than or equal to 1/(n–1), because for larger values of ω the quantity in square brackets is negative. The probability of no intersections for ω greater than 1/(n–1) is zero.

At the opposite extreme, i.e., the case in which all n segments overlap with each other, the first and last starting points must be separated by a distance ω – x for some x between 0 and ω, and the remaining n – 2 starting points can be anywhere in the intervening span, and the first starting point can be placed anywhere in a span of length 1 – (ω – x). Thus the volume of the region is given by the integral

This accounts for the n–2 “interior” points being placed in any order, but we must choose 2 of the n points for the first and last starting points, which implies that we must multiply the above integral by n!/(n–2)! = n(n–1) to give the total volume of the desired region. Consequently we have

This formula applies for all values of ω from 0 to 1.

To determine the probability of the meeting combination “ab+bc” for n = 3, we note that the the distance between the first and last starting points must be no less than d and no greater than 2ω. Letting x denote the distance between the first and last starting points, the intermediate starting point must lie within a range 2ω – x, and the first starting point ranges from 0 to 1 – x, so the volume of the region is

assuming w is less than or equal to 1/2 so that the factor 1 – x is non-negative when x equals 2ω. Again we must choose 2 of the 3 starting points to be the first and last, so we must multiply the integral by 3!/1! = 6 to give the probability

For ω greater than or equal to 1/2 the intermediate starting point falls within a range of size 2ω – 1 + x as x ranges from 0 to 1 – ω, and the entire configuration can slide over a range of x, so the volume of the region is

Again we multiply by 6 to give the probability

The probability of the remaining combination for n = 3 can then be determined by the requirement for the sum of the probabilities for all four combinations to equal unity. Thus we have

for ω less than or equal to 1/2, and

for ω greater than or equal to 1/2. The probability of the outcome “ab” (for ω less than or equal to 1/2) can also be determined directly by noting that two of the intervals must overlap each other by an amount x and the third does not overlap with any other interval, so for any given x from 0 to ω we effectively have just two segments, whose starting points are constrained to lie within a region of length 1 – 2ω + x (regardless of whether the overlapping pair occurs first or second). The square of this length gives the measure of the region. There are six ways of choosing the first and second overlapping segments, so the volume of the region is

which agrees with the previous result. The same reasoning gives the probability of exactly two of n segments overlapping for arbitrary n (for ω less than or equal to 1/(n–1)).  In general we have

When ω equals 1/(n–1), the upper limit of the range of applicability for this expression, the probability is simply (n–1)^(1–n). Differentiating this with respect to w and setting the result to zero, we find that (in the applicable range) this probability is maximized at the value of ω given by

Inserting this back into the expression for Pr{ab}, we find that the maximum probability of exactly two of n segments (of length less than 1/(n–1)) overlapping approaches 1/e in the limit as n goes to infinity.

Formulas for the probabilities of other meeting combinations can be determined in the same way. For example, to find the probability of exactly two pairs of intersecting intervals, i.e., the meeting combination ab + cd, note that the four segments a,b,c,d comprise two spans with overlaps of lengths x and y, as shown below.

For any given values of x and y from 0 to ω, the starting points of these two compound segments are constrained to lie in a span of length 1 – (3ω – x – y). Also, there are twelve distinct permutations of the four segments, namely,

Notice that the order of the factors in any product matters, but the order of summands does not. For this reason, including additional isolated segments does not affect the number of distinct permutations. Thus, the inclusion of any number of such segments merely increments the number of “ω”s deducted from the free span, and increments the exponent. In general, then, the probability of {ab+cd} is

where

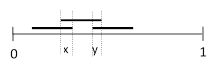
For another example, consider the combination {ab+bc}, in which one segment overlaps with each of two other segments, but those two segments don’t overlap with each other, as shown below.

where x + y is less than or equal to ω. For any three segments a,b,c there are six distinct ways in which this structure can be achieved, namely, abc, cba, bac, cab, acb, and bca, and the starting point of this single compound span along with the starting points of any number of isolated spans are constrained to lie on a region of length [1 – (n–1)ω + x + y]. Therefore, the probability of this meeting combination is

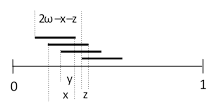
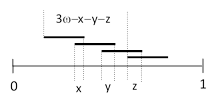
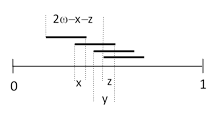
For another example, consider the meeting combination abc+bcd, letting x denote the overlap between a and b, and y the overlap between a and c, and z the overlap between b and d, as shown below.

The distance between the first and last starting points is 2ω–x–z, so we need only integrate the complement of this quantity as x ranges from 0 to w, y ranges from 0 to x, and z ranges from 0 to ω–x. There are 24 possible permutations of these four segments, and the inclusion of any additional isolated segments would simply require a factor of “n choose 4” and incrementing the exponent and the coefficient of ω in the integrand. Therefore the probability is

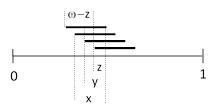
Next we consider the case of exactly three of n segments intersecting with each other, i.e., the meeting combination {abc}. If n = 3 this is the case designated as “all” previously. In general the three overlapping segments are as shown below.

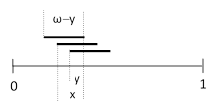
Here x is the overlap between a and b, and y is the overlap between a and c. The length of the span from the first to the last starting point is ω – y, so we need to integrate the complement of this as x ranges from 0 to ω and y ranges from 0 to x. There are six distinct permutations of a,b,c, so the probability that the intersections of n segments will consist of three overlapping segments is

The next case to consider is the meeting combination {ab+bc+cd}, as illustrated in the figure below.

By the same reasoning as for the previous cases, we see that the probability that the intersections between n segments consist of just this combination is

Next we consider the case {ab+bcd}, which can also occur as {abc+cd}, so there is an extra factor of 2 in the usual expression. (When summands share common factors the order of the summands becomes significant, because the terms are linked.) The typical case is shown in the figure below.

Applying the same reasoning as before, we get the result

Lastly we consider the case {abcd}, which signifies that the intersections of the n segments consist of the overlap of four segments. If n = 4 this is the same as the case when all segments overlap (as derived previously), but for n greater than four it is different. A typical example of this case is illustrated below.

For this case we integrate the complement of ω – z as x ranges from 0 to w, y ranges from 0 to x, and z ranges from 0 to y. This gives the result

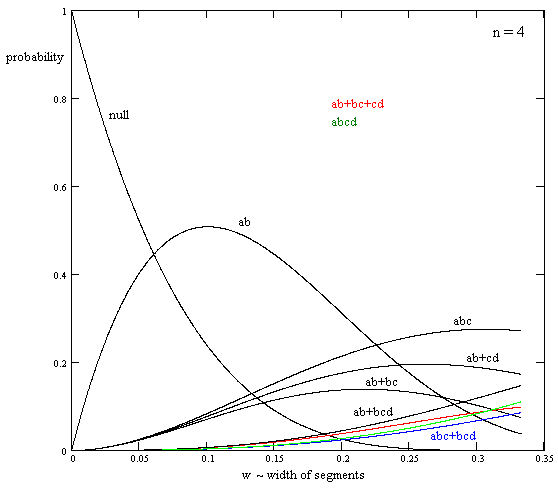
The only other meeting combination involving four our fewer segments is ab+ac+ad, but this cannot occur with all segments having the same length, so the nine cases described above represent all the possible cases for n segments of length ω < 1/(n–1) in which no more than four segments are involved in any intersections. Therefore, with n = 4, these nine functions of ω, as shown in the plot below, sum to unity.

See Meeting Probabilities for a discussion of cases when the individual segments have different lengths.

Incidentally, by examining the cases {ab}, {abc}, and {abcd}, it’s easy to see that the general expression for the probability that exactly m of n segments will intersect (and none of the other n – m segments will intersect with each other) is

Of course, if we want the probability that the intersections will include at least one m-way intersection, without excluding the cases when it includes additional intersections, then we need to account for other terms. For example, the probability of at least one 3-way intersection for n = 4 segments is the sum

and for higher values of n it would be necessary to include still more terms to account for all the meeting combinations that include at least one 3-way intersection.

Return to MathPages Main Menu