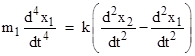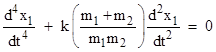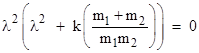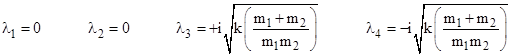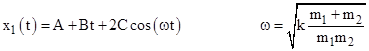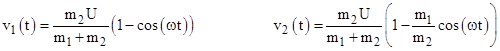Resonance and Motion

The existence of secular motion is made possible by a repeated root of a certain characteristic equation, and the law of inertia can be attributed to the fact that there is only one repeated root. For example, in terms of an inertial coordinate system x,t, the equation of motion of a free particle is simply d²x/dt² = 0, which has the trivial characteristic equation s² = 0 with the two roots λ₁ = λ₂ = 0. The repeated root represents a “resonance”. The general form of the solution with two equal characteristic values (not necessarily zero) is

where c₁ and c₂ are constants. The factor of t in the second term is due to the resonance. Thus the space coordinate is a linear function x(t) = c₁ + c₂t of the time coordinate, and similarly for the y and z coordinates, so the particle moves uniformly in a straight line.

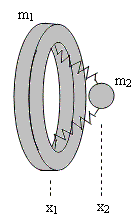
For more complicated motions involving interactions between objects, any closed isolated system will always possess a resonance of degree 2, since the fundamental law of motion involves only the second derivative. Consider, for example, a ball and ring connected by springs as shown below.

For simplicity, assume the spring exerts a restoring force on the ball and ring proportional to the displacement (in the x direction) between them. Then the equations of motion are

Hence we have

Differentiating the original equation for x₁ twice with respect to time gives

and substituting from the preceding equation to eliminate x₂, we get the equation for the position x₁ of the ring:

The characteristic polynomial of this equation is

so the eigenvalues are

For each distinct root λ the general solution contains a term of the form Ae^λt, but the duplicate root implies that the solution contains a term of the form Ate^λt. As noted above, duplicate roots are sometimes called resonances. Thus the general solution for this system is

For real-valued solutions we must have C = D, and hence the solution is of the form

The constant A represents, in a sense, the relativity of spatial position, and the cosine term simply represents a bound oscillation. The overall secular motion of the system is represented by the “resonance” term Bt, which due to the presence of the repeated roots λ₁ = λ₂ = 0. On the other hand, if there were any additional repeated zero roots, there would be terms proportional to t², t³, and so on, implying that for some initial conditions the free motion would have secular acceleration. The presence of exactly one repeated root represents the relativity of the state of uniform motion, meaning that the average spatial coordinate over a sufficiently long time is a linear function of the time coordinate. Thus the principle of inertia is a consequence of the single resonance. (This represents a true resonance, in contrast with the attempts of some authors to describe the relativistic precession of Mercury’s orbit as a resonance effect.)

The cosine differs from the sine only by a phase angle, so the general solution can just as well be written as

for suitable values of the constants X, V, and A₁. In this form the constant X represents the initial position at time t = 0. The derivative of the spatial position is

Therefore, if the ring is stationary at t = 0, we must have V = −ωA₁. The constant V represents the overall long-term velocity of the system, and A₁ is the amplitude of the oscillation of the ring relative to the mean inertial path.

The equation of motion of the ball is the same as of the ring, and the general solution has the same form. Also, the long-term position of the ball is always within a fixed distance from the ring, so the coefficient to t must be V. Furthermore, if we stipulate that the initial position of the ball is X at time t = 0, then the general solution has the form

for suitable constant A₂. The derivative is

Thus if we let U denote the initial speed of the ball at time t = 0, we have V+ωA₂ = U. Combining this with the previous relation V = −ωA₁, we get

Conservation of momentum requires

which can be written as

Since this must hold continuously for all t, we have the two separate conditions

The right-hand condition gives (as expected)

and combining the left-hand condition with A₂ – A₁ = U/ω gives

These represent the amplitudes of the oscillations about the mean trajectory of the system, so in terms of coordinates in which the overall system is stationary these constants signify the kinetic agitations of the ring and ball, respectively. The maximum kinetic energies of the two components (relative to this frame) can be represented by half the masses times the squared maximum speeds. The maximum speeds relative to this frame (i.e., after transforming V to zero) are ωA₁ and ωA₂ respectively, so we have the maximum kinetic energies

Thus the ratio of kinetic energies is inversely proportional to the ratio of the masses.

Using the above results, we find that the overall time-dependent speeds of the ring and ball relative to the original frame of reference are

These equations shown that the system periodically returns to its initial velocity configuration, i.e., v₁ = 0 and v₂ = U, although the spatial position advances progressively between these conditions. We can imagine a ball initially moving freely through space with speed U, and at some point encountering and being ensnared by the springs of the stationary ring. The combined configuration could then proceed through several oscillatory cycles and then we could contrive to release the ball at some instant when x₁ = x₂ and v₂ = U. The ball would go on at its original speed U and the ring would be left stationary again, but its position would have been changed. Note that the center of mass of the ring and ball throughout this scenario continues to move uniformly in a straight line. The displacement of the ring corresponds to a delay in the progress of the ball. We might say that the interaction has resulted in a spatial shift of the ring and a compensatory temporal shift of the ball.

The above discussion focused on a simple two-component system, but it shows that, in general, the components of any isolated system must be coupled by equations involving the second derivatives, and not the first or zeroth derivatives, of their positions. This is required so that the characteristic polynomial of the equation of motion has a factor of λ², meaning it has precisely two roots equal to zero, leading to an equation for the center of mass of the form A + Bt, consistent with the principle of inertia.

Return to MathPages Main Menu