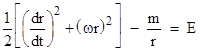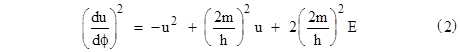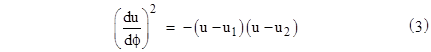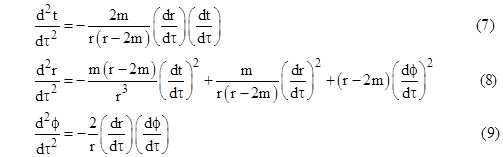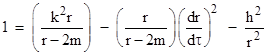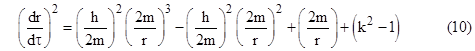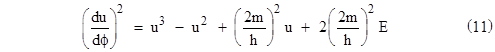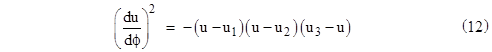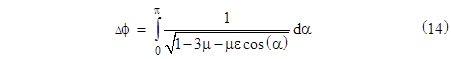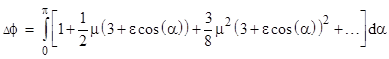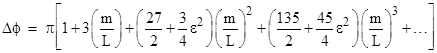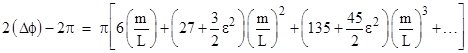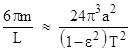6.2  Anomalous Precessions

In these last months I had great success in my work. Generally covariant gravitation equations. Perihelion motions explained quantitatively… you will be astonished.

                                                                                             Einstein to Besso, 17 Nov 1915

The Earth's equatorial plane maintains a nearly constant absolute orientation in space throughout the year due to the gyroscopic effect of spinning about its axis. Similarly the plane of the Earth's orbit around the Sun remains essentially constant. These two planes are tilted by 23.5 degrees with respect to each other, so they intersect along a single line whose direction remains constant, assuming the planes themselves maintain fixed attitudes. At the Spring and Autumn equinoxes the Sun is located precisely on this fixed line in opposite directions from the Earth. Since this line is a highly stable directional reference, it has been used by astronomers since ancient times to specify the locations of celestial objects. (Of course, when we refer to "the location of the Sun" we are speaking somewhat loosely. With the increased precision of observations made possible by the invention of the telescope, it is strictly necessary to account for the Sun's motion about the center of mass of the solar system. It is this center of mass of the Sun and planets, rather than just of the Sun, that is taken as the central inertial reference point for the most precise astronomical measurements and calculations.) By convention, the longitude of celestial objects is referenced from the direction of this line pointing to the Spring equinox, and this is called the "right ascension" of the object. In addition, the "declination" specifies the latitude, i.e., the angular position North or South of the Earth's equatorial plane.

This system of specifying positions is quite stable, but not perfect. Around 150 BC the Greek astronomer Hipparchus carefully compared his own observations of certain stars with observations of the same stars recorded by Timocharis 169 years earlier (and with some even earlier measurements from the Babylonians), and noted a slight but systematic difference in the longitudes. Naturally these were all referenced to the supposedly fixed direction of the line of intersection between the Earth's rotational and orbital planes, but Hipparchus was led to the conclusion that this direction is not perfectly stationary, i.e., that the direction of the Sun at the equinoxes is not constant with respect to the fixed stars, but precesses by about 0.0127 degrees each year. This is a remarkably good estimate, considering the limited quality of the observations that were available to Hipparchus. The accepted modern value for the precession of the equinoxes is 0.01396 degrees per year, which implies that the line of the equinoxes actually rotates completely around 360 degrees over a period of about 26,000 years. Interpreting this as a gradual change in the orientation of the Earth's axis of rotation, the precession of the equinoxes is the third component of what Copernicus called the "threefold movement of the Earth", the first two being a rotation about its axis once per day, and a revolution about the Sun once per year. Awareness of this third motion is arguably a distinguishing feature of human culture, since it can only be discerned on the basis of information spanning multiple generations.

The reason for mentioning this, aside from expressing admiration for human perspicacity, is that when we observe the axis of the elliptical orbit of a planet such as Mercury (for example) over a long period of time, referenced to our equinox line, we must expect to find an apparent precession of about 0.01396 degrees per year, which equals 5025 arc seconds per century, assuming Mercury's orbital axis is actually stationary. However, astronomers have actually observed a precession rate of 5600 arc seconds per century for the axis of Mercury's orbit, so evidently the axis is not truly stationary. This might seem like a problem for Newtonian gravity, until we remember that Newton predicted stable elliptical orbits only for the idealized two-body case. When analyzing the actual orbit of Mercury we must also take into account the gravitational pull of the other planets, especially Venus and Earth (because of their proximity) and Jupiter (because of its size). It isn't simple to work out these effects, and unfortunately there is no simple analytical solution to the n-body problem in Newtonian mechanics, but using the calculational techniques developed by Lagrange, Laplace, and others, it is possible to determine that the effects of all the other planets should contribute an additional 532 arc seconds per century to the precession of Mercury's orbit. Combined with the precession of our equinox reference line, this accounts for 5557 arc seconds per century, which is close to the observed value of 5600, but still short by 43 arc seconds per century. The astronomers assure us that their observations can't be off by more than a fraction of an arc second, so there seems to be a definite problem here.

A similar problem had appeared in the 1840's when the newly discovered planet Uranus began to deviate noticeably from the precise course that Newtonian theory prescribed. On that occasion, the astronomer Le Verrier and the mathematician Adams had (independently) inferred the existence of a previously unknown planet beyond the orbit of Uranus, and even gave instructions where it could be found. Sure enough, when that indicated region of the sky was searched by Johann Galle at the Berlin Observatory, the planet that came to be called Neptune was discovered in 1846, astonishingly close to the predicted location. This was a tremendous triumph for Le Verrier, and surely gave him confidence that all apparent anomalies in the planetary orbits could be explained on the basis of Newtonian theory, and could be used as an aid to the discovery of new celestial objects. He soon turned his attention to the anomalous precession of Mercury's orbit (which he estimated at 38 arc seconds per century, somewhat less than the modern value), and suggested that it must be due to some previously unknown mass near the Sun, possibly a large number of small objects, or perhaps even another planet, inside the orbit of Mercury.

At one point there were reports that a small planet orbiting very near the Sun had actually been sighted, and it was named Vulcan, after the Roman God of fire. Le Verrier became convinced that the new planet existed, but subsequent attempts to observe the hypothetical planet failed to find any sign of it. Even the original sightings were cast into doubt, since they had been made by an amateur, and other astronomers reported that they had been observing the Sun at the very same time and had seen nothing. Another popular theory to explain Mercury's anomalous precession, championed by the astronomer Hugo von Seeliger, was that the small particles of matter that cause the "zodiacal light" might alter the gravitation field enough to create the precession, although Simon Newcomb argued that if there were enough matter to affect Mercury's orbit so significantly there would also be enough to cause other effects on the orbits of the inner planets − effects which are not observed. Similar inconsistencies undermined the “Vulcan” hypothesis.

The failure to arrive at a realistic Newtonian explanation for the anomalous precession led some researchers, notably Asaph Hall and Simon Newcomb, to consider the possibility that Newtonian theory itself was at fault, i.e., that perhaps gravity isn't exactly an inverse square law. Hall noted that he could account for Mercury's precession if the law of gravity, instead of falling off as 1/r², actually falls of as 1/rⁿ where the exponent n is 2.00000016. However, most people didn't (and still don't) find that idea to be very appealing, since it conflicts with basic conservation laws, e.g., Gauss's Law, unless we also postulate a correspondingly modified metric for space (ironically enough). Several researchers attempted to explain Mercury’s precession by imposing a finite speed of gravity on Newton’s theory, but these efforts too gave unsatisfactory results. (See Section 8.10.)

Another possible contributor to planetary precession is oblateness of the Sun. The surface of the Sun appears to rotate about once every 25 days, and if the interior rotates at roughly the same rate, ordinary dynamics implies that the Sun would have an equatorial bulge of only about 1 part per million. This small deviation from perfect sphericity would contribute only a few hundredths of an arcsecond per century to the Newtonian prediction for the precession rate of Mercury’s orbit. There has, however, been some controversy about this conclusion. In 1966 Dicke and Goldenberg reported, based on optical measurements, that the Sun's equatorial bulge is about 50 parts per million, which would add a significant amount (about 3.4 arcseconds per century) to the Newtonian prediction. (The Brans-Dicke theory of gravity has a free parameter that could be tuned to accommodate this extra contribution.) However, those measurements were contradicted by a number of other heliometric measurements, all showing that the solar axes differ by no more than about 4 parts per million. Moreover, all such optical measurements were called into question due to variations in brightness on the Sun’s surface. More recent analyses of the Sun’s vibrational modes has shown that the interior is rotating at roughly the same rate as the surface, so there is no plausible mechanism for the oblateness to exceed about 1 part per million. Hence the current consensus is that the Sun is not nearly oblate enough to significantly affect the Newtonian prediction.

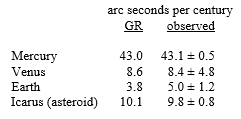
Mercury isn't the only object in the solar system that exhibits anomalous precession. The effect is most noticeable for objects near the Sun with highly elliptical orbits, but it can be seen even in the nearly circular orbits of Venus and Earth, although the discrepancy isn't nearly so large as for Mercury. In addition, the asteroid Icarus is useful for studying this effect, because it has an extremely elliptical orbit and periodically passes very close to the Sun. The table below shows the anomalous precession of four objects in the inner solar system, based on direct observations:

The large tolerances for Venus and Earth are mainly due to the fact that their orbits are so nearly circular, making it difficult to precisely determine the axes of their elliptical orbits. Incidentally, Icarus periodically crosses the Earth's path, and has actually passed within a million kilometers of us, less than 3 times the distance to the Moon. It's about 1 mile in diameter, and may eventually collide with the Earth − reason enough to keep an eye on its precession.

One hope that Einstein had throughout the time he was working on the general theory was that it would explain the anomalous precession of Mercury. Of course, as we've seen, "explanations" of this phenomenon were never in short supply, but none of them were very compelling, all seeming to be ad hoc. In contrast, Einstein found that the extra precession arises unavoidably from the fundamental principles of general relativity.

Before we derive the relativistic prediction, it’s useful to review the corresponding Newtonian calculation. By direct integration of the Newtonian inverse-square force law equated to the acceleration, we find that the Newtonian kinetic energy of a test particle of unit mass is v²/2 and the potential energy is −m/r where m is the mass of the central gravitating body (in geometrical units so G = c = 1). The sum of these is the constant energy E of the orbit (which is negative for bound orbits). Thus, noting that v² = (dr/dt)² + (ωr)², where ω = dϕ/dt is the angular velocity of the particle, we have the Newtonian equation of motion

Recalling that the angular momentum h = ωr² is constant, this can be written as

It’s convenient to re-write this equation in terms of the reciprocal radius variable u = 2m/r. Now, multiplying together the two relations du/dϕ = −(2m/r²)dr/dϕ and h = (dϕ/dt)r² we have dr/dt = −(h/(2m))du/dϕ, and so the Newtonian equation of motion in terms of the variable u is

Letting u₁ and u₂ denote the values of u at the perigee and apogee respectively, we know du/dϕ = 0 at both of these values, so they are the roots of the right hand side of this equation, and hence the equation can be written as

Now, for any given values of u₁ and u₂ (the maximum and minimum values of u), let us define a new variable α related to u implicitly by

where

It follows that u ranges from u₁ to u₂ as α ranges from 0 to π. Also note that

Making these substitutions into equation (3) and simplifying, we get dα/dϕ = ±1, and hence we can take α = ϕ in equation (4) to give the Newtonian solution, which has no precession, i.e., the angular travel between apogee and perigee is exactly π. Noting that μ = 2m/L where L denotes the harmonic mean of r₁ = 2m/u₁ and r₂ = 2m/u₂, we can revert back to the radial parameter and write the Newtonian solution (4) as

which is the familiar equation of an ellipse with no precession. The parameter L is called the semi-latus rectum of the ellipse. By the way, we could have arrived at this same result by differentiating (2) again with respect to ϕ, and dividing through by 2(du/dϕ) to give d²u/dϕ² + u = 2(m/h)², which has the form of a simple harmonic oscillator with unit frequency and solution (4) with α = ϕ.

Now we will derive the relativistic prediction for the precession of a bound orbit in a spherically symmetrical field. Beginning with the Schwarzschild metric derived in Section 6.1 from the field equations, we will work in the single plane θ = π/2, so the differential of θ vanishes, and we have sin(θ) = 1. Thus the term involving θ in the Schwarzschild metric drops out, leaving just

The Christoffel symbols and the equations of geodesic motion for this metric were already given in Section 5.5. Omitting the θ parameter, the geodesic equations are

We can immediately integrate equations (7) and (9) to give

where k and h are constants of integration, determined by the initial conditions of the orbit. Substituting for these derivatives into the basic Schwarzschild metric (6) divided by (dτ)² gives

Solving for (dr/dτ)², we have

If we identify the constant (k² – 1)/2 with the constant energy E, this equation differs from the Newtonian equation (1) only by the first term on the right hand side. (Of course, the derivative here is with respect to the proper time τ, rather than Newton’s absolute coordinate time t.) We again define u = 2m/r and make use of the relation dϕ/dτ = h/r² to arrive at the relativistic equation

which is identical to the Newtonian equation (2) except for the term u³ on the right hand side. Just as in the Newtonian case we can let u₁ and u₂ denote the values of u at the perigee and apogee respectively, and now we let u₃ denote the third root of the cubic on the right hand side, and we write this equation as

Again we define the parameters μ and ε and the variable α in terms of u₁, u₂, and u by equation (4). Also, since the negative coefficient of the second highest degree term of a monic polynomial equals the sum of the roots, we have u₃ = 1 – (u₁ + u₂) = 1 – 2μ. Making these substitutions into (12) and simplifying, we get

Therefore, the angular travel between perigee and apogee is given (exactly) by the integral

Expanding the integrand into a power series, we have

Integrating term by term, and recalling that μ = 2m/L, we get

The angular travel from one perigee to the next is twice this amount, and this exceeds 2π by

This is the precession per revolution. To the lowest order of approximation it gives the familiar result 6πm/L, independent of eccentricity. At the next order of approximation, the eccentricity does affect the result, although for realistic orbits in the solar system the quantity (m/L)² is so small that this and all higher order terms are completely imperceptible. The mass m of the Sun in geometrical units is only about 1475 meters, whereas the radius of the Sun itself is (6.95)10⁸ meters, so the second-order relativistic correction will be at least five orders of magnitude smaller than the first-order correction − which itself is extremely small.

The semi-latus rectum L of an ellipse with eccentricity ε is related to the semi-major axis “a” by L = a(1−ε²), and Kepler’s third law gives m = (2π/T)²a³ where T is the orbital period (Schwarzschild coordinate time), so the lowest-order approximation for the relativistic precession per orbit can expressed as

This sometimes misleads people into thinking that the lowest order approximation includes an effect due to the eccentricity, but in fact the eccentricity appears in this formula only to convert the semi-latus rectum to the semi-major axis.

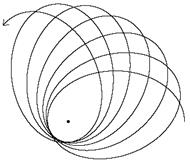
As we’ve seen, for small values of m/L the orbit is very nearly a Keplerian ellipse, but the axis of the ellipse precesses slightly, as illustrated below for an extreme case where the perihelion is at only 200m (which could not occur in our solar system because the Sun's spatial radius is much greater than 200m).

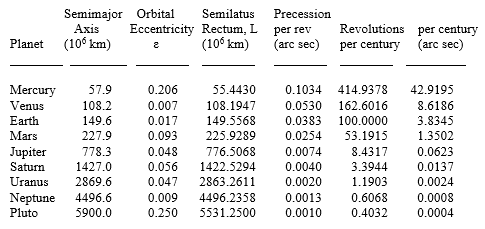
Based on the elements of the planetary orbits we can construct the following table of relativistic precession.

The observed precession of 43.1 ± 0.5 arc seconds per century for the planet Mercury is in close agreement with the theory. We noted in Section 5.8 how Einstein proudly concluded his presentation of the vacuum field equations in his 1916 paper on general relativity by pointing out that they explained the anomalous precession of Mercury. He returned to this subject at the end of the paper, giving the precession formula and closing his masterpiece with the words

Calculation gives for the planet Mercury a rotation of the orbit of 43" per century, corresponding exactly to the astronomical observation (Leverrier); for the astronomers have discovered in the motion of the perihelion of this planet, after allowing for disturbances by the other planets, an inexplicable remainder of this magnitude.

One might wonder why, in our derivation of the relativistic orbital precession, we apparently made use of only two of the three geodesic equations. This is due to the one degree of redundancy between the geodesic equations and the metric, as explained in Appendix 6.

We mentioned previously that the small eccentricities of Venus and Earth make it difficult to determine their lines of apsides with precision, but modern measurement techniques (including the use of interplanetary space probes and radar ranging) and computerized analysis of the data have enabled the fitting of the entire solar system to a parameterized post-Newtonian (PPN) model that encompasses a fairly wide range of theories (including general relativity). Once the parameters of this model have been fit to all the available data for the Sun and planets, the model can then be used to compute the "best observational fit" for the precessions of the individual planets based on the PPN formalism. This gives precessions (in excess of the Newtonian predictions) of 43.1, 8.65, 3.85, and 1.36 arcseconds per century for the four inner planets respectively, in remarkable agreement with the predictions of general relativity.

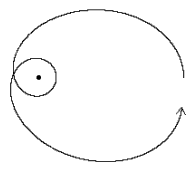
If we imagine an extremely dense central object, whose mass is concentrated inside it's gravitational radius, we can achieve much greater deviations from conventional Newtonian orbits. For example, if the precession rate is roughly equal to the orbital rate, we have an orbit as shown below:

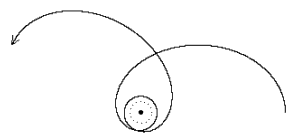
For an orbit with slightly less energy the path looks like this:

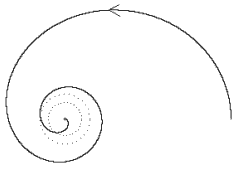
where the dotted circle signifies the "light orbit" radius r = 3m. With sufficient angular momentum it's possible to arrange for persistent timelike orbits periodically descending down to any radius greater than 3m, which is the smallest possible radius of a circular orbit (but note that a circular orbit with radius less than 6m is unstable). If a timelike geodesic ever passes inside that radius it must then spiral in to the central mass, as illustrated below.

Here the outer dotted circle is at 3m, and the inner circle is at the event horizon, 2m. Once a worldline has fallen within 2m, whether geodesic or not, it's radial coordinate must (according to the Schwarzschild solution) thereafter decrease monotonically to zero. (The periodic solution derived previously does not apply to these solutions, because they do not include two events at which dr/dθ = 0.)

Regarding these spiral solutions there is an ironic historical precedent. A few years before writing the Principia Newton once described in a letter to Robert Hooke the descent of an object along a spiral path to the center of a gravitating body. Several years later, after the Principia had established Newton's reputation, the two men became engaged in a bitter priority dispute over the discovery of universal gravitation, and Hooke used this letter as evidence that Newton hadn't understood gravity at that time, because the classical inverse-square law of gravity permits no such spiral solutions. Newton replied that it had simply been a "negligent stroke with his pen". Interestingly, although people sometimes credit Newton with originating the idea of photons based on his erroneous corpuscular theory of light, it's never been suggested that his "negligent spiral" was a premonition of the Schwarzschild solution of Einstein's field equations.

Return to Table of Contents